Clase 11 Soluciones RD Sharma – Capítulo 26 Elipse – Ejercicio 26.1

Pregunta 11. Encuentra la ecuación de la elipse cuyos focos están en (±3, 0) y que pasa por (4, 1).

Solución:

Sea la ecuación de la elipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Dado que la elipse cuyos focos están en (±3, 0) y que pasa por (4, 1)

Asi que,

ae = 3

(ae) ² = 9

y = 1 y x = 4

Sustituyendo los valores de x e y en la ecuación anterior, tenemos:

$\frac{16}{a^2}+\frac{1}{b^2}=1$ …(ii)

Como sabemos que, b ² = a ² (1 – e ² )

⇒ ^{segundo 2} = un ² – un ² mi ²

⇒ ^{segundo 2} = un ² – 9

o

a ² = b ² + 9 ….(iii)

Al resolver la ecuación (ii), obtenemos

16b ² + un ² = un ² segundo ²

Ahora pon el valor de a ² de la ecuación (iii), obtenemos

16b ² + b ² + 9 = (b ² + 9)b ²

b ⁴ – 8b ² – 9 = 0

⇒ b = ±3

Entonces, a = 3√2

Ahora ponga el valor de a ² y b ² en eq(i), obtenemos

$\frac{x^2}{18}+\frac{y^2}{9}=1$

Por lo tanto, $\frac{x^2}{18}+\frac{y^2}{9}=1$ es la ecuación requerida.

Pregunta 12. Halla la ecuación de una elipse cuya excentricidad es 2/3, el latus rectum es 5 y el centro es el origen.

Solución:

Sea la ecuación de la elipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ …..(i)

Dado que

excentricidad(e) = 2/3

lado recto = 5

Entonces, 2b ² /a = 5 …..(ii)

⇒ 2b ² = 5a

⇒ 10a ² = 45a

⇒ un = 9/2

Al sustituir el valor de a en la ecuación (ii), tenemos:

⇒ ^{segundo 2} = 45/4

Ahora ponga el valor de a ² y b ² en eq(i), obtenemos

$\frac{4x^2}{81}+\frac{4y^2}{45}=1$

Por lo tanto, $\frac{4x^2}{81}+\frac{4y^2}{45}=1$ es la ecuación de la elipse.

Pregunta 13. Encuentra la ecuación de la elipse con sus focos en el eje y, la excentricidad es 3/4, centro en el origen y que pasa por (6, 4).

Solución:

Sea la ecuación del plano $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

Dado que

excentricidad(e) = 3/4,

Como sabemos que a ² = b ² (1 – e ² )

⇒ $a^2=b^2(1-\frac{9}{16})$

⇒ $a^2=\frac{7}{16}b^2$

⇒ $\frac{x^2}{a^2}+\frac{7y^2}{16a^2}=1$

Como pasa por (6,4), tenemos:

⇒ $\frac{36}{a^2}+\frac{112}{16a^2}=1$

⇒ a ² = 43 y b ² = 688/7

Ahora ponga el valor de a ² y b ² en eq(i), obtenemos

$\frac{x^2}{43}+\frac{7y^2}{688}=1$

Así $\frac{x^2}{43}+\frac{7y^2}{688}=1$ es la ecuación requerida.

Pregunta 14. Encuentra la ecuación de la elipse cuyos ejes se encuentran a lo largo de ejes de coordenadas y que pasa por (4, 3) y (-1, 4).

Solución:

Sea la ecuación de la elipse: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Se da que la elipse pasa por (4, 3) y (-1, 4).

⇒ $\frac{16}{a^2}+\frac{9}{b^2}=1$ y $\frac{1}{a^2}+\frac{16}{b^2}=1$

dejar $p=\frac{1}{a^2}$ y $r=\frac{1}{b^2}$

Entonces, 16p + 9r = 1 y p + 16b = 1

Al resolver estas ecuaciones tenemos:

$p=\frac{1}{a^2}=\frac{7}{247}$ y $r=\frac{1}{b^2}=\frac{15}{247}$

Ahora, sustituyendo todos los valores en la ecuación (i), tenemos:

$\frac{7x^2}{247}+\frac{15y^2}{247}=1$

Por lo tanto , $\frac{7x^2}{247}+\frac{15y^2}{247}=1$ es la ecuación requerida.

Pregunta 15. Encuentra la ecuación de una elipse cuyos ejes se encuentran a lo largo de los ejes de coordenadas, que pasa por el punto (-3, 1) y tiene una excentricidad igual a 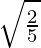$\sqrt{\frac{2}{5}}$ .

Solución:

Sea la ecuación de la elipse: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ……(i)

Se da que la elipse pasa por el punto (-3, 1).

Asi que,

⇒ $\frac{9}{a^2}+\frac{1}{b^2}=1$

Como sabemos que b ² = a ² (1 – e ² )

También la excentricidad(e) = $\sqrt{\frac{2}{5}}$ .

⇒ ^{segundo 2} = un ² (1 – 2/5)

⇒ ^{segundo 2} = 3a ² /5

Al sustituir los valores, tenemos:

$\frac{9}{a^2}+\frac{5}{3a^2}=1$

⇒ un ² = 32/2

⇒ ^{segundo 2} = 32/5

Ahora ponga el valor de a ² y b ² en eq(i), obtenemos

$\frac{x^2}{\frac{32}{2}}+\frac{y^2}{\frac{32}{5}}=1$

Por lo tanto , 3x ² + 5y ² = 32 es la ecuación requerida.

Pregunta 16. Encuentra la ecuación de la elipse, la distancia entre los focos es de 8 unidades y la distancia entre las directrices es de 18 unidades.

Solución:

Sea la ecuación de la elipse: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ……(i)

Dado que la distancia entre focos = 8 unidades

Entonces, 2ae = 8 …(i)

Distancia entre directrices = 18 unidades

Entonces, 2a/e = 18 …(i)

De la ecuación (i) y (ii), obtenemos

⇒ mi = 8/2a

⇒ 4a ² = 18(8)

⇒ un ² = 36

⇒ un = 6

⇒ mi = 2/3

Ahora, b ² = a ² (1 – e ² )

⇒ ^{segundo 2} = 36(1 – 4/9)

⇒ ^{segundo 2} = 36(5/9)

⇒ ^{segundo 2} = 20

Ahora ponga los valores de a ² y b ² en eq(i), obtenemos

$\frac{x^2}{36}+\frac{y^2}{20}=1$

Por lo tanto, $\frac{x^2}{36}+\frac{y^2}{20}=1$ es la ecuación requerida.

Pregunta 17. Encuentra la ecuación de la elipse cuyos vértices son (0, ±10) y la excentricidad es 4/5.

Solución:

Sea la ecuación de la elipse: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ …..(i)

Como sabemos que los vértices de la elipse están en el eje y, las coordenadas de los vértices son (0, ±10).

Por lo tanto, b = 10

Ya que, a ² = b ² (1 – e ² )

excentricidad(e) = 4/5 (dado)

⇒ un ² = 100(1 – (4/5) ² )

⇒ un ² = 100(1 – 16/25)

⇒ un ² = 36

Ahora ponga los valores de a ² y b ² en eq(i), obtenemos

$\frac{x^2}{36}+\frac{y^2}{100}=1$

Por lo tanto, 100x ² + 36y ² =3600 es la ecuación requerida.

Pregunta 18. Una barra de 12 m de longitud se mueve con sus extremos tocando los ejes de coordenadas. Determine la ecuación del lugar geométrico de un punto P en la barra, que está a 3 cm del extremo en contacto con el eje x.

Solución:

Consideremos AB la barra que forma un ángulo θ con la recta OX y sea P(x, y) el punto sobre ella tal que AP = 3 cm.

Entonces, PB = AB – AP = 12 – 3 = 9 cm

De este modo, $cosθ=\frac{PQ}{PB}=\frac{x}{9}$

y, $sinθ=\frac{PR}{PA}=\frac{y}{3}$

Como sabemos que sen ² θ + cos ² θ = 1, tenemos:

$(\frac{y}{3})^2+(\frac{x}{9})^2=1$

Por tanto $\frac{x^2}{81}+\frac{y^2}{9}=1$ , es el lugar geométrico del punto P.

Pregunta 19. Encuentra la ecuación del conjunto de todos los puntos cuyas distancias desde (0, 4) son dos tercios de sus distancias desde la línea y = 9.

Solución:

Dado que PQ = 2/3PL

Asi que,

⇒ $\sqrt{(x-0)^2+(y-4)^2}=\frac{2}{3}(y-9)$

⇒ 3 ² [x ² + (y – 4) ² ] = 2 ² (y – 9) ²

⇒ 9x ² + 9y ² – 72y + 144 = 4y ² – 72y + 324

⇒ 9×2 ⁺ 5y2 ⁼ 180

Así $\frac{x^2}{20}+\frac{y^2}{36}=1$ es la ecuación requerida.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 26 Elipse – Ejercicio 26.1 | conjunto 2

Pregunta 11. Encuentra la ecuación de la elipse cuyos focos están en (±3, 0) y que pasa por (4, 1).

Pregunta 12. Halla la ecuación de una elipse cuya excentricidad es 2/3, el latus rectum es 5 y el centro es el origen.

Pregunta 13. Encuentra la ecuación de la elipse con sus focos en el eje y, la excentricidad es 3/4, centro en el origen y que pasa por (6, 4).

Pregunta 14. Encuentra la ecuación de la elipse cuyos ejes se encuentran a lo largo de ejes de coordenadas y que pasa por (4, 3) y (-1, 4).

Pregunta 15. Encuentra la ecuación de una elipse cuyos ejes se encuentran a lo largo de los ejes de coordenadas, que pasa por el punto (-3, 1) y tiene una excentricidad igual a $\sqrt{\frac{2}{5}}$ .

Pregunta 16. Encuentra la ecuación de la elipse, la distancia entre los focos es de 8 unidades y la distancia entre las directrices es de 18 unidades.

Pregunta 17. Encuentra la ecuación de la elipse cuyos vértices son (0, ±10) y la excentricidad es 4/5.

Pregunta 18. Una barra de 12 m de longitud se mueve con sus extremos tocando los ejes de coordenadas. Determine la ecuación del lugar geométrico de un punto P en la barra, que está a 3 cm del extremo en contacto con el eje x.

Pregunta 19. Encuentra la ecuación del conjunto de todos los puntos cuyas distancias desde (0, 4) son dos tercios de sus distancias desde la línea y = 9.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Encuentra la ecuación de la elipse cuyos focos están en (±3, 0) y que pasa por (4, 1).

Pregunta 12. Halla la ecuación de una elipse cuya excentricidad es 2/3, el latus rectum es 5 y el centro es el origen.

Pregunta 13. Encuentra la ecuación de la elipse con sus focos en el eje y, la excentricidad es 3/4, centro en el origen y que pasa por (6, 4).

Pregunta 14. Encuentra la ecuación de la elipse cuyos ejes se encuentran a lo largo de ejes de coordenadas y que pasa por (4, 3) y (-1, 4).

Pregunta 15. Encuentra la ecuación de una elipse cuyos ejes se encuentran a lo largo de los ejes de coordenadas, que pasa por el punto (-3, 1) y tiene una excentricidad igual a .

Pregunta 16. Encuentra la ecuación de la elipse, la distancia entre los focos es de 8 unidades y la distancia entre las directrices es de 18 unidades.

Pregunta 17. Encuentra la ecuación de la elipse cuyos vértices son (0, ±10) y la excentricidad es 4/5.

Pregunta 18. Una barra de 12 m de longitud se mueve con sus extremos tocando los ejes de coordenadas. Determine la ecuación del lugar geométrico de un punto P en la barra, que está a 3 cm del extremo en contacto con el eje x.

Pregunta 19. Encuentra la ecuación del conjunto de todos los puntos cuyas distancias desde (0, 4) son dos tercios de sus distancias desde la línea y = 9.

Deja una respuesta Cancelar la respuesta

Pregunta 15. Encuentra la ecuación de una elipse cuyos ejes se encuentran a lo largo de los ejes de coordenadas, que pasa por el punto (-3, 1) y tiene una excentricidad igual a $\sqrt{\frac{2}{5}}$ .