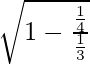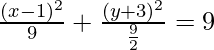Clase 11 Soluciones RD Sharma – Capítulo 26 Elipse – Ejercicio 26.1

Pregunta 1. Encuentra la ecuación de la elipse cuyo foco es (1,–2) y la directriz es 3x – 2y + 5 = 0, y la excentricidad es 1/2.

Solución:

Dado que,

El foco es (1, -2)

la directriz es 3x – 2y + 5 = 0,

la excentricidad (e) es 1/2.

Como sabemos, SP = ePM

⇒ SP = PM/2

⇒ (SP) ² = 1/4 (PM) ²

⇒ 4(SP) ² = (PM) ²

⇒ 4[(x – 1) ² + (y + 2) ² ] = $[\frac{3x-2y+5}{\sqrt{3^2+2^2}}]^2$

⇒ 4[x ² + 1 – 2x + y ² + 4 + 4y] = $\frac{(3x-2y+5)^2}{13}$

⇒ 52[x ² + 1 – 2x + y ² + 4 + 4y] = (3x – 2y + 5) ²

⇒ 52[x ² + 1 – 2x + y ² + 4 + 4y] = 9x ² + 4y ² + 25 – 12xy – 20y + 30x

Por lo tanto, 43x ² + 43y ² + 12xy – 134x + 228y + 235 = 0 es la ecuación requerida.

Pregunta 2. Encuentra la ecuación de la elipse si:

(i) El foco es (0, 1), la directriz es x + y = 0 y e = 1/2.

Solución:

Dado que,

el foco es (0, 1),

directriz es x + y = 0

la excentricidad (e) es 1/2

Como sabemos, SP = ePM

⇒ SP = PM/2

⇒ (SP) ² = 1/4 (PM) ²

⇒ 4(SP) ² = (PM) ²

⇒ 4[(x – 0) ² + (y – 1) ² ] = $[\frac{x+y}{\sqrt{1^2+1^2}}]^2$

⇒ 8[x ² + y ² – 2y + 1] = x ² + y ² + 2xy

Por lo tanto, 7x ² + 7y ² – 2xy – 16y + 8 = 0 es la ecuación requerida.

(ii) El foco es (–1,1), la directriz es x – y + 3 = 0 ye = 1/2.

Solución:

Dado que,

el foco es (-1, 1),

directriz es x – y + 3 = 0

la excentricidad (e) es 1/2

Como sabemos, SP = ePM

⇒ SP = PM/2

⇒ (SP) ² = 1/4 (PM) ²

⇒ 4(SP) ² = (PM) ²

⇒ 4[(x + 1) ² + (y – 1) ² ] = $[\frac{x-y+3}{\sqrt{1^2+1^2}}]^2$

⇒ 4[(x + 1) ² + (y – 1) ² ] = (x – y + 3) ² /2

⇒ 8[(x + 1) ² + (y – 1) ² ] = (x – y + 3) ²

⇒ 8[(x + 1) ² + (y – 1) ² ] = x ² + y ² + 9 – 6y – 2xy + 6x

⇒ 8[(x ² + 1 + 2x)+ (y ² + 1 – 2y)] = x ² + y ² + 9 – 6y – 2xy + 6x

⇒ 8[x ² + y ² + 2 + 2x – 2y] = x ² + y ² + 9 – 6y – 2xy + 6x

Por lo tanto, 7x ² + 7y ² + 2xy + 10x – 10y + 7 = 0 es la ecuación requerida.

(iii) El foco es (–2,3), la directriz es 2x + 3y + 4 = 0 y e = 4/5.

Solución:

Dado que,

el foco es (-2, 3),

directriz es 2x + 3y + 4 = 0

la excentricidad (e) es 4/5

Como sabemos, SP = ePM

⇒ SP = 4/5 (PM)

⇒ (SP) ² = 16/25 (PM) ²

⇒ 25 (SP) ² = 16 (PM) ²

⇒ 25[(x + 2) ² + (y – 3) ² ] = $16[\frac{2x+3y+4}{\sqrt{2^2+3^2}}]^2$

⇒ 25[(x + 2) ² + (y – 3) ² ] = 16(2x + 3y + 4 ⁾ 2/13

Por lo tanto, 325[x ² + y ² + 4x – 6y + 13] = 16(2x + 3y + 4) ² es la ecuación requerida.

(iv) El foco es (1, 2), la directriz es 3x + 4y – 5 = 0 y e = 1/2.

Solución:

Dado que,

el foco es (1, 2),

directriz es 3x + 4y – 5 = 0

la excentricidad (e) es 1/2

Sabemos, SP = ePM

⇒ SP = PM/2

⇒ (SP) ² = 1/4 (PM) ²

⇒ 4(SP) ² = (PM) ²

⇒ 4[(x – 1) ² + (y – 2) ² ] = $[\frac{3x+4y-5}{\sqrt{3^2+4^2}}]^2$

⇒ 4[(x – 1) ² + (y – 2) ² ] = (3x + 4y – 5) ² /25

⇒ 100[(x – 1) ² + (y – 2) ² ] = 9x ² + 16y ² + 25 + 24xy – 40y – 30x

⇒ 100[(x ² + 1 – 2x) + (y ² + 4 – 4y)] = 9x ² + 16y ² + 25 + 24xy – 40y – 30x

Por lo tanto, 91x ² + 84y ² – 24xy – 170x – 360y + 475 = 0 es la ecuación requerida.

Pregunta 3. Encuentra la excentricidad, las coordenadas de los focos, la longitud del latus-rectum de la elipse:

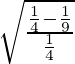
(yo) 4x ² + 9y ² = 1

Solución:

Dado que 4x ² + 9y ² = 1

$\frac{x^2}{\frac{1}{4}}+\frac{y^2}{\frac{1}{9}}=1$

Asi que,

⇒ Excentricidad = $\sqrt{\frac{\frac{1}{4}-\frac{1}{9}}{\frac{1}{4}}}$

= √5/3

Longitud del latus rectum = $\frac{\frac{2}{9}}{\frac{1}{2}}$

= 4/9

Los focos son (√5/6; 0) y (-√5/6; 0)

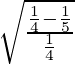
(ii) 5x ² + 4y ² = 1

Solución:

Dado que 5x ² + 4y ² = 1

$\frac{x^2}{\frac{1}{5}}+\frac{y^2}{\frac{1}{4}}=1$

Asi que,

⇒ Excentricidad = $\sqrt{\frac{\frac{1}{4}-\frac{1}{5}}{\frac{1}{4}}}$

= 1/√5

Longitud del latus rectum = $\frac{\frac{2}{5}}{\frac{1}{2}}$

= 4/5

Los focos son (0; 1/2√5) y (0; -1/2√5)

(iii) 4x ² + 3y ² = 1

Solución:

Dado que 4x ² + 3y ² = 1

$\frac{x^2}{\frac{1}{4}}+\frac{y^2}{\frac{1}{3}}=1$

Asi que,

⇒ Excentricidad = $\sqrt{1-\frac{\frac{1}{4}}{\frac{1}{3}}}$

= 1/2

Longitud del latus rectum = 2a ² /b

= $\frac{\frac{2}{4}}{\frac{1}{\sqrt3}}$

= √3/2

Los focos son (0; 1/2√3) y (0; -1/2√3).

(iv) 25x ² + 16y ² = 1600

Solución:

Dado que 25x ² + 16y ² = 1600

$\frac{25x^2}{1600}+\frac{16y^2}{1600}=1$

⇒ $\frac{25x^2}{1600}+\frac{16y^2}{1600}=1$

Asi que,

⇒ Excentricidad = $\sqrt{1-\frac{a^2}{b^2}}$

= 3/5

⇒ Las coordenadas de los focos son (0, 6) y (0, –6).

⇒ Longitud del latus rectum = 2a ² /b

= 2 × (64/10)

= 64/5

(v) 9x ² + 25y ² = 225

Solución:

Dado que 9x ² + 25y ² = 225

=> \frac{9x^2}{225}+\frac{25y^2}{225}=1

=> $\frac{x^2}{25}+\frac{y^2}{9}=1$

Claramente, a = 5 y b = 3.

Asi que,

⇒ Excentricidad = $\sqrt{1-\frac{3^2}{5^2}}$

= 4/5

⇒ Las coordenadas de los focos son (4, 0) y (–4, 0).

⇒ Longitud del latus rectum = 2b ² /a

= 2 × (9/5)

= 18/5

Pregunta 4. Encuentra la ecuación de la elipse que pasa por el punto (–3, 1) y tiene excentricidad $\sqrt{\frac{2}{5}}$ .

Solución:

Sea la ecuación del plano:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ …(i)

Se da que la elipse pasa por el punto (–3, 1), entonces,

$\frac{9}{a^2}+\frac{1}{b^2}=1$ …(ii)

⇒ $e=\sqrt{1-\frac{a^2}{b^2}}$

⇒ $\sqrt{\frac{2}{5}}=\sqrt{1-\frac{a^2}{b^2}}$

⇒ b ² /a ² = 3/5

⇒ ^{segundo 2} = 3a ² /5

⇒ b ² = 3a ² /5 ……(iii)

Ahora pon el valor de b ² en la ecuación (ii), obtenemos

$\frac{9}{a^2}+\frac{1}{\frac{3a^2}{5}}=1$

$\frac{9}{a^2}+\frac{5}{3a^2}=1$

$\frac{1}{a^2}[9 + \frac{5}{3}]=1$

9 + 5/3 = un ²

un ² = 32/3

Ahora ponga el valor w de a ² en la ecuación (iii), obtenemos,

b ² = 3/5 x 32/3 = 32/5

Ahora ponga a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{\frac{32}{3}}+\frac{y^2}{\frac{32}{5}}=1$

Por lo tanto, 3x ² + 5y ² = 32 es la ecuación requerida del plano.

Pregunta 5. Encuentra la ecuación de la elipse si:

(i) e = 1/2 y focos (±2, 0).

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ …(i)

Ahora, ae = 2

o, un ² = 16

Ahora, b ² = a ² (1 – e ² )

⇒ ^{segundo 2} = 16(1 – (1/2) ² )

⇒ ^{segundo 2} = 12

Ahora ponga a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{16}+\frac{y^2}{12}=1$

Así 3x ² + 4y ² = 48 es la ecuación de la elipse.

(ii) e = 2/3 y longitud de latus-rectum = 5

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ …(i)

Ahora,

⇒ 2b ² /a = 5

⇒ b ² = 5a/2 ….(ii)

Ya que, b ² = a ² (1 – e ² )

⇒ 5a/2 = un ² (1 – (2/3) ² )

⇒ un = 9/2

⇒ un ² = 81/4

Ahora ponga el valor de a en la ecuación (ii), obtenemos

b ² = 5/2 x 9/2

b2 ⁼ 45/4

Ahora ponga a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{\frac{81}{4}}+\frac{y^2}{\frac{45}{4}}=1$

Por lo tanto, 20x ² + 36y ² = 405 es la ecuación requerida.

(iii) e = 1/2 y semieje mayor = 4

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Semi – eje mayor = a = 4

⇒ un ² = 16

Sabemos, a ² = b ² (1 – e ² )

⇒ 16 = ^{segundo 2} (1 – (1 ² /2 ² ))

⇒ ^{segundo 2} = 12

Ahora ponga a ² y b ² en la ecuación (i), obtenemos,

⇒ $\frac{x^2}{16}+\frac{y^2}{12}=1$

Por lo tanto, 3x ² + 4y ² = 48 es la ecuación requerida.

(iv) e = 1/2 y eje mayor = 12

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Dado, 2a = 12

⇒ un = 6

Sabemos, $b=\sqrt{1-\frac{b^2}{a^2}}$

⇒ $\frac{1}{2}=\sqrt{1-\frac{b^2}{36}}$

⇒ ^{segundo 2} = 27

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

⇒ $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

⇒ $\frac{x^2}{36}+\frac{y^2}{27}=1$

Así 3x ² + 4y ² = 108 es la ecuación de la elipse.

(v) Pasa por (1, 4) y (–6, 1).

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Dado que la elipse pasa por (1, 4) y (–6, 1), obtenemos

$\frac{1}{a^2}+\frac{16}{b^2}=1$

Sea p = 1/a ² y r = 1/b ²

⇒ p + 16r = 1 ……(ii)

Como la elipse también pasa por el punto (–6, 1), tenemos

$\frac{36}{a^2}+\frac{1}{b^2}=1$

⇒ 36p + r = 1 ……(iii)

Al resolver las ecuaciones (ii) y (iii), tenemos:

p = 3/115; r = 7/115

Al sustituir los valores en la ecuación (i), obtenemos;

⇒ $\frac{3x^2}{115}+\frac{7y^2}{115}=1$

Por lo tanto, 3x ² + 7y ² = 115 es la ecuación requerida.

(vi) Sus vértices son (±5, 0) y focos (±4, 0)

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Dado que a = 5 y ae = 4

Por lo tanto, e = 4/5 $e=\frac{4}{5}$

Ahora, b ² = a ² (1 – e ² )

⇒ ^{segundo 2} = 25(1 – 16/25)

⇒ ^{segundo 2} = 9

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

Así $\frac{x^2}{25}+\frac{y^2}{9}=1$ es la ecuación requerida.

(vii) Los vértices son (0, ±13) y los focos (0, ±5)

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Dado: b = 13 y be = 5

Por lo tanto, e = 5/13

Ahora, a ² = b ² (1 – e ² )

⇒ un ² = 169(1 – 25/169)

⇒ un ² = 144

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{144}+\frac{y^2}{169}=1$

Así $\frac{x^2}{144}+\frac{y^2}{169}=1$ es la ecuación requerida.

(viii) Sus vértices son (±6, 0) y focos (±4, 0)

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Dado: a = 6 y ae = 4

Así, e = 2/3

Ahora, b ² = a ² (1 – e ² )

⇒ ^{segundo 2} = 36(1 – 16/36)

⇒ ^{segundo 2} = 20

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{36}+\frac{y^2}{20}=1$

Así $\frac{x^2}{36}+\frac{y^2}{20}=1$ es la ecuación requerida.

(ix) Extremos del eje mayor (±3, 0) y extremos del eje menor (0, ±2).

Solución:

Sea la ecuación de la elipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ …..(i)

Extremos del eje mayor = (±3, 0)

Extremos del eje menor = (0, ±2)

Dado que los extremos de los ejes mayor y menor son (±a, 0) y (0, ±b) respectivamente.

Por lo tanto, a = 3 y b = 2

Entonces, a ² = 9, b ² = 4

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{9}+\frac{y^2}{4}=1$

Por lo tanto, $\frac{x^2}{9}+\frac{y^2}{4}=1$ es la ecuación requerida.

(x) Extremos del eje mayor (0, ±√5) y extremos del eje menor (±1, 0).

Solución:

Sea la ecuación de la elipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Extremos del eje mayor = (0, ±√5)

Extremos del eje menor = (±1, 0)

Dado que los extremos de los ejes mayor y menor son (±a, 0) y (0, ±b) respectivamente.

Por lo tanto, a = 1 y b = √5

Entonces, a ² = 1, b ² = 5

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{1}+\frac{y^2}{5}=1$

Por lo tanto, $\frac{x^2}{1}+\frac{y^2}{5}=1$ es la ecuación requerida.

(xi) La longitud del eje mayor es 26 y los focos (±5, 0).

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Teniendo en cuenta que la longitud del eje mayor = 26 y focos (±5, 0).

Tenemos, 2a = 26

⇒ un = 13

⇒ un ² = 169

Además, ae = 5

⇒ mi = 5/13

Sabemos, $e=\sqrt{1-\frac{b^2}{a^2}}$

⇒ $\frac{5}{13}=\sqrt{1-\frac{b^2}{169}}$

⇒ ^{segundo 2} = 144

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{169}+\frac{y^2}{144}=1$

Así $\frac{x^2}{169}+\frac{y^2}{144}=1$ es la ecuación requerida.

(xii) La longitud del eje menor es 16 y los focos (0, ±6)

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Dado que, la longitud del eje menor es 16

2a = 16

un = 8

un ² = 64

Ahora las coordenadas de los focos son (0, ±be)

Entonces, ser = 6

(ser) ² = 36

Sabemos, a ² = b ² (1 – e ² )

un ² = ^{segundo 2} – ^{segundo 2} mi ²

64= ^{segundo 2} – 36

b ² = 100

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{64}+\frac{y^2}{100}=1$

Por lo tanto, $\frac{x^2}{64}+\frac{y^2}{100}=1$ es la ecuación requerida.

(xiii) Los focos son (±3, 0) y a = 4

Solución:

Sea la ecuación de la elipse:

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Dado que, ae = 3 y a = 4

Así, e = 3/4 y a ² = 16

Sabemos, $e=\sqrt{1-\frac{b^2}{a^2}}$

⇒ $\frac{3}{4}=\sqrt{1-\frac{b^2}{16}}$

⇒ ^{segundo 2} = 7

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{16}+\frac{y^2}{7}=1$

Así $\frac{x^2}{16}+\frac{y^2}{7}=1$ es la ecuación requerida de la elipse.

Pregunta 6. Encuentra la ecuación de la elipse cuyos focos son (±4, 0), e = 1/3.

Solución:

Sea la ecuación de la elipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ ….(i)

Entonces las coordenadas de los focos son (±a, 0).

Tenemos, ae = 4 y e = 1/3

Por lo tanto, a = 12

y un ² = 144

Sabemos que, b ² = a ² (1 – e ² )

⇒ ^{segundo 2} = 144(1 – (1/3) ² )

⇒ ^{segundo 2} = 144(8/9)

⇒ ^{segundo 2} = 128

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{144}+\frac{y^2}{128}=1$

Por lo tanto, $\frac{x^2}{144}+\frac{y^2}{128}=1$ es la ecuación requerida.

Pregunta 7. Encuentra la ecuación de la elipse en la forma estándar cuyo eje menor es igual a la distancia entre los focos y cuyo latus rectum es 10.

Solución:

Dado eso, las coordenadas de los focos son (±ae, 0).

2b = 2ae

⇒ b = ae

⇒ b ² = a ² e ² ….(i)

También dado que el latus rectum es 10

Entonces, 2b ² /a = 10

b ² = 5a ….(ii)

Como sabemos que b ² = a ² (1 – e ² )

⇒ ^{segundo 2} = un ² (1 – mi ² )

⇒ ^{segundo 2} = un ² – un ² mi ²

⇒ ^{segundo 2} = un ² – ^{segundo 2}

⇒ 2b ² = un ²

⇒ b ² = a ² /2 ….(iii)

Ahora ponga el valor de b ² en la ecuación (ii), obtenemos

un ² /2 = 5a

un = 10

Entonces, un ² = 100

Ahora pon el valor a ² de en la ecuación (iii), obtenemos

b2 ⁼ 100/2

b ² = 50

Al sustituir los valores de a ² y b ² en la ecuación (i), obtenemos,

$\frac{x^2}{100}+\frac{y^2}{50}=1$

Por lo tanto, x ² + 2y ² = 100 es la ecuación requerida.

Pregunta 8. Encuentra la ecuación de la elipse cuyo centro es (-2, 3) y cuyos semiejes son 3 y 2 cuando el eje mayor es (i) paralelo al eje x (ii) paralelo al eje y .

Solución:

(i) Cuando el eje mayor es paralelo al eje x

Supongamos $\frac{(x-x_1)^2}{a^2}+\frac{(y-y_1)^2}{b^2}=1$ ser la ecuación.

Entonces, al sustituir los valores x ₁ = -2, y ₁ = 3, a = 3 y b = 2 en la ecuación, tenemos:

$\frac{(x+2)^2}{9}+\frac{(y-3)^2}{4}=1$

Por lo tanto, 4x ² + 9y ² + 16x – 54y + 61 = 0 es la ecuación requerida.

(ii) Cuando el eje mayor es paralelo al eje y

Supongamos $\frac{(x-x_1)^2}{a^2}+\frac{(y-y_1)^2}{b^2}=1$ ser la ecuación.

Entonces, al sustituir los valores x ₁ = -2, y ₁ = 3, a = 2 y b = 3 en la ecuación, tenemos:

$\frac{(x+2)^2}{4}+\frac{(y-3)^2}{9}=1$

Por lo tanto, 9x ² + 4y ² + 36x – 24y + 36 = 0 es la ecuación requerida.

Pregunta 9. Encuentra la excentricidad de una elipse cuya:

(i) Latus rectum es la mitad de su eje menor

Solución:

Dado que, 2b ² /a = 2b/2

⇒ 2b ² = ab

⇒ 2b = un

Ya que, $e=\sqrt{1-\frac{b^2}{4a^2}}$

⇒ $e=\sqrt{1-\frac{1}{4}}$

⇒ e = √3/2

Por lo tanto, la excentricidad de una elipse es √3/2

(ii) Latus rectum es la mitad de su eje mayor

Solución:

Dado que, 2b ² /a = 2a/2

⇒ 2b ² = un ²

Ya que, $e=\sqrt{1-\frac{b^2}{2b^2}}$

⇒ $e=\sqrt{1-\frac{1}{2}}$

⇒ mi = 1/√2

Pregunta 10. Encuentra el centro, las longitudes de los ejes, la excentricidad, los focos de la siguiente elipse:

(i) x ² + 2y ² – 2x + 12y + 10 = 0

Solución:

Dado que x ² + 2y ² – 2x + 12y + 10 = 0

(x2 – ^2x ) + 2( ^y2 + 6y) = -10

⇒ (x2 – ^2x + 1) + 2( ^y2 + 6y + 9) = -10 + 18 + 1

⇒ $\frac{(x-1)^2}{9}+\frac{(y+3)^2}{\frac{9}{2}}=9$

Entonces, x ₁ = 1, y ₁ = -3

y a = 3 y b = 3/√2

Centro = (1, -3)

Eje mayor = 2a = 2(3) = 6

Eje menor = 2b = 3\sqrt2

e= $\sqrt{1-\frac{b^2}{a^2}}$

= 1/√2

Focos = (1 ± 3/√2; -3)

(ii) x ² + 4y ² – 4x + 24y + 31 = 0

Solución:

Dado que x ² + 4y ² – 4x + 24y + 31 = 0

(x2 – 4x) + 4( ^y2⁺ 6y) = -31

⇒ (x2 – 4x + 4) + 4( ^y2⁺ 6y + 9) = 9

⇒ $\frac{(x-1)^2}{9}+\frac{(y+3)^2}{\frac{9}{2}}=9$

Entonces, x ₁ = 1, y ₁ = -3

y a = 3 y b = 3/2

Centro = (2, -3)

Eje mayor = 2a = 2(3) = 6

Eje menor = 2b = 3

e= $\sqrt{1-\frac{b^2}{a^2}}$

= √3/2

Focos = (2 ± 3/√2; -3)

(iii) 4x ² + y ² – 8x + 2y +1 = 0

Solución:

Dado que 4x ² + y ² – 8x + 2y +1 = 0

4(x2 – ^2x ) + ( ^y2 + 2y) = -1

4(x2 – ^2x + 1) + ( ^y2 + 2y + 1) = -1 + 4 + 1

4(x ² – 1) + (y ² + 1) = 4

⇒ $\frac{(x-1)^2}{1}+\frac{(y+1)^2}{4}=1$

Entonces, x ₁ = 1, y ₁ = -1

y a = 1 y b = 2

Centro = (1,-1)

Eje menor = 2a = 2(1) = 2

Eje menor = 2b = 4

mi = $\sqrt{1-\frac{b^2}{a^2}}$

e = √3/2

Focos = (1, -1 ± √3)

(iv) 3x ² + 4y ² – 12x – 8y + 4 = 0

Solución:

Dado que 3x ² + 4y ² – 12x – 8y + 4 = 0

3(x2 – 4x) + 4( ^y2^– 2y) = -4

3(x2 – 4x + 4) + 4( ^y2^– 2y + 1) = -4 + 12 + 4

⇒ $\frac{(x-2)^2}{4}+\frac{(y-1)^2}{3}=1$

Entonces, x ₁ = 2, y ₁ = -1

y a = 2 y b = √3

Centro = (2, 1)

Eje mayor = 2a = 2(2) = 4

Eje menor = 2b = 2(√3) = 2√3

mi = $\sqrt{1-\frac{b^2}{a^2}}$

mi = 1/2

Focos = (2 ± 1, 1)

(v) 4x ² + 16y ² – 24x – 32y – 12 = 0

Solución:

Dado que 4x ² + 16y ² – 24x – 32y – 12 = 0

4(x ² – 6x) + 16(y ² – 2y) = 12

⁴ (x2 – 6x + 9) + 16( ^y2 – 2y + 1) = 12 + 36 + 16

4(x-3) + 16(y-1) = 64

⇒ $\frac{(x-3)^2}{16}+\frac{(y-1)^2}{4}=1$

Entonces, x ₁ = 3, y ₁ = 1

y a = 4 y b = 2

Centro = (3, 1)

Eje mayor = 2a = 2(4) = 8

Eje menor = 2b = 2(2) = 4

mi = $\sqrt{1-\frac{b^2}{a^2}}$

e = √3/2

Focos = (3 ±2√3; 1)

(vi) x2 ⁺ 4y2 – ^2x = 0

Solución:

Dado que x ² + 4y ² – 2x = 0

(x2 – ^2x ) + 4y2 = ⁰

(x ² – 2x + 1) + 4y ² = 0

(x – 1) ² + 4y ² = 0

⇒ $\frac{(x-1)^2}{1}+\frac{(y)^2}{\frac{1}{4}}=9$

Entonces, x ₁ = 1, y ₁ = 0

y a = 1 y b = 1/4

Centro = (1, 0)

Eje mayor = 2a = 2(1) = 2

Eje menor = 2b = 2(1/2) = 1

mi = $\sqrt{1-\frac{b^2}{a^2}}$

e = √3/2

Focos = (1 ±√3/2, 0)

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra la ecuación de la elipse cuyo foco es (1,–2) y la directriz es 3x – 2y + 5 = 0, y la excentricidad es 1/2.

Pregunta 2. Encuentra la ecuación de la elipse si:

(i) El foco es (0, 1), la directriz es x + y = 0 y e = 1/2.

(ii) El foco es (–1,1), la directriz es x – y + 3 = 0 ye = 1/2.

(iii) El foco es (–2,3), la directriz es 2x + 3y + 4 = 0 y e = 4/5.

(iv) El foco es (1, 2), la directriz es 3x + 4y – 5 = 0 y e = 1/2.

Pregunta 3. Encuentra la excentricidad, las coordenadas de los focos, la longitud del latus-rectum de la elipse:

(yo) 4x 2 + 9y 2 = 1

(ii) 5x 2 + 4y 2 = 1

(iii) 4x 2 + 3y 2 = 1

(iv) 25x 2 + 16y 2 = 1600

(v) 9x 2 + 25y 2 = 225

Pregunta 4. Encuentra la ecuación de la elipse que pasa por el punto (–3, 1) y tiene excentricidad .

Pregunta 5. Encuentra la ecuación de la elipse si:

(i) e = 1/2 y focos (±2, 0).

(ii) e = 2/3 y longitud de latus-rectum = 5

(iii) e = 1/2 y semieje mayor = 4

(iv) e = 1/2 y eje mayor = 12

(v) Pasa por (1, 4) y (–6, 1).

(vi) Sus vértices son (±5, 0) y focos (±4, 0)

(vii) Los vértices son (0, ±13) y los focos (0, ±5)

(viii) Sus vértices son (±6, 0) y focos (±4, 0)

(ix) Extremos del eje mayor (±3, 0) y extremos del eje menor (0, ±2).

(x) Extremos del eje mayor (0, ±√5) y extremos del eje menor (±1, 0).

(xi) La longitud del eje mayor es 26 y los focos (±5, 0).

(xii) La longitud del eje menor es 16 y los focos (0, ±6)

(xiii) Los focos son (±3, 0) y a = 4

Pregunta 6. Encuentra la ecuación de la elipse cuyos focos son (±4, 0), e = 1/3.

Pregunta 7. Encuentra la ecuación de la elipse en la forma estándar cuyo eje menor es igual a la distancia entre los focos y cuyo latus rectum es 10.

Pregunta 8. Encuentra la ecuación de la elipse cuyo centro es (-2, 3) y cuyos semiejes son 3 y 2 cuando el eje mayor es (i) paralelo al eje x (ii) paralelo al eje y .

Pregunta 9. Encuentra la excentricidad de una elipse cuya:

(i) Latus rectum es la mitad de su eje menor

(ii) Latus rectum es la mitad de su eje mayor

Pregunta 10. Encuentra el centro, las longitudes de los ejes, la excentricidad, los focos de la siguiente elipse:

(i) x 2 + 2y 2 – 2x + 12y + 10 = 0

(ii) x 2 + 4y 2 – 4x + 24y + 31 = 0

(iii) 4x 2 + y 2 – 8x + 2y +1 = 0

(iv) 3x 2 + 4y 2 – 12x – 8y + 4 = 0

(v) 4x 2 + 16y 2 – 24x – 32y – 12 = 0

(vi) x2 + 4y2 – 2x = 0

Deja una respuesta Cancelar la respuesta

(yo) 4x ² + 9y ² = 1

(ii) 5x ² + 4y ² = 1

(iii) 4x ² + 3y ² = 1

(iv) 25x ² + 16y ² = 1600

(v) 9x ² + 25y ² = 225

Pregunta 4. Encuentra la ecuación de la elipse que pasa por el punto (–3, 1) y tiene excentricidad $\sqrt{\frac{2}{5}}$ .

(i) x ² + 2y ² – 2x + 12y + 10 = 0

(ii) x ² + 4y ² – 4x + 24y + 31 = 0

(iii) 4x ² + y ² – 8x + 2y +1 = 0

(iv) 3x ² + 4y ² – 12x – 8y + 4 = 0

(v) 4x ² + 16y ² – 24x – 32y – 12 = 0

(vi) x2 ⁺ 4y2 – ^2x = 0