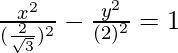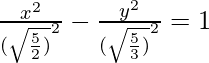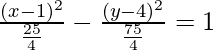Clase 11 RD Sharma Solutions – Capítulo 27 Hipérbola – Ejercicio 27.1

Pregunta 1. La ecuación de la directriz de una hipérbola es x – y + 3 = 0. Su foco es (-1, 1) y excentricidad 3. Encuentra la ecuación de la hipérbola.

Solución:

Dado: Foco = (-1, 1) y Excentricidad = 3

La ecuación de la directriz de una hipérbola ⇒ x – y + 3 = 0.

Sea ‘M’ el punto sobre la directriz y P(x, y) cualquier punto de la hipérbola.

Sabemos, e = PF/PM ⇒ PF ² = e ² PM ²

$⇒ (x+1)^2 + (y-1)^2 = 3^2[\frac{x-y+3}{\sqrt{1^2+(-1)^2}}]$

⇒ 2{x ² + 1 + 2x + y ² + 1 – 2y} = 9{x ² + y ² + 9 + 6x – 6y – 2xy}

⇒ 2x ² + 2 + 4x + 2y ² + 2 – 4y = 9x ² + 9y ² + 81 + 54x – 54y – 18xy

⇒ 2x ² + 4 + 4x + 2y ² – 4y – 9x ² – 9y ² – 81 – 54x + 54y + 18xy = 0

⇒ – 7x ² – 7y ² – 50x + 50y + 18xy – 77 = 0

⇒ 7(x2 + ^{y2 ) –}^18xy + 50x – 50y + 77 = 0

∴La ecuación de la hipérbola es 7(x ² + y ² ) – 18xy + 50x – 50y + 77 = 0.

Pregunta 2. Encuentra la ecuación de la hipérbola cuya

(i) el foco es (0, 3), la directriz es x + y – 1 = 0 y la excentricidad = 2

Solución:

Dado: Foco = (0, 3), Directriz => x + y – 1 = 0 y Excentricidad = 2

Sea ‘M’ el punto sobre la directriz y P(x, y) cualquier punto de la hipérbola.

Sabemos, e = PF/PM ⇒ PF ² = e ² PM ²

$⇒ (x-0)^2 + (y-3)^2 = 2^2[\frac{x+y-1}{\sqrt{1^2+(1)^2}}]^2$

⇒ 2{x ² + y ² + 9 – 6y} = 4{x ² + y ² + 1 – 2x – 2y + 2xy}

⇒ 2x ² + 2y ² + 18 – 12y – 4x ² – 4y ² – 4 – 8x + 8y – 8xy = 0

⇒ – 2x ² – 2y ² – 8x – 4y – 8xy + 14 = 0

⇒ –2(x2 + ^{y2 – 4x +}^2y + 4xy – 7) = 0

⇒ x2 + ^{y2 – 4x +}^2y + 4xy – 7 = 0

∴La ecuación de la hipérbola es x ² + y ² – 4x + 2y + 4xy – 7 = 0.

(ii) el foco es (1, 1), la directriz es 3x + 4y + 8 = 0 y la excentricidad = 2

Solución:

Foco = (1, 1), Directriz => 3x + 4y + 8 = 0 y Excentricidad = 2

Sea ‘M’ el punto sobre la directriz y P(x, y) cualquier punto de la hipérbola.

Sabemos, e = PF/PM ⇒ PF ² = e ² PM ²

$⇒ (x-1)^2 + (y-1)^2 = 2^2[\frac{3x+4y+8}{\sqrt{3^2+(4)^2}}]^2$

⇒ 25{x ² + 1 – 2x + y ² + 1 – 2y} = 4{9x ² + 16y ² + 64 + 24xy + 64y + 48x}

⇒ 25x ² + 25 – 50x + 25y ² + 25 – 50y = 36x ² + 64y ² + 256 + 96xy + 256y + 192x

⇒ 25x ² + 25 – 50x + 25y ² + 25 – 50y – 36x ² – 64y ² – 256 – 96xy – 256y – 192x = 0

⇒ – 11x ² – 39y ² – 242x – 306y – 96xy – 206 = 0

⇒ 11x ² + 96xy + 39y ² + 242x + 306y + 206 = 0

∴La ecuación de la hipérbola es 11x ² + 96xy + 39y ² + 242x + 306y + 206 = 0.

(iii) el foco es (1, 1) la directriz es 2x + y = 1 y la excentricidad = 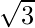$\sqrt{3}$

Solución:

Dado: Foco = (1, 1), Directriz => 2x + y = 1 y Excentricidad = $\sqrt{3}$

Sea ‘M’ el punto sobre la directriz y P(x, y) cualquier punto de la hipérbola.

Sabemos, e = PF/PM ⇒ PF ² = e ² PM ²

$⇒ (x-1)^2 + (y-1)^2 = (\sqrt{3})^2[\frac{2x+y-1}{\sqrt{2^2+(1)^2}}]^2$

⇒ 5{x ² + 1 – 2x + y ² + 1 – 2y} = 3{4x ² + y ² + 1 + 4xy – 2y – 4x}

⇒ 5x ² + 5 – 10x + 5y ² + 5 – 10y = 12x ² + 3y ² + 3 + 12xy – 6y – 12x

⇒ 5x ² + 5 – 10x + 5y ² + 5 – 10y – 12x ² – 3y ² – 3 – 12xy + 6y + 12x = 0

⇒ – 7x ² + 2y ² + 2x – 4y – 12xy + 7 = 0

⇒ 7x ² + 12xy – 2y ² – 2x + 4y– 7 = 0

∴La ecuación de la hipérbola es 7x ² + 12xy – 2y ² – 2x + 4y– 7 = 0.

(iv) el foco es (2, -1), la directriz es 2x + 3y = 1 y la excentricidad = 2

Solución:

Dado: Foco = (2, -1), Directriz => 2x + 3y = 1 y Excentricidad = 2

Sea ‘M’ el punto sobre la directriz y P(x, y) cualquier punto de la hipérbola.

Usando la fórmula, e = PF/PM ⇒ PF ² = e ² PM ²

$⇒ (x-2)^2 + (y+1)^2 = 2^2[\frac{2x+3y-1}{\sqrt{2^2+(3)^2}}]^2$

⇒ 13{x ² + 4 – 4x + y ² + 1 + 2y} = 4{4x ² + 9y ² + 1 + 12xy – 6y – 4x}

⇒ 13x ² + 52 – 52x + 13y ² + 13 + 26y = 16x ² + 36y ² + 4 + 48xy – 24y – 16x

⇒ 13x ² + 52 – 52x + 13y ² + 13 + 26y – 16x ² – 36y ² – 4 – 48xy + 24y + 16x = 0

⇒ – 3x ² – 23y ² – 36x + 50y – 48xy + 61 = 0

⇒ 3x ² + 23y ² + 48xy + 36x – 50y– 61 = 0

∴La ecuación de la hipérbola es 3x ² + 23y ² + 48xy + 36x – 50y– 61 = 0.

(v) el foco es (a, 0), la directriz es 2x + 3y = 1 y la excentricidad = 2

Solución:

Dado: Foco = (a, 0), Directriz => 2x + 3y = 1 y Excentricidad = 2

Sea ‘M’ el punto sobre la directriz y P(x, y) cualquier punto de la hipérbola.

Usando la fórmula, e = PF/PM ⇒ PF ² = e ² PM ²

$⇒ (x-a)^2 + (y-0)^2 = (4/3)^2[\frac{2x-y+a}{\sqrt{2^2+(-1)^2}}]^2$

⇒ 45{x ² + a ² – 2ax + y2} = 16{4x ² + y ² + a ² – 4xy – 2ay + 4ax}

⇒ 45x ² + 45a ² – 90ax + 45y ² = 64x ² + 16y ² + 16a ² – 64xy – 32ay + 64ax

⇒ 45x ² + 45a ² – 90ax + 45y ² – 64x ² – 16y ² – 16a ² + 64xy + 32ay – 64ax = 0

⇒ 19x ² – 29y ² + 154ax – 32ay – 64xy – 29a2 = 0

∴La ecuación de la hipérbola es 19x ² – 29y ² + 154ax – 32ay – 64xy – 29a ² = 0.

(vi) el foco es (2, 2), la directriz es x + y = 9 y la excentricidad = 2

Solución:

Dado: Foco = (2, 2), Directriz => x + y = 9 y Excentricidad = 2

Sea ‘M’ el punto sobre la directriz y P(x, y) cualquier punto de la hipérbola.

Usando la fórmula, e = PF/PM ⇒ PF ² = e ² PM ²

$⇒ (x-2)^2 + (y-2)^2 = (2)^2[\frac{x+y-9}{\sqrt{1^2+(1)^2}}]^2$

⇒ x2 + ⁴ – 4x + ^y2 + 4 – 4y = 2{x2 ⁺ y2 ⁺ 81 + 2xy – 18y – 18x}

⇒ x ² – 4x + y ² + 8 – 4y = 2x ² + 2y ² + 162 + 4xy – 36y – 36x

⇒ x ² – 4x + y ² + 8 – 4y – 2x ² – 2y ² – 162 – 4xy + 36y + 36x = 0

⇒ – x ² – y ² + 32x + 32y + 4xy – 154 = 0

⇒ x2 + ^4xy + y2 ^– 32x – 32y + 154 = 0

∴La ecuación de la hipérbola es x ² + 4xy + y ² – 32x – 32y + 154 = 0.

Pregunta 3. Encuentra la excentricidad, las coordenadas de los focos, las ecuaciones de las directrices y la longitud del lado recto de la hipérbola.

(yo) 9x ² – 16y ² = 144

Solución:

Dado: 9x ² – 16y ² = 144

$⇒ \frac{9x^2}{144}-\frac{16y^2}{144} = 1$

$⇒ \frac{x^2}{16}-\frac{y^2}{9} = 1$

Esto es de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$ donde, a ² = 16, b ² = 9, es decir, a = 4 y b = 3

La excentricidad viene dada por:

$e = \sqrt{1+\frac{b^2}{a^2}}$

$= \sqrt{1+\frac{9}{16}}$

$= \sqrt{\frac{25}{16}}$

Excentricidad $= \frac{5}{4}$

Focos: Las coordenadas de los focos son (±ae, 0)

Focos = (±5, 0)

La ecuación de directrices está dada por: $x = &pm;\frac{a}{e}$ ⇒ 5x ∓ 16 = 0

La longitud de latus-rectum se da como: 2b ² /a = 2(9)/4

Longitud del latus recto = 9/2

(ii) 16x ² – 9y ² = –144

Solución:

Dado: 16x ² – 9y ² = –144

$⇒ \frac{16x^2}{144}-\frac{9y^2}{144} = -1$

$⇒ \frac{x^2}{9}-\frac{y^2}{16} = -1$

Esto es de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2} = -1$ donde, a ² = 9, b ² = 16, es decir, a = 3 y b = 4.

La excentricidad viene dada por:

$e = \sqrt{1+\frac{a^2}{b^2}}$

$= \sqrt{1+\frac{9}{16}}$

$= \sqrt{\frac{25}{16}}$

Excentricidad = $\frac{5}{4}$

Focos: Las coordenadas de los focos son (0, ±be)

(0, ±be) = (0, ±4(5/4))

= (0, ±5).

La ecuación de directrices se da como: x = $&pm;\frac{b}{e}$ ⇒ 5x ∓ 16 = 0.

La longitud de latus-rectum se da como: 2a ² /b = 2(9)/4 = 9/2.

(iii) 4x ² – 3y ² = 36

Solución:

Dado: 4x ² – 3y ² = 36

$⇒ \frac{4x^2}{36}-\frac{3y^2}{36} = 1$

$⇒ \frac{x^2}{9}-\frac{y^2}{12} = 1$

Esto es de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$ donde, a ² = 9, b ² = 12 es decir, a = 3 y b = √12

La excentricidad viene dada por:

$e = \sqrt{1+\frac{b^2}{a^2}}$

$= \sqrt{1+\frac{12}{9}}$

Excentricidad = $\frac{7}{3}.$

Focos : Las coordenadas de los focos son (±ae, 0)= (±ae, 0) = (±√21, 0)

La longitud de latus-rectum se da como = 2b ² /a = 2(12)/3 = 24/3 = 8

(iv) 3x ² – y ² = 4

Solución:

Dado: 3x ² – y ² = 4

$⇒ \frac{3x^2}{4}-\frac{y^2}{4} = 1$

$⇒ \frac{x^2}{\frac{4}{3}}-\frac{y^2}{4} = 1$

$⇒ \frac{x^2}{(\frac{2}{\sqrt3})^2}-\frac{y^2}{(2)^2} = 1$

Esto es de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$ donde, $a = \frac{2}{\sqrt3}$ y b = 2

La excentricidad viene dada por:

$e = \sqrt{1+\frac{b^2}{a^2}}$

$= \sqrt{1+\frac{4}{3}}$

Excentricidad = 2

Focos: Las coordenadas de los focos son (±ae, 0)= (±ae, 0) = ±(2/√3)(2) = ±4/√3

(±ae, 0) = (±4/√3, 0)

La longitud de latus-rectum se da como:= 2b2/a = 2(4)/[2/√3] = 4√3.

(v) 2x ² – 3y ² = 5

Solución:

Dado: 2x ² – 3y ² = 5

$⇒ \frac{2x^2}{5}-\frac{3y^2}{5} = 1$

$⇒ \frac{x^2}{\frac{5}{2}}-\frac{y^2}{\frac{5}{3}} = 1$

$⇒ \frac{x^2}{(\sqrt{\frac{5}{2})}^2}-\frac{y^2}{(\sqrt{\frac{5}{3})}^2} = 1$

Esto es de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ donde, $a = \sqrt{\frac{5}{2}}$ y $b = \sqrt{\frac{5}{3}}$

La excentricidad viene dada por:

$e = \sqrt{1+\frac{b^2}{a^2}}$

$= \sqrt{1+\frac{2}{3}}$

Excentricidad = $\sqrt{\frac{5}{3}}$ .

Focos: Las coordenadas de los focos son (±ae, 0)

o, (±ae, 0) = $(&pm;\frac{5}{\sqrt6}, 0)$

La longitud del latus-rectum se da como: 2b ² /a = $\frac{10\sqrt2}{3\sqrt5}$

Pregunta 4. Encuentra los ejes, la excentricidad, el latus-rectum y las coordenadas de los focos de la hipérbola 25x ² – 36y ² = 225.

Solución:

Dado: 25x ² – 36y ² = 225

$⇒ \frac{25x^2}{225}-\frac{36y^2}{225} = 1$

$⇒ \frac{x^2}{9}-\frac{4y^2}{25} = 1$

$⇒ \frac{x^2}{3^2}-\frac{y^2}{(\frac{5}{2})^2} = 1$

Esto es de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ donde, a = 3 y b = 5/2

La excentricidad viene dada por:

$e = \sqrt{1+\frac{b^2}{a^2}}$

$= \sqrt{1+\frac{25}{36}}$

$= \frac{\sqrt61}{6}$

Focos: Las coordenadas de los focos son (±ae, 0)

(±ae, 0) = (± √61/2, 0)

La longitud de latus-rectum se da como: 2b ² /a

∴ Eje transversal = 6, eje conjugado = 5, e = √61/6, LR = 25/6, focos = (± √61/2, 0)

Pregunta 5. Encuentra el centro , la excentricidad , los focos y las direcciones de la hipérbola

(i) 16x ² – 9y ² + 32x + 36y – 164 = 0

Solución:

Dado: 16x ² – 9y ² + 32x + 36y – 164 = 0.

⇒ 16x ² + 32x + 16 – 9y ² + 36y – 36 – 16 + 36 – 164 = 0

⇒ 16(x ² + 2x + 1) – 9(y ² – 4y + 4) – 16 + 36 – 164 = 0

⇒ 16(x2 + ^2x + 1) – 9( ^y2 – 4y + 4) – 144 = 0

⇒ 16(x + 1) ² – 9(y – 2) ² = 144

Aquí, el centro de la hipérbola es (-1, 2).

Entonces, sea x + 1 = X y y – 2 = Y

La ecuación obtenida es de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ donde, a = 3 y b = 4.

La excentricidad viene dada por:

$e = \sqrt{1+\frac{b^2}{a^2}}$

$= \sqrt{1+\frac{16}{9}}$

$= \frac{5}{3}$

Focos: Las coordenadas de los focos son (±ae, 0)

X = ±5 y Y = 0

x + 1 = ±5 y y – 2 = 0

x = ±5 – 1 y y = 2

x = 4, -6 y y = 2

Entonces, Focos: (4, 2) (-6, 2)

∴ El centro es (-1, 2), excentricidad (e) = 5/3, Focos = (4, 2) (-6, 2), Ecuación de directriz = 5x – 4 = 0 y 5x + 14 = 0.

(ii) x ² – y ² + 4x = 0

Solución:

Dado: x ² – y ² + 4x = 0.

⇒ x2 – y2 ⁺^4x = 0

⇒ x2 ⁺ 4x + 4 – y2 ^– 4 = 0

⇒ (x + 2) ² – y ² = 4

Aquí, el centro de la hipérbola es (2, 0).

La ecuación obtenida es de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ donde, a = 2 y b = 2

La excentricidad viene dada por:

$e = \sqrt{1+\frac{b^2}{a^2}}$

$= \sqrt{1+\frac{4}{4}}$

$= \sqrt{2}$

Focos: Las coordenadas de los focos son (±ae, 0)

X = ± 2√2 y Y = 0

X + 2 = ± 2√2 y Y = 0

X= ± 2√2 – 2 y Y = 0

Entonces, Focos = (± 2√2 – 2, 0)

∴ El centro es (-2, 0), excentricidad (e) = √2, Focos = (-2± 2√2, 0), Ecuación de directriz = x + 2 = ±√2.

(iii) x ² – 3y ² – 2x = 8

Solución:

Dado: x ² – 3y ² – 2x = 8.

⇒ x ² – 3y ² – 2x = 8

⇒ x ² – 2x + 1 – 3y ² – 1 = 8

⇒ (x – 1) ² – 3y ² = 9

Aquí, el centro de la hipérbola es (1, 0)

La ecuación obtenida es de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ donde, a = 3 y b = √3

La excentricidad viene dada por:

$e = \sqrt{1+\frac{b^2}{a^2}}$

$= \sqrt{1+\frac{3}{9}}$

$= \frac{2\sqrt{3}}{3}$

Focos: Las coordenadas de los focos son (±ae, 0)

X = ± 2√3 y Y = 0

X – 1 = ± 2√3 y Y = 0

X= ± 2√3 + 1 y Y = 0

Entonces, Focos = (1 ± 2√3, 0)

∴ El centro es (1, 0), excentricidad (e) = 2√3/3, Focos = (1 ± 2√3, 0), Ecuación de directriz = X = 1±9/2√3.

Pregunta 6. Hallar la ecuación de la hipérbola, referida a sus ejes principales como ejes de coordenadas, en los siguientes casos:

(i) la distancia entre los focos = 16 y la excentricidad = √2

Solución:

Dado: Distancia entre los focos = 16 y Excentricidad = √2

Comparemos con la ecuación de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ …..(1)

La distancia entre los focos es 2ae y b ² = a ² (e ² – 1)

Entonces, 2ae = 16

⇒ ae = 16/2

⇒ a√2 = 8

⇒ a = 8/√2

⇒ un ² = 64/2 = 32

Sabemos que, b ² = a ² (e ² – 1)

Entonces, b2 ⁼ 32[(√2)2 – 1]

= 32(2 – 1)

= 32

La ecuación de la hipérbola se da como $\frac{x^2}{32}-\frac{y^2}{32}=1$

⇒ x2 – ^y2⁼ 32

∴ La ecuación de la hipérbola es x ² – y ² = 32.

(ii) el eje conjugado es 5 y la distancia entre focos = 13

Solución:

Dado: Eje conjugado = 5 y Distancia entre focos = 13

Comparemos con la ecuación de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ …..(1)

La distancia entre los focos es 2ae y b ² = a ² (e ² – 1)

La longitud del eje conjugado es 2b

Entonces, 2b = 5

⇒ segundo = 5/2

⇒ ^{segundo 2} = 25/4

Sabemos que, 2ae = 13

ae = 13/2

⇒ un ^{2 mi}² = 169/4

segundo ² = un ² (e ² – 1)

⇒ ^{segundo 2} = un ² mi ² – un ²

⇒ 25/4 = 169/4 – un ²

⇒ un ² = 169/4 – 25/4

⇒ un ² = 144/4 = 36

La ecuación de la hipérbola se da como $\frac{x^2}{36}-\frac{y^2}{\frac{25}{4}}=1$

$⇒ \frac{x^2}{36}-\frac{4y^2}{25}=1$

∴ La ecuación de la hipérbola es 25x ² – 144y ² = 900.

(iii) el eje conjugado es 7 y pasa por el punto (3, -2)

Solución:

Dado: Eje conjugado = 7 y Pasa por el punto (3, -2)

El eje conjugado es 2b

Entonces, 2b = 7

⇒ b = 7/2

⇒ ^{segundo 2} = 49/4

La ecuación de la hipérbola se da como $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

Como pasa por los puntos (3, -2), tenemos

$\frac{3^2}{a^2}-\frac{(-2)^2}{b^2}=1$

$⇒ \frac{9}{a^2}-\frac{4}{\frac{49}{4}}=1$

⇒ un ² = 441/65

La ecuación de la hipérbola se da como: $\frac{x^2}{\frac{441}{65}}-\frac{y^2}{\frac{49}{4}}=1$

∴ La ecuación de la hipérbola es 65x ² – 36y ² = 441.

Pregunta 7. Encuentra la ecuación de la hipérbola cuya:

(i) los focos son (6,4) y (-4,4) y la excentricidad es 2.

Solución:

Claramente, las coordenadas del centro son (1,4).

La ecuación de la hipérbola es:

$\frac{(x-1)^2}{a^2}-\frac{(y-4)^2}{b^2} = 1$

Distancia entre los focos = 2ae

⇒ 2ae = 10

⇒ un = 5/2

⇒ un ² = 25/4

Ya que, b ² = a ² (e ² – 1)

⇒ ^{segundo 2} = 75/4

Poniendo los valores en la ecuación, obtenemos

$\frac{(x-1)^2}{\frac{25}{4}}-\frac{(y-4)^2}{\frac{75}{4}} = 1$

⇒ 12×2 – 4y2 – 24x + 32y -127 = 0.

(ii) los vértices son (-8,-1) y (16,-1) y el foco es (17,-1)

Solución:

Claramente, las coordenadas del centro son (4,-1).

La ecuación de la hipérbola es:

$\frac{(x-4)^2}{a^2}-\frac{(y+1)^2}{b^2} = 1$

Distancia entre vértices = 2ae

⇒ 24 = 2a

⇒ un = 12

⇒ a ² = 144 y e ² = 169/144

Ya que, b ² = a ² (e ² – 1)

⇒ ^{segundo 2} = 25

Poniendo los valores en la ecuación, obtenemos

$\frac{(x-1)^2}{144}-\frac{(y-4)^2}{25} = 1$

⇒ 25x ² – 144y ² – 200x – 288y – 3344 = 0.

(iii) los focos son (4, 2) y (8, 2) y la excentricidad es 2.

Solución:

Claramente, las coordenadas del centro son (6, 2).

La ecuación de la hipérbola es:

$\frac{(x-6)^2}{a^2}-\frac{(y-2)^2}{b^2} = 1$

Distancia entre los focos = 2ae

⇒ 2ae = 4

⇒ un = 1

Ya que, b ² = a ² (e ² – 1)

⇒ ^{segundo 2} =3

Poniendo los valores en la ecuación, obtenemos

$\frac{(x-6)^2}{1}-\frac{(y-2)^2}{3} = 1$

⇒ 3×2 – y2 – 36x + 4y + 101 = 0.

(iv) los vértices son (0, ±7) y los focos en (0, ±28/3).

Solución:

Los vértices de las coordenadas son (0, ±b) y (0, ±be).

⇒ segundo = 7

⇒ ^{segundo 2} = 49

y, ser = 28/3

⇒ mi = 4/3 ⇒ mi ² = 16/9

Ahora, a ² = b ² (e ² -1)

⇒ un ² = 343/9

La ecuación se convierte en:

$\frac{x^2}{\frac{343}{9}}-\frac{y^2}{49} = 1$

(v) los vértices están en (±6, 0) y una de las directrices es x = 4.

Solución:

Se da que los vértices de la hipérbola son (±6, 0).

=> un = 6

=> un ² = 36

Ahora, x = 4

=> a/e = 4

=> 6/e = 4

=> mi = 3/2

Ahora sabemos,

(ae) ² = un ² + ^{segundo 2}

(6 × (3/2)) ² = 6 ² + ^{segundo 2}

b ² = 81 – 36

b ² = 45

La ecuación se convierte en,

$\frac{x^2}{36} - \frac{y^2}{45} = 1$

(vi) Cuyos focos están en (± 2, 0) y la excentricidad es 3/2.

Solución:

Tenemos los focos dados como, (± 2, 0).

Aquí e = 3/2. Sabemos,

ae = 2

=> un = 2/e

=> un = 2/(3/2)

=> un = 4/3

Ahora sabemos,

(ae) ² = un ² + ^{segundo 2}

(2) ² = (4/3) ² + ^{segundo 2}

b ² = 4 – 16/3

b2 ⁼ 20/9

Entonces la ecuación se convierte en,

=> $\frac{9 x^2}{16} - \frac{9 y^2}{20} = 1$

=> $\frac{x^2}{4} - \frac{y^2}{5} = \frac{4}{9}$

Pregunta 8. Encuentra la excentricidad si la longitud del eje conjugado es 3/4 de la longitud del eje transversal .

Solución:

Dado: 2b = 6a/4

⇒ b/a = 3/4

⇒ b ² /a ² = 9/16

Ahora, $e = \sqrt{1+\frac{b^2}{a^2}}$

$= \sqrt{\frac{25}{16}}$

mi = 5/4.

Pregunta 9. Encuentra la ecuación de la hipérbola cuyo foco está en (5,2) y (4,2) y centro en (3,2).

Solución:

Claramente las coordenadas del primer vértice son (2,2).

La ecuación de la hipérbola es:

$\frac{(x-3)^2}{a^2}-\frac{(y-2)^2}{b^2} = 1$

Distancia entre 2 vértices = 2a

⇒ un = 1

y, e = 2

segundo ² = un ² (e ² – 1)

⇒ ^{segundo 2} = 3

La ecuación se convierte en:

$\frac{(x-3)^2}{1}-\frac{(y-2)^2}{3} = 1$

⇒ 3(x-3) ² – (y-2) ² = 3.

Pregunta 10. Si P es cualquier punto de la hipérbola cuyo eje es igual, demuestre que SP.S’P = CP ² .

Solución:

Dado: a = b

La ecuación se convierte en: x ² – y ² = a ²

$e = \sqrt{2}$ , C = (0,0), $S = (\sqrt{2}a,0)$ y $S' = (-\sqrt{2}a,0)$

SP. S’P = 4a ⁴ + 4a ² (a ² + b ² ) + (a ² + b ² ) ² – 8a ² b ²

= (a ² + b ² ) ² = PC

Por lo tanto, SP.S’P = CP ² .

Pregunta 11. Encuentra la ecuación de la hipérbola cuya:

(i) los focos son (±2,0) y los focos son (±3,0).

Solución:

La ecuación de la hipérbola es:

$\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$

Distancia entre los focos = 2ae

⇒ un = 2

⇒ un ² = 4

mi = 3/2

Ya que, b ² = a ² (e ² – 1)

⇒ ^{segundo 2} = 5

Poniendo los valores en la ecuación, obtenemos

$\frac{x^2}{4}-\frac{y^2}{5} = 1.$

(ii) los vértices son (0, ±4) y los focos en (0, ±2/3).

Solución:

Los vértices de las coordenadas son (0, ±b) y (0, ±be).

⇒ segundo = 4

⇒ ^{segundo 2} = 16

y, ser = 2/3

⇒ mi = 2/3 ⇒ mi ² = 4/9

Ahora, a ² = b ² (e ² -1)

⇒ un ² = 343/9

La ecuación se convierte en:

$\frac{x^2}{\frac{343}{9}}-\frac{y^2}{49} = 1$

Pregunta 12. Encuentra la ecuación cuando la distancia entre focos es 16 y la excentricidad es 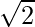$\sqrt{2}$ .

Solución:

Distancia entre focos = 2ae = 16

$⇒ 2a(\sqrt{2}) = 16$

$⇒ a = \frac{16}{2\sqrt{2}}$

$⇒ a = 4\sqrt{2}$

$e = \frac{\sqrt{a^2+b^2}}{a}$

o, b ² = 32

La ecuación se convierte en: x ² – y ² = 32.

Pregunta 13. Muestre que el conjunto de todos los puntos tales que la diferencia de sus distancias desde (4,0) y (-4,0) es siempre igual a 2 representa una hipérbola.

Solución:

Sea P(x, y) el punto del conjunto.

Distancia de P desde (4,0) = $\sqrt{(x-4)^2+y^2}$

Distancia de P a (-4,0) = $\sqrt{(x+4)^2+y^2}$

Dado:

$\sqrt{(x-4)^2+y^2} - \sqrt{(x+4)^2+y^2} = 2$

$⇒ \sqrt{(x-4)^2+y^2} = \sqrt{(x+4)^2+y^2} + 2$

Elevando al cuadrado ambos lados, tenemos

$-4x-1 = \sqrt{(x+4)^2+y^2}$

⇒ 15x ² – y ² = 15.

Por lo tanto, P representa una hipérbola.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. La ecuación de la directriz de una hipérbola es x – y + 3 = 0. Su foco es (-1, 1) y excentricidad 3. Encuentra la ecuación de la hipérbola.

Pregunta 2. Encuentra la ecuación de la hipérbola cuya

(i) el foco es (0, 3), la directriz es x + y – 1 = 0 y la excentricidad = 2

(ii) el foco es (1, 1), la directriz es 3x + 4y + 8 = 0 y la excentricidad = 2

(iii) el foco es (1, 1) la directriz es 2x + y = 1 y la excentricidad =

(iv) el foco es (2, -1), la directriz es 2x + 3y = 1 y la excentricidad = 2

(v) el foco es (a, 0), la directriz es 2x + 3y = 1 y la excentricidad = 2

(vi) el foco es (2, 2), la directriz es x + y = 9 y la excentricidad = 2

Pregunta 3. Encuentra la excentricidad, las coordenadas de los focos, las ecuaciones de las directrices y la longitud del lado recto de la hipérbola.

(yo) 9x 2 – 16y 2 = 144

(ii) 16x 2 – 9y 2 = –144

(iii) 4x 2 – 3y 2 = 36

(iv) 3x 2 – y 2 = 4

(v) 2x 2 – 3y 2 = 5

Pregunta 4. Encuentra los ejes, la excentricidad, el latus-rectum y las coordenadas de los focos de la hipérbola 25x 2 – 36y 2 = 225.

Pregunta 5. Encuentra el centro , la excentricidad , los focos y las direcciones de la hipérbola

(i) 16x 2 – 9y 2 + 32x + 36y – 164 = 0

(ii) x 2 – y 2 + 4x = 0

(iii) x 2 – 3y 2 – 2x = 8

Pregunta 6. Hallar la ecuación de la hipérbola, referida a sus ejes principales como ejes de coordenadas, en los siguientes casos:

(i) la distancia entre los focos = 16 y la excentricidad = √2

(ii) el eje conjugado es 5 y la distancia entre focos = 13

(iii) el eje conjugado es 7 y pasa por el punto (3, -2)

Pregunta 7. Encuentra la ecuación de la hipérbola cuya:

(i) los focos son (6,4) y (-4,4) y la excentricidad es 2.

(ii) los vértices son (-8,-1) y (16,-1) y el foco es (17,-1)

(iii) los focos son (4, 2) y (8, 2) y la excentricidad es 2.

(iv) los vértices son (0, ±7) y los focos en (0, ±28/3).

(v) los vértices están en (±6, 0) y una de las directrices es x = 4.

(vi) Cuyos focos están en (± 2, 0) y la excentricidad es 3/2.

Pregunta 8. Encuentra la excentricidad si la longitud del eje conjugado es 3/4 de la longitud del eje transversal .

Pregunta 9. Encuentra la ecuación de la hipérbola cuyo foco está en (5,2) y (4,2) y centro en (3,2).

Pregunta 10. Si P es cualquier punto de la hipérbola cuyo eje es igual, demuestre que SP.S’P = CP 2 .

Pregunta 11. Encuentra la ecuación de la hipérbola cuya:

(i) los focos son (±2,0) y los focos son (±3,0).

(ii) los vértices son (0, ±4) y los focos en (0, ±2/3).

Pregunta 12. Encuentra la ecuación cuando la distancia entre focos es 16 y la excentricidad es .

Pregunta 13. Muestre que el conjunto de todos los puntos tales que la diferencia de sus distancias desde (4,0) y (-4,0) es siempre igual a 2 representa una hipérbola.

Deja una respuesta Cancelar la respuesta

(iii) el foco es (1, 1) la directriz es 2x + y = 1 y la excentricidad = $\sqrt{3}$

(yo) 9x ² – 16y ² = 144

(ii) 16x ² – 9y ² = –144

(iii) 4x ² – 3y ² = 36

(iv) 3x ² – y ² = 4

(v) 2x ² – 3y ² = 5

Pregunta 4. Encuentra los ejes, la excentricidad, el latus-rectum y las coordenadas de los focos de la hipérbola 25x ² – 36y ² = 225.

(i) 16x ² – 9y ² + 32x + 36y – 164 = 0

(ii) x ² – y ² + 4x = 0

(iii) x ² – 3y ² – 2x = 8

Pregunta 10. Si P es cualquier punto de la hipérbola cuyo eje es igual, demuestre que SP.S’P = CP ² .

Pregunta 12. Encuentra la ecuación cuando la distancia entre focos es 16 y la excentricidad es $\sqrt{2}$ .