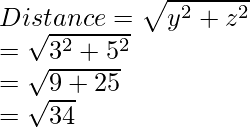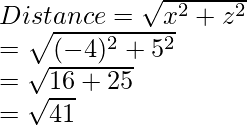Pregunta 1: Nombre los octantes en los que se encuentran los siguientes puntos:
(yo) (5, 2, 3)
(ii) (-5, 4, 3)
(iii) (4, -3, 5)
(iv) (7, 4, -3)
(v) (-5, -4, 7)
(vi) (-5, -3, -2)
(vii) (2, -5, -7)
(viii) (-7, 2, -5)
Solución:
(yo) (5, 2, 3)
Aquí, dado que x, y y z los tres son positivos, entonces el octante será XOYZ
(ii) (-5, 4, 3)
Aquí, dado que x es negativo e y y z son positivos, entonces el octante será X′OYZ
(iii) (4, -3, 5)
En este caso, dado que y es negativo y x y z son positivos, el octante será XOY′Z
(iv) (7, 4, -3)
Aquí, dado que z es negativo y x e y son positivos, entonces el octante será XOYZ′
(v) (-5, -4, 7)
Aquí, dado que x e y son negativos y z es positivo, el octante será X′OY′Z
(vi) (-5, -3, -2)
Aquí, dado que x, y y z los tres son negativos, entonces el octante será X′OY′Z′
(vii) (2, -5, -7)
Aquí, dado que z e y son negativos y x es positivo, el octante será XOY′Z′
(viii) (-7, 2, -5)
Aquí, dado que x y z son negativos y x es positivo, el octante será X′OYZ′
Pregunta 2: Encuentra la imagen de:
(i) (-2, 3, 4) en el plano yz
(ii) (-5, 4, -3) en el plano xz
(iii) (5, 2, -7) en el plano xy
(iv) (-5, 0, 3) en el plano xz
(v) (-4, 0, 0) en el plano xy
Solución:
(yo) (-2, 3, 4)
Podemos cambiar la coordenada x para encontrar la imagen correspondiente en el plano yz.
Por lo tanto, Imagen del punto (-2, 3, 4) es (2, 3, 4)
(ii) (-5, 4, -3)
Podemos cambiar la coordenada y para encontrar la imagen correspondiente en el plano xz.
Aquí, la imagen del punto (-5, 4, -3) es (-5, -4, -3)
(iii) (5, 2, -7)
Podemos cambiar la coordenada z para encontrar la imagen correspondiente en el plano xy.
Aquí, la imagen del punto (5, 2, -7) es (5, 2, 7)
(iv) (-5, 0, 3)
Podemos cambiar la coordenada y para encontrar la imagen correspondiente en el plano xz.
Aquí, la imagen del punto (-5, 0, 3) es (-5, 0, 3)
(v) (-4, 0, 0)
Podemos cambiar la coordenada z para encontrar la imagen correspondiente en el plano xy.
Aquí, la imagen del punto (-4, 0, 0) es (-4, 0, 0)
Pregunta 3: Un cubo de lado 5 tiene un vértice en el punto (1, 0, 1), y las tres aristas de este vértice son, respectivamente, paralelas a los ejes x e y negativos y al eje z positivo. Encuentra las coordenadas de los otros vértices del cubo.
Solución:
Dado:

Un cubo tiene lado 4 con un vértice en (1, 0, 1)
Lado del cubo = 5
Tenemos que encontrar las coordenadas de los otros vértices del cubo.
Asi que,
Deje que el Punto A(1, 0, 1) y AB, AD y AE sean paralelos al eje x -ve, al eje y -ve y al eje z +ve respectivamente.
Como lado del cubo = 5
El punto B es (-4, 0, 1)
El punto D es (1, -5, 1)
El punto E es (1, 0, 6)
Ahora, EH es paralelo a –ve eje y
El punto H es (1, -5, 6)
HG es paralelo al eje x -ve
El punto G es (-4, -5, 6)
Ahora, nuevamente GC y GF son paralelos al eje z -ve y al eje y +ve respectivamente
El punto C es (-4, -5, 1)
El punto F es (-4, 0, 6)
Pregunta 4: Los planos se dibujan paralelos a los planos de coordenadas a través de los puntos (3, 0, -1) y (-2, 5, 4). Encuentre las longitudes de los bordes del paralelepípedo así formado.
Solución:
Dado:
Los puntos son (3, 0, -1) y (-2, 5, 4)
Tenemos que hallar las longitudes de las aristas del paralelepípedo formado.
Para el punto (3, 0, -1)
x 1 = 3, y 1 = 0 y z 1 = -1
Para el punto (-2, 5, 4)
x 2 = -2, y 2 = 5 y z 2 = 4
El plano paralelo a los planos coordenados de x 1 y x 2 es el plano yz
El plano paralelo a los planos de coordenadas de y 1 y y 2 es el plano xz
El plano paralelo a los planos de coordenadas de z 1 y z 2 es el plano xy
Distancia entre planos x 1 = 3 y x 2 = -2 es 3 – (-2) = 3 + 2 = 5
La distancia entre los planos x 1 = 0 y y 2 = 5 es 5 – 0 = 5
La distancia entre los planos z 1 = -1 y z 2 = 4 es 4 – (-1) = 4 + 1 = 5
Por lo tanto,
Las aristas del paralelepípedo son 5, 5, 5
Pregunta 5: Los planos se dibujan a través de los puntos (5, 0, 2) y (3, -2, 5) paralelos a los planos de coordenadas. Encuentre las longitudes de los bordes del paralelepípedo rectangular así formado.
Solución:
Dado:
Los puntos son (5, 0, 2) y (3, -2, 5)
Tenemos que encontrar las longitudes de las aristas del paralelepípedo formado
Para el punto (5, 0, 2)
x 1 = 5, y 1 = 0 y z 1 = 2
Para el punto (3, -2, 5)
x 2 = 3, y 2 = -2 y z 2 = 5
El plano paralelo a los planos coordenados de x 1 y x 2 es el plano yz
El plano paralelo a los planos de coordenadas de y 1 y y 2 es el plano xz
El plano paralelo a los planos de coordenadas de z 1 y z 2 es el plano xy
La distancia entre los planos x 1 = 5 y x 2 = 3 es 5 – 3 = 2
La distancia entre los planos y 1 = 0 y y 2 = -2 es 0 – (-2) = 0 + 2 = 2
La distancia entre los planos z 1 = 2 y z 2 = 5 es 5 – 2 = 3
Por lo tanto,
Las aristas del paralelepípedo son 2, 2, 3
Pregunta 6: Encuentra las distancias del punto P (-4, 3, 5) desde los ejes de coordenadas.
Solución:
Dado:
El punto P (-4, 3, 5)
La distancia del punto desde el eje x se da como:
La distancia del punto desde el eje y se da como:
La distancia del punto desde el eje z se da como:
Pregunta 7: Las coordenadas de un punto son (3, -2, 5). Escriba las coordenadas de siete puntos tales que los valores absolutos de sus coordenadas sean los mismos que los de las coordenadas del punto dado.
Solución:
Dado:
Punto (3, -2, 5)
El valor absoluto de cualquier punto (x, y, z) se muestra mediante,
√( x2 + y2 + z2 )
Necesitamos asegurarnos de que el valor absoluto sea el mismo para todos los puntos.
Así que sea el punto A(3, -2, 5)
Los 7 puntos restantes son:
Punto B(3, 2, 5) (Al cambiar el signo de la coordenada y)
Punto C(-3, -2, 5) (Al cambiar el signo de la coordenada x)
Punto D(3, -2, -5) (Al cambiar el signo de la coordenada z)
Punto E(-3, 2, 5) (Al cambiar el signo de las coordenadas x e y)
Punto F(3, 2, -5) (Al cambiar el signo de las coordenadas y y z)
Punto G(-3, -2, -5) (Al cambiar el signo de las coordenadas x y z)
Punto H(-3, 2, -5) (Al cambiar el signo de las coordenadas x, y y z)