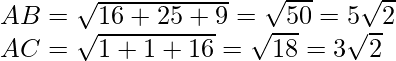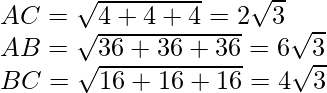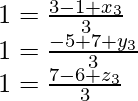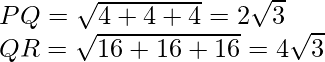Clase 11 Soluciones RD Sharma – Capítulo 28 Introducción a la geometría de coordenadas 3D – Ejercicio 28.3

Pregunta 1. Los vértices del triángulo son A(5, 4, 6), B(1, -1, 3) y C(4, 3, 2). La bisectriz interna del ángulo A se encuentra con BC en D. Encuentra las coordenadas de D y la longitud AD.

Solución:

Sabemos que la bisectriz del ángulo divide al lado opuesto en razón de otros dos lados

⇒D divide a BC en razón de AB:AC

A(5, 4, 6), B(1, -1, 3) y C(4, 3, 2)

$AB=\sqrt{16+25+9}=\sqrt{50}=5\sqrt{2}\\ AC=\sqrt{1+1+16}=\sqrt{18}=3\sqrt{2}$

AB:AC=5:3=m:n

$D(x,y)=(\frac{mx_2+mx_1}{m+n},\frac{my_2+my_1}{m+n},\frac{mz_2+zn_1}{m+n})$

Valores de sustitución para m:n=5:3

(x ₁ ,y ₁ ,z ₁ )=(1,-1,3)

(x ₂ ,y ₂ ,z ₂ )=(4,3,2)

$D=(\frac{22}{8},\frac{3}{2},\frac{19}{8})$

Pregunta 2. Un punto C con coordenada z 8 se encuentra en el segmento de línea que une los puntos A (2, -3, 4) y B (8, 0, 10). Encuentra sus coordenadas.

Solución:

Coordenada Z 8

A(2, -3, 4) y B(8, 0, 10)

DR de AB=(6,3,6)

DR de BC=(x-8,y-0,8-10)

Dado que A,B,C se encuentran en la misma línea

Entonces los valores de DR deben ser proporcionales

$\frac{x-8}{6}=\frac{y}{3}=\frac{8-10}{6}$

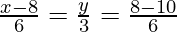
Entonces x=6, y=-1

el punto es (6,-1,8)

Pregunta 3. Demuestra que tres puntos A(2, 3, 4), B(-1, 2, -3) y C(-4, 1, -10) son colineales y encuentra la razón en la que C divide a AB.

Solución:

Si los puntos son colineales, todos los puntos se encuentran en la misma línea

y los DR deben ser proporcionales

A(2, 3, 4), B(-1, 2, -3) y C(-4, 1, -10)

DR de AB=(3,1,7)

DR de BC = (3,1,7)

Entonces A,B,C son colineales

Longitud de CA $=\sqrt{36+4+196}=\sqrt{236}$

Longitud de AB $=\sqrt{9+1+49}=\sqrt{59}$

La relación es AC:AB=2:1

Entonces C divide a AB en razón 2:1 externamente

Pregunta 4. Encuentra la razón en la que la línea que une (2, 4, 5) y (3, 5, 4) se divide por el plano yz.

Solución:

plano yz significa x=0

Dado (2,4,5) y (3,5,4)

Suponga que la relación es m:n

Igualemos x término

$0=\frac{3m+2n}{m+n}$

3m=-2n

m:n=-2:3

Lo que significa que el plano yz divide la línea en una proporción de 2:3 externamente.

Pregunta 5. Halla la razón en que el segmento de recta que une los puntos (2, -1, 3) y (-1, 2, 1) se divide por el plano x+ y + z = 5.

Solución:

(2, -1, 3) y (-1, 2, 1)

x+y+z=5

Supongamos que el plano divide a la línea en razón λ:1

entonces el punto P, que es una línea divisoria en relación λ: 1, es

$P=(\frac{-λ+2}{λ+1},\frac{2λ-1}{λ+1},\frac{λ+3}{λ+1})$

P se encuentra en el plano x+y+z=5

-λ+2+2λ-1+λ+3=5λ5

3λ=-1⇒λ=-1:3

Pregunta 6. Si los puntos A(3, 2, -4), B(9, 8, -10) y C(5, 4, -6) son colineales, encuentra la razón en la que C divide a AB.

Solución:

A(3, 2, -4), B(9, 8, -10) y C(5, 4, -6)

$AC=\sqrt{4+4+4}=2\sqrt{3}\\ AB=\sqrt{36+36+36}=6\sqrt{3}\\ BC=\sqrt{16+16+16}=4\sqrt{3}$

CA: BC = 1: 2

Pregunta 7. Los puntos medios de los lados de un triángulo ABC están dados por (-2, 3, 5), (4, -1, 7) y (6, 5, 3). Encuentre las coordenadas de A, B y C.

Solución:

Dados los puntos medios (-2, 3, 5), (4, -1, 7) y (6, 5, 3)

Suponga que D es el punto medio de AB, E es el punto medio de BC

F es el punto medio de CA

A(x ₁ ,y ₁ ,z ₁ ) B(x ₂ ,y ₂ ,z ₂ ) C(x ₃ ,y ₃ ,z ₃ )

De la fórmula del punto medio, obtenemos las siguientes ecuaciones

x ₁ + x ₂ = -4; x ₂ + x ₃ = 8; x ₃ + x ₁ = 12

y1 + y2 ₌₆ ; y2 ₊ y3 =-2 _;y ₃ + y ₁ = 10

z ₁ + z ₂ = 10; z ₂ + z ₃ = 14; z ₃ + z ₁ = 6

Resolviendo el conjunto de ecuaciones anterior obtenemos

A=(0,9,1)

B=(-4,-3,9)

C=(12,1,5)

Pregunta 8. A(1, 2, 3), B(0, 4, 1), C(-1, -1, -3) son los vértices de un triángulo ABC. Encuentra el punto en el que la bisectriz del ángulo ∠BAC intersecta a BC.

Solución:

A(1, 2, 3), B(0, 4, 1), C(-1, -1, -3)

La bisectriz del ángulo en A divide a BC en razón de AB:AC

$AB=\sqrt{1+4+4}=3 AC=\sqrt{4+9+36}=7$

Supongamos que D divide a BC

asi que $D=(\frac{-3}{10},\frac{25}{10},\frac{-2}{10})$

Pregunta 9. Halla la razón en que la esfera x2+y2 +z2 = 504 divide la recta que une los puntos (12, -4, 8) y (27, -9, 18).

Solución:

(12, -4, 8) y (27, -9, 18)

Supongamos que el punto P es la razón de la línea divisoria λ:1, obtenemos

$P=(\frac{27λ+12}{λ+1},\frac{-9λ-4}{λ+1},\frac{8λ+8}{λ+1})$

P se encuentra en la esfera, así que sustituye en la ecuación de la esfera

x ² + y ² + z ² = 504

9(λ+4) ² +(9λ+4) ² +4(9λ+4) ² =504(λ+1) ²

729λ ² +81λ ² +324λ ² +648λ+72λ+288λ+144+16+64=504λ ² +1008λ+504

(1134-504)λ ² +(1008-1008)λ+224-504=0

630λ2=280

λ2=4/9

λ=2:3

Pregunta 10. Demostrar que el plano ax + by + cz + d = 0 divide la recta que une los puntos (x ₁ ,y ₁ ,z ₁ ) y (x ₂ ,y ₂ ,z ₂ ) en la razón 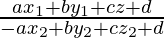$\frac{ax_1+by_1+cz+d}{-ax_2+by_2+cz_2+d}$

Solución:

Suponga que la relación es λ: 1

El plano es ax+by+cz+d=0

puntos (x ₁ ,y ₁ ,z ₁ ) y (x ₂ ,y ₂ ,z ₂ )

Suponga que el punto de intersección de la línea y el plano es D

$D=(\frac{λx_2+x_1}{λ+1},\frac{λy_2+y_1}{λ+1},\frac{λz_2+z_1}{λ+1})$

Como D está en el plano, sustituimos D en la ecuación del plano y obtenemos

λ(ax ₂ +por ₂ +cz ₂ +d)+ax ₁ +por ₁ +cz ₁ +d=0

⇒ $λ=-\frac{ax_1+by_1+cz_1+d}{ax_2+by_2+cz_2+d}$

Pregunta 11. Encuentra el baricentro de un triángulo cuyos puntos medios son (1, 2, -3), (3, 0, 1) y (-1, 1, -4).

Solución:

(1, 2, -3), (3, 0, 1) y (-1, 1, -4)

El centroide del triángulo está dado por

$(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3},\frac{z_1+z_2+z_3}{3})$

Lo sabemos

x ₁ + x ₂ = 2

x ₂ + x ₃ = 6

x ₁ + x ₃ = -2

Sumar todo da ⇒2(x ₁ +x ₂ +x ₃ )=6

entonces x ₁ + x ₂ + x ₃ = 3

De manera similar, y ₁ +y ₂ +y ₃ =3, z ₁ +z ₂ +z ₃ =-6

centroide =(1,1,-2)

Pregunta 12. El baricentro de un triángulo ABC está en el punto (1, 1, 1). Si las coordenadas de A y B son (3, -5, 7) y (-1, 7, -6) respectivamente, encuentre las coordenadas del punto C.

Solución:

Centroide dado (1,1,1)

A(3,-5,7) y B(-1,7,-6)

Igualando términos, obtenemos

$1=\frac{3-1+x_3}{3}\\ 1=\frac{-5+7+y_3}{3}\\ 1=\frac{7-6+z_3}{3}$

(x ₃ ,y ₃ ,z ₃ )=(1,1,2)

Pregunta 13. Encuentra las coordenadas de los puntos que trisecan el segmento de recta que une los puntos P(4, 2, -6) y Q(10, -16, 6).

Solución:

Los puntos de trisección son aquellos que dividen la línea en proporción 1:2 o 2:1

P(4, 2, -6) y Q(10, -16, 6)

Considere el caso 1:2, obtenemos

$(\frac{10+8}{3},\frac{-16+4}{3},\frac{6-12}{3})=(6,-4,-2)$

considerar 2:! caso, obtenemos

$(\frac{20+4}{3},\frac{-32+2}{3},\frac{12-6}{3})=(8,-10,2)$

(6,-4,-2) y (8,-10,2) son puntos de trisección

Pregunta 14. Usando la fórmula de la sección, demuestre que los puntos A(2, -3, 4), B(-1, 2, 1) y C(0, 1/3, 2) son colineales.

Solución:

A(2, -3, 4), B(-1, 2, 1) y C(0, 1/3, 2)

Los DR de BC son $(-1,\frac{5}{3},-1)$

Los DR de AC son $(2,\frac{-10}{3},2)$

Está claro que todos los DR son proporcionales.

Pregunta 15. Dado que P(3, 2, -4), Q(5, 4, -6) y R(9, 8, -10) son colineales. Encuentra la razón en la que Q divide a PR.

Solución:

P(3, 2, -4), Q(5, 4, -6) y R(9, 8, -10)

$PQ=\sqrt{4+4+4}=2\sqrt{3}\\ QR=\sqrt{16+16+16}=4\sqrt{3}$

PQ:QR=1:2

Pregunta 16. Encuentra la razón en la que el segmento de línea que une los puntos (4, 8, 10) y (6, 10, -8) se divide por el plano yz.

Solución:

(4, 8, 10) y (6, 10, -8) se divide por el plano yz

La ecuación del plano yz es x=0

Suponga que la relación es m: n

Igualando el término x, obtenemos

$0=\frac{6m+4n}{m+n}$

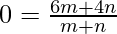
m:n=-2:3

Entonces, el plano XY divide el segmento de línea en una proporción de 2:3 externamente.

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Los vértices del triángulo son A(5, 4, 6), B(1, -1, 3) y C(4, 3, 2). La bisectriz interna del ángulo A se encuentra con BC en D. Encuentra las coordenadas de D y la longitud AD.

Pregunta 2. Un punto C con coordenada z 8 se encuentra en el segmento de línea que une los puntos A (2, -3, 4) y B (8, 0, 10). Encuentra sus coordenadas.

Pregunta 3. Demuestra que tres puntos A(2, 3, 4), B(-1, 2, -3) y C(-4, 1, -10) son colineales y encuentra la razón en la que C divide a AB.

Pregunta 4. Encuentra la razón en la que la línea que une (2, 4, 5) y (3, 5, 4) se divide por el plano yz.

Pregunta 5. Halla la razón en que el segmento de recta que une los puntos (2, -1, 3) y (-1, 2, 1) se divide por el plano x+ y + z = 5.

Pregunta 6. Si los puntos A(3, 2, -4), B(9, 8, -10) y C(5, 4, -6) son colineales, encuentra la razón en la que C divide a AB.

Pregunta 7. Los puntos medios de los lados de un triángulo ABC están dados por (-2, 3, 5), (4, -1, 7) y (6, 5, 3). Encuentre las coordenadas de A, B y C.

Pregunta 8. A(1, 2, 3), B(0, 4, 1), C(-1, -1, -3) son los vértices de un triángulo ABC. Encuentra el punto en el que la bisectriz del ángulo ∠BAC intersecta a BC.

Pregunta 9. Halla la razón en que la esfera x2+y2 +z2 = 504 divide la recta que une los puntos (12, -4, 8) y (27, -9, 18).

Pregunta 10. Demostrar que el plano ax + by + cz + d = 0 divide la recta que une los puntos (x 1 ,y 1 ,z 1 ) y (x 2 ,y 2 ,z 2 ) en la razón

Pregunta 11. Encuentra el baricentro de un triángulo cuyos puntos medios son (1, 2, -3), (3, 0, 1) y (-1, 1, -4).

Pregunta 12. El baricentro de un triángulo ABC está en el punto (1, 1, 1). Si las coordenadas de A y B son (3, -5, 7) y (-1, 7, -6) respectivamente, encuentre las coordenadas del punto C.

Pregunta 13. Encuentra las coordenadas de los puntos que trisecan el segmento de recta que une los puntos P(4, 2, -6) y Q(10, -16, 6).

Pregunta 14. Usando la fórmula de la sección, demuestre que los puntos A(2, -3, 4), B(-1, 2, 1) y C(0, 1/3, 2) son colineales.

Pregunta 15. Dado que P(3, 2, -4), Q(5, 4, -6) y R(9, 8, -10) son colineales. Encuentra la razón en la que Q divide a PR.

Pregunta 16. Encuentra la razón en la que el segmento de línea que une los puntos (4, 8, 10) y (6, 10, -8) se divide por el plano yz.

Deja una respuesta Cancelar la respuesta

Pregunta 10. Demostrar que el plano ax + by + cz + d = 0 divide la recta que une los puntos (x ₁ ,y ₁ ,z ₁ ) y (x ₂ ,y ₂ ,z ₂ ) en la razón $\frac{ax_1+by_1+cz+d}{-ax_2+by_2+cz_2+d}$