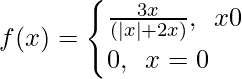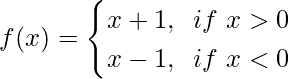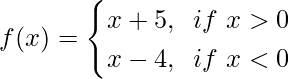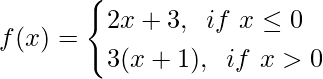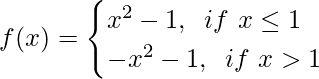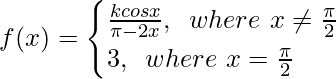Clase 11 RD Sharma Solutions – Capítulo 29 Límites – Ejercicio 29.1

Pregunta 1. Demuestra que Lim _x→0 (x/|x|) no existe.

Solución:

Tenemos, Lim _x→0 (x/|x|)

Ahora primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}\frac{x}{|x|}$

Sea x = 0 – h, donde h = 0

= $\lim_{h\to0^-}(\frac{(0 - h)}{|0 - h|})$

= $\lim_{h\to0^-}(\frac{(- h)}{h})$

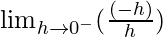
= -1

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to0^+}\frac{x}{|x|}$

Entonces, sea x = 0 + h, donde h = 0

= $\lim_{h\to0^+}(\frac{(0 + h)}{|0 + h|})$

= $\lim_{h\to0^+}(\frac{h}{h})$

= 1

Límite izquierdo ≠ Límite derecho

Entonces, Lim _x→0 (x/|x|) no existe.

Pregunta 2. Encuentra k para que Lim _x→0 f(x), donde 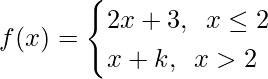$f(x)= \begin{cases} 2x+3, \hspace{0.2cm}x\le2\\ x+k,\hspace{0.2cm}x>2 \end{cases}$

Solución:

Tenemos, $f(x)= \begin{cases} 2x+3, \hspace{0.2cm}x\le2\\ x+k,\hspace{0.2cm}x>2 \end{cases}$

Ahora primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}(2x+3)$

Sea x = 2 – h, donde h= 0.

= $\lim_{h\to0^-}(2(2-h)+3)$

= [2(2 – 0) + 3]

= 7

Ahora encontramos el límite de la mano derecha:

$=\lim_{x\to0^+}f(x)$

= $\lim_{x\to0^+}(x+k)$

Sea x = 2 + h, donde h = 0

= $\lim_{h\to0^+}((2+h)+k)$

= (2 + 0) + k

= (2 + k)

Aquí, límite izquierdo = límite derecho, por lo que existe límite

Entonces, (2 + k) = 7

k = 5

Pregunta 3. Demuestra que Lim _x→0 (1/x) no existe.

Solución:

Tenemos que demostrar que Lim _x→0 (1/x) no existe

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}\frac{1}{x}$

Sea x = 0 – h, donde h = 0.

= $\lim_{h\to0^-}(\frac{1}{(0-h)})$

= $-\lim_{h\to0^-}(\frac{1}{h})$

= -∞

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to0^+}\frac{1}{x}$

Sea x = 0 + h, donde h = 0.

= $\lim_{h\to0^+}(\frac{1}{|(0+h)|})$

= $\lim_{h\to0^+}(\frac{1}{h})$

= ∞

Aquí, Límite izquierdo ≠ Límite derecho, por lo tanto, Lim _x→0 (1/x) no existe.

Pregunta 4. Sea f(x) una función definida por 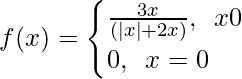$f(x)= \begin{cases} \frac{3x}{(|x|+2x)}, \hspace{0.2cm}x ≠ 0\\ 0,\hspace{0.2cm}x=0 \end{cases}$ . Demuestra que lim _x→0 f(x) no existe.

Solución:

Tenemos, $f(x)= \begin{cases} \frac{3x}{(|x|+2x)}, \hspace{0.2cm}x ≠ 0\\ 0,\hspace{0.2cm}x=0 \end{cases}$

De acuerdo con la pregunta tenemos que demostrar que lim _x→0 f(x) no existe.

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}\frac{3x}{|x|+2x}$

Sea x = 0 – h, donde h = 0

= $\lim_{h\to0^-}\frac{3(0-h)}{|0-h|+2(0-h)}$

= $\lim_{h\to0^-}(\frac{-3h}{h - 2h})$

= $\lim_{h\to0^-}(\frac{-3}{-1})$

= 3

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to0^+}\frac{3x}{|x|+2x}$

Sea x = 0 + h, donde h = 0.

= $\lim_{h\to0^+}\frac{3(0+h)}{|0+h|+2(0+h)}$

= $\lim_{h\to0^+}(\frac{3h}{3h})$

= $\lim_{h\to0^+}(\frac{3}{3})$

= 1

Aquí, Límite izquierdo ≠ Límite derecho, entonces, lím _x→0 f(x) no existe.

Pregunta 5. Sea 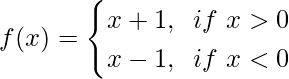$f(x)= \begin{cases} x+1, \hspace{0.2cm}if \ x >0\\ x-1,\hspace{0.2cm}if \ x<0 \end{cases}$ , Demuestre que lim _x→0 f(x) no existe.

Solución:

Tenemos, $f(x)= \begin{cases} x+1, \hspace{0.2cm}if \ x >0\\ x-1,\hspace{0.2cm}if \ x<0 \end{cases}$

Y tenemos que probar que lim _x→0 f(x) no existe.

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}(x-1)$

Sea x = 0 – h, donde h = 0.

= $\lim_{h\to0^-}((0-h)-1)$

= $\lim_{h\to0^-}(0-h-1)$

= -1

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to0^+}(x+1)$

Sea x = 0 + h, donde h = 0.

= $\lim_{h\to0^+}((0+h)+1)$

= $\lim_{h\to0^+}(0+h+1)$

= 1

Aquí, Límite izquierdo ≠ Límite derecho, entonces, lím _x→0 f(x) no existe.

Pregunta 6. Sea 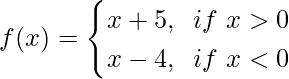$f(x)= \begin{cases} x+5, \hspace{0.2cm}if \ x >0\\ x-4,\hspace{0.2cm}if \ x<0 \end{cases}$ , Demuestre que lim _x→0 f(x) no existe.

Solución:

Tenemos, $f(x)= \begin{cases} x+5, \hspace{0.2cm}if \ x >0\\ x-4,\hspace{0.2cm}if \ x<0 \end{cases}$

Y tenemos que probar que lim _x→0 f(x) no existe.

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}(x-4)$

Sea x = 0 – h, donde h = 0.

= $\lim_{h\to0^-}((0-h)-4)$

= $\lim_{h\to0^-}(0-h-4)$

= -4

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to0^+}(x+5)$

Sea x = 0 + h, donde h = 0.

= $\lim_{h\to0^+}((0+h)+5)$

= $\lim_{h\to0^+}(0+h+5)$

= 5

Aquí, Límite izquierdo ≠ Límite derecho, entonces, lím _x→0 f(x) no existe.

Pregunta 7. Encuentra lim _x→3 f(x), donde 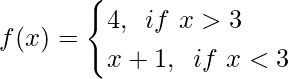$f(x)= \begin{cases} 4, \hspace{0.2cm}if \ x >3\\ x+1,\hspace{0.2cm}if \ x<3 \end{cases}$

Solución:

Tenemos, $f(x)= \begin{cases} 4, \hspace{0.2cm}if \ x >3\\ x+1,\hspace{0.2cm}if \ x<3 \end{cases}$

Y tenemos que encontrar lim _x→3 f(x)

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to3^-}(x+1)$

Sea x = 3 – h, donde h = 0.

= $\lim_{h\to0^-}((3-h)+1)$

= $\lim_{h\to0^-}(4-h)$

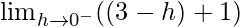
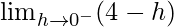
= 4

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to3^+}4$

Sea x = 3 + h, donde h = 0.

= $\lim_{h\to0^+}4$

= 4

Aquí, límite izquierdo = límite derecho,

Por lo tanto, lím _x→3 f(x) = 4

Pregunta 8(i). Si 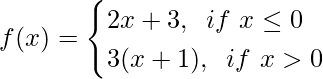$f(x)= \begin{cases} 2x+3, \hspace{0.2cm}if \ x\le0\\ 3(x+1),\hspace{0.2cm}if \ x>0 \end{cases}$ , encuentre lím _x→0 f(x).

Solución:

Tenemos, $f(x)= \begin{cases} 2x+3, \hspace{0.2cm}if \ x\le0\\ 3(x+1),\hspace{0.2cm}if \ x>0 \end{cases}$

Y tenemos que encontrar lim _x→0 f(x)

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}(2x+3)$

Sea x = 0 – h, donde h = 0.

= $\lim_{h\to0^-}(2(0-h)+3)$

= $\lim_{h\to0^-}(3-2h)$

= 3

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to0^+}3(x+1)$

Sea x = 0 + h, donde h = 0.

= $\lim_{h\to0^+}3((0+h)+1)$

= $\lim_{h\to0^+}(3+3h)$

= 3

Aquí, límite izquierdo = límite derecho,

Por lo tanto, lím _x→0 f(x) = 3

Pregunta 8(ii). Si 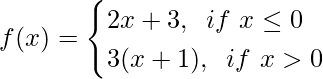$f(x)= \begin{cases} 2x+3, \hspace{0.2cm}if \ x\le0\\ 3(x+1),\hspace{0.2cm}if \ x>0 \end{cases}$ , encuentre lím _x→1 f(x).

Solución:

Tenemos, $f(x)= \begin{cases} 2x+3, \hspace{0.2cm}if \ x\le0\\ 3(x+1),\hspace{0.2cm}if \ x>0 \end{cases}$

Y tenemos que encontrar lim _x→1 f(x)

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to1^-}(2x+3)$

Sea x = 1 – h, donde h = 0.

= $\lim_{h\to0^-}(2(1-h)+3)$

= $\lim_{h\to0^-}(5-2h)$

= 5

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to1^+}3(x+1)$

Sea x = 1 + h, donde h = 0.

= $\lim_{h\to0^+}(3((1+h)+1))$

= $\lim_{h\to0^+}(6+3h)$

= 6

Aquí, Límite izquierdo ≠ Límite derecho, por lo que lím _x→1 f(x) no existe.

Pregunta 9. Encuentra lim _x→1 f(x) Donde 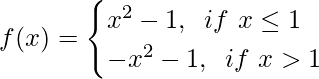$f(x)= \begin{cases} x^2-1, \hspace{0.2cm}if \ x\le1\\ -x^2-1,\hspace{0.2cm}if \ x>1 \end{cases}$

Solución:

Tenemos, $f(x)= \begin{cases} x^2-1, \hspace{0.2cm}if \ x\le1\\ -x^2-1,\hspace{0.2cm}if \ x>1 \end{cases}$

Y tenemos que encontrar lim _x→1 f(x)

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to1^-}(x^2-1)$

Sea x = 1 – h, donde h = 0.

= $\lim_{h\to0^-}((1-h)^2-1)$

= $\lim_{h\to0^-}(1-2h-h^2-1)$

= 0

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to1^+}(-x^2-1)$

Sea x = 1 + h, donde h = 0.

= $\lim_{h\to0^+}(-(1+h)^2-1)$

= $\lim_{h\to0^+}(-1-2h-h^2-1)$

= -2

Aquí, Límite izquierdo ≠ Límite derecho, entonces, lím _x→1 f(x) no existe.

Pregunta 10. Evalúa lím _x→0 f(x), donde 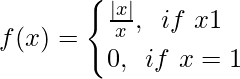$f(x)= \begin{cases} \frac{|x|}{x}, \hspace{0.2cm}if \ x≠1\\ 0,\hspace{0.2cm}if \ x=1 \end{cases}$

Solución:

Tenemos, $f(x)= \begin{cases} \frac{|x|}{x}, \hspace{0.2cm}if \ x≠1\\ 0,\hspace{0.2cm}if \ x=1 \end{cases}$

Y tenemos que encontrar lim _x→0 f(x)

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}\frac{|x|}{x}$

Sea x = 0 – h, donde h = 0.

= $\lim_{h\to0^-}\frac{|0-h|}{0-h}$

= $\lim_{h\to0^-}(\frac{h}{-h})$

= -1

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to0^+}\frac{|x|}{x}$

Sea x = 0 + h, donde h = 0.

= $\lim_{h\to0^+}\frac{|0+h|}{0+h}$

= $\lim_{h\to0^+}(\frac{h}{h})$

= 1

Aquí, Límite izquierdo ≠ Límite derecho, entonces, lím _x→0 f(x) no existe.

Pregunta 11. Sea a ₁ , a ₂ ,……….a _n un número real fijo tal que f(x) = (x – a ₁ )(x – a ₂ )……..(xa _n ). ¿Qué es lím _x→a1 f(x)? Calcule lím _x→a f(x).

Solución:

Tenemos, f(x) = (x – a ₁ )(x – a ₂ )……..(x – a _n )

$\lim_{x→a_1}f(x)=\lim_{x→a_1}[(x-a_1)(x-a_2)........(x-a_n)]$

Ahora pon x = a ₁

= (a ₁ – a ₁ )(a ₁ – a ₂ )……..(a ₁ – a _n )

= 0

Ahora, lím _x→a f(x) = lím _x→a [(x – a ₁ )(x – a ₂ )……..(x – a _n )]

Ahora pon x = a

= (a – a ₁ )(a – a ₂ )……..(a – a _n )

Por lo tanto, lim _x→a f(x) = (a – a ₁ )(a – a ₂ )……..(a – a _n )

Pregunta 12. Encuentra lim _{x→1 ⁺} [1/(x – 1)].

Solución:

Tenemos que encontrar lim _{x→1 ⁺} [1/(x – 1)]

= $\lim_{x\to1^+}\frac{1}{x-1}$

Sea x = 1 + h, donde h = 0.

= $\lim_{h\to0^+}\frac{1}{(1+h)-1}$

= $\lim_{h\to0^+}\frac{1}{(h)}$

= ∞

Por lo tanto, lim _{x→1 ⁺} [1/(x – 1)] = ∞

Pregunta 13(i). Evalúa los siguientes límites unilaterales: lím _{x→2 ⁺} [(x – 3)/(x ² – 4)]

Solución:

Tenemos, $\lim_{x\to2^+}\frac{x-3}{x^2-4}$

Sea x = 2 + h, donde h = 0.

= $\lim_{h\to0^+}(\frac{(2+h)-3}{(2+h)^2-4})$

= $\lim_{h\to0^+}(\frac{h-1}{4+4h+h^2-4})$

= $\lim_{h\to0^+}(\frac{h-1}{4h+h^2})$

= -∞

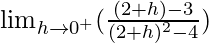
Pregunta 13(ii). Evalúe los siguientes límites unilaterales: lím _{x→2 ^–} [(x – 3)/(x ² – 4)]

Solución:

Tenemos, $\lim_{x\to2^-}\frac{x-3}{x^2-4}$

Sea x = 2 – h, donde h = 0.

= $\lim_{h\to0^-}\frac{(2-h)-3}{(2-h)^2-4}$

= $\lim_{h\to0^-}\frac{(-h-1)}{4-4h+h^2-4}$

= $\lim_{h\to0^-}\frac{(-h-1)}{-4h+h^2}$

= ∞

Pregunta 13(iii). Evalúe los siguientes límites unilaterales: lím _{x→0 ⁺} [1/3x]

Solución:

Tenemos, lím _{x→0 ⁺} [1/3x]

Sea x = 0 + h, donde h = 0.

= Límite _{h→0 ⁺} [1/3(0+h)]

= Límite _{h→0 ⁺} [1/(3h)]

= ∞

Pregunta 13(iv). Evalúa los siguientes límites unilaterales: lím _{x→-8 ⁺} [2x/(x + 8)]

Solución:

Tenemos, límite _{x→-8 ⁺} [2x/(x + 8)]

Sea x = -8 + h, donde h = 0.

= límitex _{→0 ⁺} [2(-8 + h)/(-8 + h + 8)]

= Límite _{h→0 ⁺} [(2h – 16)/(h)]

= -∞

Pregunta 13(v). Evalúa los siguientes límites unilaterales: lim _{x→0 ⁺} [2/x ^1/5 ]

Solución:

Tenemos, lim _{x→0 ⁺} [2/x ^1/5 ]

Sea x = 0 + h, donde h = 0.

= Lím _{h→0 ⁺} [2/(0 + h) ^1/5 ]

= ∞

Pregunta 13 (vi). Evalúa los siguientes límites unilaterales: lím _{x→(π/2) ^–} [tanx]

Solución:

Tenemos, lim _{x→(π/2) ^–} [tanx]

Sea x = 0 – h, donde h = 0.

= lím _{h→0 ^–} [tan(π/2 – h)]

= lím _{x→0 ^–} [cot h]

= ∞

Pregunta 13 (vii). Evalúa los siguientes límites unilaterales: lím _{x→(-π/2) ⁺} [secx]

Solución:

Tenemos, lim _{x→(-π/2) ⁺} [secx]

Sea x = 0 + h, donde h = 0.

= lím _{h→0 ⁺} [secx(-π/2 + h)]

= lím _{h→0 ⁺} [cosec h]

= ∞

Pregunta 13 (viii). Evalúe los siguientes límites unilaterales: lím _{x→0 ^–} [(x ² – 3x + 2)/x ³ – 2x ² ]

Solución:

Tenemos, lim _x→0 -[x ² – 3x + 2/x ³ – 2x ² ]

= Lim _x→0 -[(x – 1)(x – 2)/x ² (x – 2)]

= Límite _x→0 -[(x – 1)/x ² ]

Sea x = 0 – h, donde h = 0.

= Lim _h→0 -[(0 – h – 1)/(0 – h) ² ]

= -∞

Pregunta 13(ix). Evalúa los siguientes límites unilaterales: lím _{x→-2 ⁺} [(x ² – 1)/(2x + 4)]

Solución:

Tenemos, límite _{x→-2 ⁺} [(x ² – 1)/(2x + 4)]

Sea x = -2 + h, donde h = 0.

= Lim _h→-0⁺ [(-2 + h) ² – 1)/2(-2 + h) + 4]

= Lim _h→-0⁺ [(-2 + h) ² – 1)/(-4 + 4 + h)]

= (4 – 1)/0

= ∞

Pregunta 13(x). Evalúa los siguientes límites unilaterales: lim _x→0 -[2 – cotx]

Solución:

Tenemos, lim _x→0 -[2 – cotx]

Sea x = 0 – h, donde h = 0.

= Lim _h→0 -[2 – cot(0 – h)]

= Lim _h→0 -[2 + cot(h)]

= 2 + ∞

= ∞

Pregunta 13(xi). Evalúe los siguientes límites unilaterales. lím _x→0 -[1 + cosecx]

Solución:

Tenemos, lim _x→0 -[1 + cosecx]

Sea x = 0 – h, donde h = 0.

= Lim _h→0 -[1 + cosec(0 – h)]

= Lim _h→0 -[1 – cosec(h)]

= 1 – ∞

= -∞

Pregunta 14. Demuestra que Lim _x→0 e ^-1/x no existe.

Solución:

Sea, f(x) = Lim _x→0 e ^-1/x

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}e^{-\frac{1}{x}}$

Sea x = 0 – h, donde h = 0.

= $\lim_{h\to0^-}e^{-\frac{1}{0-h}}$

= $\lim_{h\to0^-}e^{\frac{1}{h}}$

= mi ^∞

= ∞

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to0^+}e^{-\frac{1}{x}}$

Sea x = 0 + h, donde h = 0.

= $\lim_{h\to0^+}e^{-\frac{1}{0 + h}}$

= $\lim_{h\to0^+}e^{-\frac{1}{h}}$

= mi- ^∞

= 0

Aquí, límite izquierdo ≠ límite derecho, entonces, Lim _x→0 e ^-1/x no existe.

Pregunta 15(i). Hallar límite _x→2 [x]

Solución:

Tenemos, Lim _x→2 [x], donde [] es la mayor función entera

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}[x]$

Sea x = 2 – h, donde h = 0.

= $\lim_{h\to0^-}[2 - h]$

= 1

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to0^+}[x]$

Sea x = 2 + h, donde h = 0.

= $\lim_{h\to0^+}[2+h]$

= 2

Aquí, Límite izquierdo ≠ Límite derecho, por lo tanto, Lim _x→2 [x] no existe.

Pregunta 15(ii). Encuentre Lim _x→5/2 [x]

Solución:

Tenemos, Lim _x→2 [x], donde [] es la mayor función entera

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to\frac{5}{2}^-}[x]$

Sea x = 5/2 – h, donde h = 0.

= $\lim_{h\to0^-}[\frac{5}{2} - h]$

= 2

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to\frac{5}{2}^+}[x]$

Sea x = 5/2 + h, donde h = 0.

= $\lim_{h\to0^+}[\frac{5}{2}+h]$

= 2

Aquí, límite izquierdo = límite derecho, entonces, Lim _x→5/2 [x] = 2

Pregunta 15(iii). Hallar límite _x→1 [x]

Solución:

Tenemos, Lim _x→1 [x], donde [] es la mayor función entera

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to1^-}[x]$

Sea x = 1 – h, donde h = 0.

= $\lim_{h\to0^-}[1-h]$

= 0

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to1^+}[x]$

Sea x = 1 + h, donde h = 0.

= $\lim_{h\to0^+}[1+h]$

= 1

Aquí, límite izquierdo = límite derecho, entonces, Lim _x→1 [x] no existe.

Pregunta 16. Demuestra que Lim _x→a+ [x] = [a]. Demuestra también que Lim _x→1 -[x] = 0.

Solución:

Tenemos, $\lim_{x\to a^+}[x]$

Sea x = a + h, donde h = 0.

= Lím _h→0 -[(a + h)]

= un

También, $\lim_{x\to1^-}[x]$

Sea x = 1 – h, donde h = 0.

= Límite _h→0 [(1 – h)]

= 0

Pregunta 17. Demuestra que Lim _x→2 +(x/[x]) ≠ Lim _x→2 -(x/[x]).

Solución:

Tenemos que mostrar Lim _x→2 +(x/[x]) ≠ Lim _x→2 -(x/[x])

Entonces, RHL

Tenemos, $\lim_{x\to2^-}\frac{x}{[x]}$ , donde [] es la mayor función entera

Sea x = 2 – h, donde h = 0.

= Lím _h→0 -[(2 – h)/|[2 – h]]

= 2/1

= 2

Ahora LHL

Tenemos, $\lim_{x\to2^+}\frac{x}{[x]}$ , donde [] es la mayor función entera

Sea x = 2 + h, donde h = 0.

= Lim _h→0 +[(2 + h)/|[2 + h]]

= 2/2

= 1

Por lo tanto, límite izquierdo≠límite derecho

Pregunta 18. Encuentra Lim _x→3 +(x/[x]). ¿Es igual a Lim _x→3 -(x/[x])

Solución:

Tenemos, $\lim_{x\to3^-}\frac{x}{[x]}$ donde [] es la función entera más grande

Sea x = 3 – h, donde h = 0.

= Lim _h→0 -[(3 – h)/|[3 – h]]

= 3/2

También, $\lim_{x\to3^+}\frac{x}{[x]}$

Sea x = 3 + h, donde h = 0.

= Lim _h→0 +[(3 + h)/|[3 + h]]

= 3/3

= 1

Por lo tanto, límite izquierdo≠límite derecho

Pregunta 19. Encuentra Lim _x→5/2 [x]

Solución:

Tenemos que encontrar Lim _x→5/2 [x], donde [] es la mayor función entera

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to\frac{5}{2}^-}[x]$

Sea x = 5/2 – h, donde h = 0.

= Lím _h→0 -[(5/2 – h)]

= 2

Ahora encontramos el límite de la mano derecha:

$=\lim_{x\to\frac{5}{2}^+}[x]$

Sea x = 5/2 + h, donde h = 0.

= Lím _h→0 +[(5/2+h)]

= 2

Por lo tanto, límite izquierdo = límite derecho, entonces Lim _x→5/2 [x] = 2

Pregunta 20. Evalúa Lim _x→2 f(x), donde $f(x)= \begin{cases} x-[x], \hspace{0.2cm}x<2\\ 4 , \hspace{0.2cm}x=2\\ x+k,\hspace{0.2cm}x>2 \end{cases}$

Solución:

Tenemos, $f(x)= \begin{cases} x-[x], \hspace{0.2cm}x<2\\ 4 , \hspace{0.2cm}x=2\\ x+k,\hspace{0.2cm}x>2 \end{cases}$

Tenemos que encontrar Lim _x→2 f(x)

entonces por eso

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}(x-[x])$

Sea x = 2 – h, donde h = 0.

= Lim _h→0 -{(2 – h) – [2 – h]}

= 2 – 1

= 1

Ahora encontramos el límite de la mano derecha:

= $\lim_{x\to2^+}(3x-5)$

Sea x = 2 + h, donde h = 0.

= Lím _h→0 -[3(2 + h) – 5]

= 6 – 5

= 1

Por lo tanto, límite izquierdo = límite derecho, entonces, Lim _x→2 f(x) = 1

Pregunta 21. Demuestra que Lim _x→0 sin(1/x) no existe.

Solución:

Sea, f(x) = Lim _x→0 sin(1/x)

Primero encontramos el límite izquierdo:

= $\lim_{x\to0^-}sin\frac{1}{x}$

Sea x = 0 – h, donde h = 0.

= Lim _h→0 sen[1/(0 – h)]

= -Lim _h→0 sen[1/(h)]

Un número oscilante se encuentra entre -1 y +1.

Entonces el límite de la mano izquierda no existe.

De manera similar, el límite de la derecha también oscila.

Entonces, Lim _x→0 sin(1/x) no existe.

Pregunta 22. Sea 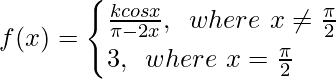$f(x)= \begin{cases} \frac{kcosx}{\pi-2x}, \hspace{0.2cm}where \ x \neq \frac{\pi}{2}\\ 3,\hspace{0.2cm}where \ x =\frac{\pi}{2} \end{cases}$ y si lim _x→

Solución:

Tenemos $f(x)= \begin{cases} \frac{kcosx}{\pi-2x}, \hspace{0.2cm}where \ x \neq \frac{\pi}{2}\\ 3,\hspace{0.2cm}where \ x =\frac{\pi}{2} \end{cases}$

Primero encontramos el límite izquierdo:

= $\lim_{x\to\frac{\pi}{2}^-}\frac{kcosx}{\pi-2x}$

Sea x = – h, donde h = 0.

= $\lim_{h\to0^-}\frac{kcos(\frac{\pi}{2}-h)}{\pi-2(\frac{\pi}{2}-h)}$

= k cos()/

= k/

Ahora encontramos el límite de la mano derecha:

$\lim_{x\to\frac{\pi}{2}^+}\frac{kcosx}{\pi-2x}$

Sea x = + h, donde h = 0.

= $\lim_{h\to0^+}\frac{kcos(\frac{\pi}{2}+h)}{\pi-2(\frac{\pi}{2}+h)}$

= k cos()/-

= k/

Por lo tanto, límite izquierdo = límite derecho, entonces

límite _x→

k/

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Demuestra que Lim x→0 (x/|x|) no existe.

Pregunta 2. Encuentra k para que Lim x→0 f(x), donde

Pregunta 3. Demuestra que Lim x→0 (1/x) no existe.

Pregunta 4. Sea f(x) una función definida por . Demuestra que lim x→0 f(x) no existe.

Pregunta 5. Sea , Demuestre que lim x→0 f(x) no existe.

Pregunta 7. Encuentra lim x→3 f(x), donde

Pregunta 8(i). Si , encuentre lím x→0 f(x).

Pregunta 8(ii). Si , encuentre lím x→1 f(x).

Pregunta 9. Encuentra lim x→1 f(x) Donde

Pregunta 10. Evalúa lím x→0 f(x), donde

Pregunta 11. Sea a 1 , a 2 ,……….a n un número real fijo tal que f(x) = (x – a 1 )(x – a 2 )……..(xa n ). ¿Qué es lím x→a1 f(x)? Calcule lím x→a f(x).

Pregunta 12. Encuentra lim x→1 + [1/(x – 1)].

Pregunta 13(i). Evalúa los siguientes límites unilaterales: lím x→2 + [(x – 3)/(x 2 – 4)]

Pregunta 13(ii). Evalúe los siguientes límites unilaterales: lím x→2 – [(x – 3)/(x 2 – 4)]

Pregunta 13(iii). Evalúe los siguientes límites unilaterales: lím x→0 + [1/3x]

Pregunta 13(iv). Evalúa los siguientes límites unilaterales: lím x→-8 + [2x/(x + 8)]

Pregunta 13(v). Evalúa los siguientes límites unilaterales: lim x→0 + [2/x 1/5 ]

Pregunta 13 (vi). Evalúa los siguientes límites unilaterales: lím x→(π/2) – [tanx]

Pregunta 13 (vii). Evalúa los siguientes límites unilaterales: lím x→(-π/2) + [secx]

Pregunta 13 (viii). Evalúe los siguientes límites unilaterales: lím x→0 – [(x 2 – 3x + 2)/x 3 – 2x 2 ]

Pregunta 13(ix). Evalúa los siguientes límites unilaterales: lím x→-2 + [(x 2 – 1)/(2x + 4)]

Pregunta 13(x). Evalúa los siguientes límites unilaterales: lim x→0 -[2 – cotx]

Pregunta 13(xi). Evalúe los siguientes límites unilaterales. lím x→0 -[1 + cosecx]

Pregunta 14. Demuestra que Lim x→0 e -1/x no existe.

Pregunta 15(i). Hallar límite x→2 [x]

Pregunta 15(ii). Encuentre Lim x→5/2 [x]

Pregunta 15(iii). Hallar límite x→1 [x]

Pregunta 16. Demuestra que Lim x→a+ [x] = [a]. Demuestra también que Lim x→1 -[x] = 0.

Pregunta 17. Demuestra que Lim x→2 +(x/[x]) ≠ Lim x→2 -(x/[x]).

Pregunta 18. Encuentra Lim x→3 +(x/[x]). ¿Es igual a Lim x→3 -(x/[x])

Pregunta 19. Encuentra Lim x→5/2 [x]

Pregunta 20. Evalúa Lim x→2 f(x), donde

Pregunta 21. Demuestra que Lim x→0 sin(1/x) no existe.

Pregunta 22. Sea y si lim x→

Deja una respuesta Cancelar la respuesta

Pregunta 1. Demuestra que Lim _x→0 (x/|x|) no existe.

Pregunta 2. Encuentra k para que Lim _x→0 f(x), donde $f(x)= \begin{cases} 2x+3, \hspace{0.2cm}x\le2\\ x+k,\hspace{0.2cm}x>2 \end{cases}$

Pregunta 3. Demuestra que Lim _x→0 (1/x) no existe.

Pregunta 4. Sea f(x) una función definida por $f(x)= \begin{cases} \frac{3x}{(|x|+2x)}, \hspace{0.2cm}x ≠ 0\\ 0,\hspace{0.2cm}x=0 \end{cases}$ . Demuestra que lim _x→0 f(x) no existe.

Pregunta 5. Sea $f(x)= \begin{cases} x+1, \hspace{0.2cm}if \ x >0\\ x-1,\hspace{0.2cm}if \ x<0 \end{cases}$ , Demuestre que lim _x→0 f(x) no existe.

Pregunta 7. Encuentra lim _x→3 f(x), donde $f(x)= \begin{cases} 4, \hspace{0.2cm}if \ x >3\\ x+1,\hspace{0.2cm}if \ x<3 \end{cases}$

Pregunta 8(i). Si $f(x)= \begin{cases} 2x+3, \hspace{0.2cm}if \ x\le0\\ 3(x+1),\hspace{0.2cm}if \ x>0 \end{cases}$ , encuentre lím _x→0 f(x).

Pregunta 8(ii). Si $f(x)= \begin{cases} 2x+3, \hspace{0.2cm}if \ x\le0\\ 3(x+1),\hspace{0.2cm}if \ x>0 \end{cases}$ , encuentre lím _x→1 f(x).

Pregunta 9. Encuentra lim _x→1 f(x) Donde $f(x)= \begin{cases} x^2-1, \hspace{0.2cm}if \ x\le1\\ -x^2-1,\hspace{0.2cm}if \ x>1 \end{cases}$

Pregunta 10. Evalúa lím _x→0 f(x), donde $f(x)= \begin{cases} \frac{|x|}{x}, \hspace{0.2cm}if \ x≠1\\ 0,\hspace{0.2cm}if \ x=1 \end{cases}$

Pregunta 11. Sea a ₁ , a ₂ ,……….a _n un número real fijo tal que f(x) = (x – a ₁ )(x – a ₂ )……..(xa _n ). ¿Qué es lím _x→a1 f(x)? Calcule lím _x→a f(x).

Pregunta 12. Encuentra lim _{x→1 ⁺} [1/(x – 1)].

Pregunta 13(i). Evalúa los siguientes límites unilaterales: lím _{x→2 ⁺} [(x – 3)/(x ² – 4)]

Pregunta 13(ii). Evalúe los siguientes límites unilaterales: lím _{x→2 ^–} [(x – 3)/(x ² – 4)]

Pregunta 13(iii). Evalúe los siguientes límites unilaterales: lím _{x→0 ⁺} [1/3x]

Pregunta 13(iv). Evalúa los siguientes límites unilaterales: lím _{x→-8 ⁺} [2x/(x + 8)]

Pregunta 13(v). Evalúa los siguientes límites unilaterales: lim _{x→0 ⁺} [2/x ^1/5 ]

Pregunta 13 (vi). Evalúa los siguientes límites unilaterales: lím _{x→(π/2) ^–} [tanx]

Pregunta 13 (vii). Evalúa los siguientes límites unilaterales: lím _{x→(-π/2) ⁺} [secx]

Pregunta 13 (viii). Evalúe los siguientes límites unilaterales: lím _{x→0 ^–} [(x ² – 3x + 2)/x ³ – 2x ² ]

Pregunta 13(ix). Evalúa los siguientes límites unilaterales: lím _{x→-2 ⁺} [(x ² – 1)/(2x + 4)]

Pregunta 13(x). Evalúa los siguientes límites unilaterales: lim _x→0 -[2 – cotx]

Pregunta 13(xi). Evalúe los siguientes límites unilaterales. lím _x→0 -[1 + cosecx]

Pregunta 14. Demuestra que Lim _x→0 e ^-1/x no existe.

Pregunta 15(i). Hallar límite _x→2 [x]

Pregunta 15(ii). Encuentre Lim _x→5/2 [x]

Pregunta 15(iii). Hallar límite _x→1 [x]

Pregunta 16. Demuestra que Lim _x→a+ [x] = [a]. Demuestra también que Lim _x→1 -[x] = 0.

Pregunta 17. Demuestra que Lim _x→2 +(x/[x]) ≠ Lim _x→2 -(x/[x]).

Pregunta 18. Encuentra Lim _x→3 +(x/[x]). ¿Es igual a Lim _x→3 -(x/[x])

Pregunta 19. Encuentra Lim _x→5/2 [x]

Pregunta 20. Evalúa Lim _x→2 f(x), donde $f(x)= \begin{cases} x-[x], \hspace{0.2cm}x<2\\ 4 , \hspace{0.2cm}x=2\\ x+k,\hspace{0.2cm}x>2 \end{cases}$

Pregunta 21. Demuestra que Lim _x→0 sin(1/x) no existe.

Pregunta 22. Sea $f(x)= \begin{cases} \frac{kcosx}{\pi-2x}, \hspace{0.2cm}where \ x \neq \frac{\pi}{2}\\ 3,\hspace{0.2cm}where \ x =\frac{\pi}{2} \end{cases}$ y si lim _x→