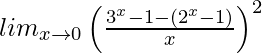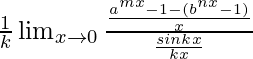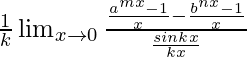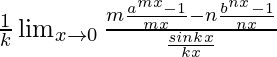Clase 11 RD Sharma Solutions – Capítulo 29 Límites – Ejercicio 29.10 | Serie 1

Posted on by Rudeus Greyrat

Evalúa los siguientes límites:

Pregunta 1. 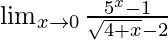\lim_{x\to0}\frac{5^x-1}{\sqrt{4+x}-2}

Solución:

Tenemos,

=\lim_{x\to0}\frac{5^x-1}{\sqrt{4+x}-2}

=\lim_{x\to0}\frac{(5^x-1)(\sqrt{4+x}+2)}{(\sqrt{4+x}-2)(\sqrt{4+x}+2)}

=\lim_{x\to0}\frac{(5^x-1)(\sqrt{4+x}+2)}{4+x-4}

=\lim_{x\to0}\frac{(5^x-1)(\sqrt{4+x}+2)}{x}

=\lim_{x\to0}\frac{(5^x-1)}{x}\lim_{x\to0}(\sqrt{4+x}+2)

=4\lim_{x\to0}\frac{(5^x-1)}{x}

Sabemos, lim_{x\to0}\frac{a^x-1}{x}=loga . Entonces tenemos,

= 4 registro 5

Pregunta 2. 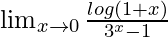\lim_{x\to0}\frac{log(1+x)}{3^x-1}

Solución:

Tenemos,

=\lim_{x\to0}\frac{log(1+x)}{3^x-1}

=\lim_{x\to0}\frac{log(1+x)}{x}×\frac{1}{\lim_{x\to0}\frac{3^x-1}{x}}

Sabemos, lim_{x\to0}\frac{log(1+x)}{x}=1 . Entonces tenemos,

=\frac{1}{\lim_{x\to0}\frac{3^x-1}{x}}

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

=\frac{1}{log3}

Pregunta 3. 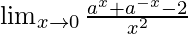\lim_{x\to0}\frac{a^x+a^{-x}-2}{x^2}

Solución:

Tenemos,

=\lim_{x\to0}\frac{a^x+a^{-x}-2}{x^2}

=\lim_{x\to0}\frac{a^{2x}+1-2a^x}{x^2}

=\lim_{x\to0}(\frac{a^x-1}{x})^2×\frac{1}{a^x}

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

=(log_ea)^2×\frac{1}{a^0}

= (log e a) 2

Pregunta 4. 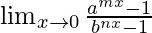 \lim_{x\to0}\frac{a^{mx}-1}{b^{nx}-1} , n≠0

Solución:

Tenemos,

=\lim_{x\to0}\frac{a^{mx}-1}{b^{nx}-1}

=\lim_{x\to0}\frac{a^{mx}-1}{mx}×\frac{1}{\lim_{x\to0}\frac{b^{nx}-1}{nx}}×\frac{m}{n}

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

=loga×\frac{1}{logb}×\frac{m}{n}

=\frac{mloga}{nlogb}

Pregunta 5. 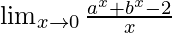\lim_{x\to0}\frac{a^x+b^x-2}{x}

Solución:

Tenemos,

=\lim_{x\to0}\frac{a^x+b^x-2}{x}

=\lim_{x\to0}\frac{(a^x-1)+(b^x-1)}{x}

=\lim_{x\to0}\left(\frac{a^x-1}{x}+\frac{b^x-1}{x}\right)

=\lim_{x\to0}\frac{a^x-1}{x}+\lim_{x\to0}\frac{b^x-1}{x}

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

= registro a + registro b

= registro (ab)

Pregunta 6. 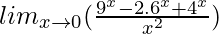lim_{x\to0}(\frac{9^x-2.6^x+4^x}{x^2})

Solución:

Tenemos,

=lim_{x\to0}(\frac{9^x-2.6^x+4^x}{x^2})

=lim_{x\to0}\frac{(3^x)^2-2.6^x+(2^x)^2}{x^2}

=lim_{x\to0}\left(\frac{3^x-2^x}{x}\right)^2

=lim_{x\to0}\left(\frac{3^x-1-(2^x-1)}{x}\right)^2

=lim_{x\to0}\left(\frac{3^x-1}{x}-\frac{2^x-1}{x}\right)^2

=\left(lim_{x\to0}\frac{3^x-1}{x}-lim_{x\to0}\frac{2^x-1}{x}\right)^2

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

= (registro 3 − registro 2) 2

=\left(log\frac{3}{2}\right)^2

Pregunta 7. 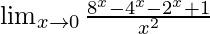\lim_{x\to0}\frac{8^x-4^x-2^x+1}{x^2}

Solución:

Tenemos,

=\lim_{x\to0}\frac{8^x-4^x-2^x+1}{x^2}

=\lim_{x\to0}\frac{(2^x-1)^2(2^x+1)}{x^2}

=\lim_{x\to0}\frac{(2^x-1)^2}{{x^2}}×\lim_{x\to0}(2^x+1)

=2\lim_{x\to0}\left(\frac{2^x-1}{x}\right)^2

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

= 2(log2) 2

pregunta 8 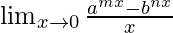\lim_{x\to0}\frac{a^{mx}-b^{nx}}{x}

Solución:

Tenemos,

=\lim_{x\to0}\frac{a^{mx}-b^{nx}}{x}

=\lim_{x\to0}\frac{(a^{mx}-1)-(b^{nx}-1)}{x}

=\lim_{x\to0}\left(\frac{a^{mx}-1}{x}-\frac{b^{nx}-1}{x}\right)

=\lim_{x\to0}\left(m×\frac{a^{mx}-1}{mx}\right)-\lim_{x\to0}\left(n×\frac{b^{nx}-1}{nx}\right)

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

= metro log a – n log b

= iniciar sesión un metro – iniciar sesión segundo norte

=log\left(\frac{a^m}{b^n}\right)

Pregunta 9. 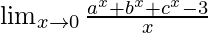\lim_{x\to0}\frac{a^x+b^x+c^x-3}{x}

Solución:

Tenemos,

=\lim_{x\to0}\frac{a^x+b^x+c^x-3}{x}

=\lim_{x\to0}\frac{(a^x-1)+(b^x-1)+(c^x-1)}{x}

=\lim_{x\to0}\frac{a^x-1}{x}+\lim_{x\to0}\frac{b^x-1}{x}+\lim_{x\to0}\frac{c^x-1}{x}

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

= log a + log b + log c

= registro (abc)

Pregunta 10. 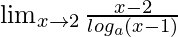\lim_{x\to2}\frac{x-2}{log_a(x-1)}

Solución:

Tenemos,

=\lim_{x\to2}\frac{x-2}{log_a(x-1)}

Sea x − 2 = h. Entonces, obtenemos,

=\lim_{h\to0}\frac{h}{log_a(h+1)}

=\lim_{h\to0}\frac{h}{\frac{log(h+1)}{loga}}

=\lim_{h\to0}\frac{loga}{\frac{log(h+1)}{h}}

=\frac{loga}{\lim_{h\to0}\frac{log(h+1)}{h}}

Sabemos, lim_{x\to{a}}\frac{log(1+x)}{x}=1 . Entonces tenemos,

= registrar un

Pregunta 11. 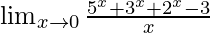\lim_{x\to0}\frac{5^x+3^x+2^x-3}{x}

Solución:

Tenemos,

=\lim_{x\to0}\frac{5^x+3^x+2^x-3}{x}

=\lim_{x\to0}\frac{(5^x-1)+(3^x-1)+(2^x-1)}{x}

=\lim_{x\to0}\frac{5^x-1}{x}+\lim_{x\to0}\frac{4^x-1}{x}+\lim_{x\to0}\frac{3^x-1}{x}

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

= registro 5 + registro 3 + registro 2

= logaritmo (5×3×2)

= registro 30

Pregunta 12. \lim_{x\to0}(a^{\frac{1}{x}}-1)x

Solución:

Tenemos,

=\lim_{x\to0}(a^{\frac{1}{x}}-1)x

Sea 1/x = h. Obtenemos,

=\lim_{h\to0}(a^h-1)\frac{1}{h}

=\lim_{h\to0}\frac{a^h-1}{h}

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

= registrar un

Pregunta 13. 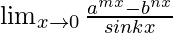\lim_{x\to0}\frac{a^{mx}-b^{nx}}{sinkx}

Solución:

Tenemos,

=\lim_{x\to0}\frac{a^{mx}-b^{nx}}{sinkx}

=\lim_{x\to0}\frac{a^{mx}-b^{nx}}{kx×\frac{sinkx}{kx}}

=\frac{1}{k}\lim_{x\to0}\frac{\frac{a^{mx}-b^{nx}}{x}}{\frac{sinkx}{kx}}

=\frac{1}{k}\lim_{x\to0}\frac{\frac{a^{mx}-1-(b^{nx}-1)}{x}}{\frac{sinkx}{kx}}

=\frac{1}{k}\lim_{x\to0}\frac{\frac{a^{mx}-1}{x}-\frac{b^{nx}-1}{x}}{\frac{sinkx}{kx}}

=\frac{1}{k}\lim_{x\to0}\frac{m×\frac{a^{mx}-1}{mx}-n×\frac{b^{nx}-1}{nx}}{\frac{sinkx}{kx}}

Como lim_{x\to0}\frac{a^x-1}{x}=loga y lim_{x\to0}\frac{sinx}{x}=1 , obtenemos,

=\frac{mloga-nlogb}{k}

=\frac{loga^m-logb^n}{k}

=\frac{1}{k}log(\frac{a^m}{b^n})

Pregunta 14. 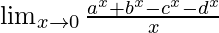\lim_{x\to0}\frac{a^x+b^x-c^x-d^x}{x}

Solución:

Tenemos,

=\lim_{x\to0}\frac{a^x+b^x-c^x-d^x}{x}

=\lim_{x\to0}\frac{(a^x-1)+(b^x-1)-(c^x-1)-(d^x-1)}{x}

=\lim_{x\to0}\frac{a^x-1}{x}+\lim_{x\to0}\frac{b^x-1}{x}-\lim_{x\to0}\frac{c^x-1}{x}-\lim_{x\to0}\frac{d^x-1}{x}

Como lim_{x\to0}\frac{a^x-1}{x}=loga , obtenemos,

= log a + log b − log c − log d

= log a+ log b − (log c + log d)

= registro ab − registro cd

=\frac{ab}{cd}

Pregunta 15. \lim_{x\to0}\frac{e^x-1+sinx}{x}

Solución:

Tenemos,

=\lim_{x\to0}\frac{e^x-1+sinx}{x}

=\lim_{x\to0}\frac{e^x-1}{x}+\lim_{x\to0}\frac{sinx}{x}

Como lim_{x\to0}\frac{a^x-1}{x}=loga y lim_{x\to0}\frac{sinx}{x}=1 , obtenemos,

= registro e + 1

= 1 + 1

= 2

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *