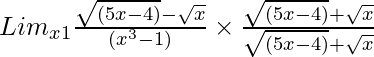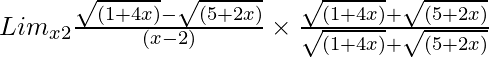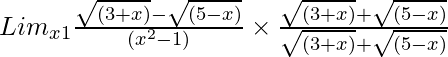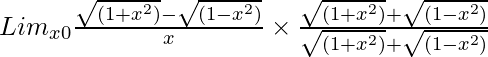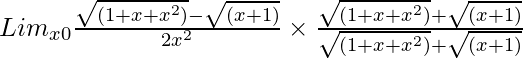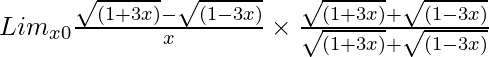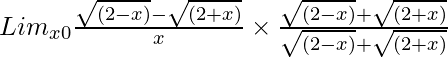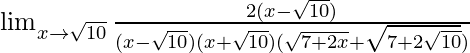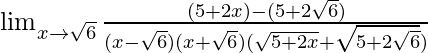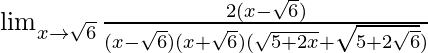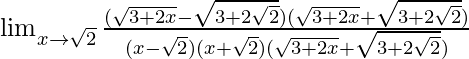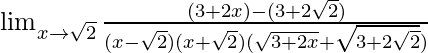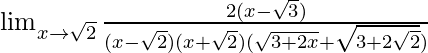Clase 11 RD Sharma Solutions – Capítulo 29 Límites – Ejercicio 29.4

Evalúa los siguientes límites:

Pregunta 18. Lim _x→1 {√(5x – 4) – √x}/(x ³ – 1)

Solución:

Tenemos, Lim _x→1 {√(5x – 4) – √x}/(x ³ – 1)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 1, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→1}\frac{\sqrt{(5x - 4)} - \sqrt{x}}{(x^3 - 1)} \times \frac{\sqrt{(5x - 4)} + \sqrt{x}}{\sqrt{(5x - 4)} + \sqrt{x}}$

= Lim _x→1 {(5x – 4) – x}/[{√(5x – 4) + √x}(x ³ – 1)]

= Lim _x→1 {4(x – 1)}/[{√(5x – 4) + √x}(x-1)(x ² + x + 1)]

= Lim _x→1 (4)/[{√(5x – 4) + √x}(x ² + x + 1)]

Ahora pon x = 1, obtenemos

= 4/{(3)(√1 + √1)}

= 4/6

= 2/3

Pregunta 19. Lim _x→2 {√(1 + 4x) – √(5 + 2x)}/(x – 2)

Solución:

Tenemos, Lim _x→2 {√(1 + 4x) – √(5 + 2x)}/(x – 2)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 2, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→2}\frac{\sqrt{(1 + 4x)} - \sqrt{(5 + 2x)}}{(x - 2)} \times \frac{\sqrt{(1 + 4x)} + \sqrt{(5 + 2x)}}{\sqrt{(1 + 4x)} + \sqrt{(5 + 2x)}}$

= Lim _x→2 {√(1 + 4x) – √(5+2x)}/[(x – 2){√(1 + 4x) + √(5 + 2x)}]

= Lim _x→2 {(1 + 4x) – (5 + 2x)}/[(x – 2){√(1 + 4x) + √(5 + 2x)}]

= Lim _x→2 {2(x – 2)}/[(x – 2){√(1 + 4x) + √(5 + 2x)}]

= Lim _x→2 (2)/{√(1 + 4x) + √(5 + 2x)}

Ahora pon x = 2, obtenemos

= 2/{√(1 + 8) + √(5 + 4)}

= 2/(3 + 3)

= 1/3

Pregunta 20. Lim _x→1 {√(3 + x) – √(5 – x)}/(x ² – 1)

Solución:

Tenemos, Lim _x→1 {√(3 + x) – √(5 – x)}/(x ² – 1)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 1, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→1}\frac{\sqrt{(3 + x)} - \sqrt{(5 - x)}}{(x^2 - 1)} \times \frac{\sqrt{(3 + x)} + \sqrt{(5 - x)}}{\sqrt{(3 + x)} + \sqrt{(5 - x)}}$

= Lim _x→1 {(3 + x) – (5 – x)}/[(x ² – 1){√(3 + x) + √(5 – x)}]

= Lim _x→1 {2(x – 1)}/[(x – 1)(x + 1){√(3 + x) + √(5 – x)}]

= Lim _x→1 (2)/[(x + 1){√(3 + x) + √(5 – x)}]

Ahora pon x = 1, obtenemos

= 2/{2(2 + 2)}

= 1/4

Pregunta 21. Lim _x→0 {√(1 + x ² ) – √(1 – x ² )}/(x)

Solución:

Tenemos, Lim _x→0 {√(1 + x ² ) – √(1 – x ² )}/(x)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{\sqrt{(1 + x^2)} - \sqrt{(1 - x^2)}}{x} \times \frac{\sqrt{(1 + x^2)} + \sqrt{(1 - x^2)}}{\sqrt{(1 + x^2)} + \sqrt{(1 - x^2)}}$

= Lim _x→0 {(1 + x ² ) – (1 – x ² )}/[x{√(1 + x ² ) + √(1 – x ² )}]

= Lim _x→0 {(1 + x ² ) – (1 – x ² )}/[x{√(1 + x ² ) + √(1 – x ² )}]

= Lim _x→0 (2x ² /[x{√(1 + x ² ) + √(1 – x ² )}]

= Lim _x→0 (2x/{√(1 + x ² ) + √(1 – x ² )}

Ahora pon x = 0, obtenemos

= 2 × 0/(√1 + √1)

= 0

Pregunta 22. Lim _x→0 {√(1 + x + x ² ) – √(x + 1)}/(2x ² )

Solución:

Tenemos, Lim _x→0 {√(1 + x + x ² ) – √(x + 1)}/(2x ² )

Encuentre el límite de la ecuación dada

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{\sqrt{(1 + x + x^2)} - \sqrt{(x + 1)}}{2x^2} \times \frac{\sqrt{(1 + x + x^2)} + \sqrt{(x + 1)}}{\sqrt{(1 + x + x^2)} + \sqrt{(x + 1)}}$

= Lim _x→0 {(1 + x + x ² ) – (x + 1)}/[2x ² {√(1 + x + x ² ) – √(x + 1)}]

= Lim _x→0 (x ² )/[2x ² {√(1 + x + x ² ) – √(x + 1)}]

= Lim _x→0 (1)/[2{√(1 + x + x ² ) – √(x + 1)}]

Ahora pon x = 0, obtenemos

= 1/{2(√1 + √1)

= 1/4

Pregunta 23. Lim _x→4 {2 – √x}/(4 – x)

Solución:

Tenemos, Lim _x→4 {2 – √x}/(4 – x)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 4, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→4}\frac{2 - √x}{(4 - x)} \times \frac{2 + √x}{2 + √x}$

= Lim _x→4 {4 – x}/[(4 – x){2 + √x}]

= Lim _x→4 {4 – x}/[(4 – x){2 + √x}]

= Lim _x→4 (1)/{2 + √x}

Ahora pon x = 4, obtenemos

= 1/(2 + 2)

= 1/4

Pregunta 24. Lim _x→a (x – a)/{√x – √a}

Solución:

Tenemos, Lim _x→a (x – a)/{√x – √a}

Encuentre el límite de la ecuación dada

Cuando ponemos x = a, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→a}\frac{(x - a)}{√x - √a} \times \frac{√x + √a}{√x + √a}$

= Lim _x→a [(x – a){√x – √a}]/(x – a)

= Lim _x→a {√x + √a}

Ahora pon x = a, obtenemos

= √a + √a

= 2√a

Pregunta 25. Lim _x→0 {√(1 + 3x) – √(1 – 3x)}/(x)

Solución:

Tenemos, Lim _x→0 {√(1 + 3x) – √(1 – 3x)}/(x)

Encuentre el límite de la ecuación dada

Cuando ponemos x = a, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{\sqrt{(1 + 3x)} - \sqrt{(1 - 3x)}}{x} \times \frac{\sqrt{(1 + 3x)} + \sqrt{(1 - 3x)}}{\sqrt{(1 + 3x)} + \sqrt{(1 - 3x)}}$

= Lim _x→0 {(1 + 3x) – (1 – 3x)}/[(x){√(1 + 3x) – √(1 – 3x)}]

= Lim _x→0 (6x)/[(x){√(1 + 3x) – √(1 – 3x)}]

= Lim _x→0 (6)/{√(1 + 3x) – √(1 – 3x)}

Ahora pon x = 0, obtenemos

= 6/(√1 + √1)

= 6/2

= 3

Pregunta 26. Lim _x→0 {√(2 – x) – √(2 + x)}/(x)

Solución:

Tenemos, Lim _x→0 {√(2 – x) – √(2 + x)}/(x)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→0}\frac{\sqrt{(2 - x)} - \sqrt{(2 + x)}}{x} \times \frac{\sqrt{(2 - x)} + \sqrt{(2 + x)}}{\sqrt{(2 - x)} + \sqrt{(2 + x)}}$

= Lim _x→0 {(2 – x) – (2 + x)}/[x{√(2 – x) + √(2 + x)}]

= Lim _x→0 (-2x)/[x{√(2 – x) + √(2 + x)}]

= Lim _x→0 (-2)/{√(2 – x) + √(2 + x)}

Ahora pon x = 0, obtenemos

= (-2)/(√2 + √2)

= (-2)/(2√2)

= -1/(√2)

Pregunta 27. Lim _x→1 {√(3 + x) – √(5 – x)}/(x ² – 1)

Solución:

Tenemos, Lim _x→1 {√(3 + x) – √(5 – x)}/(x ² – 1)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 1, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{x→1}\frac{\sqrt{(3 + x)} - \sqrt{(5 - x)}}{(x^2 - 1)} \times \frac{\sqrt{(3 + x)} + \sqrt{(5 - x)}}{\sqrt{(3 + x)} + \sqrt{(5 - x)}}$

= Lim _x→1 {(3 + x) – (5 – x)}/[(x ² – 1){√(3 + x) + √(5 – x)}]

= Lim _x→1 {2(x – 1)}/[(x – 1)(x + 1){√(3 + x) + √(5 – x)}]

= Lim _x→1 (2)/[(x + 1){√(3 + x) + √(5 – x)}]

Ahora pon x = 1, obtenemos

= 2/{(2)(√4 + √4)}

= 2/8

= 1/4

Pregunta 28. Lim _x→1 {(2x – 3)(√x – 1)}/(3x ² + 3x – 6)

Solución:

Tenemos, Lim _x→1 {(2x – 3)(√x – 1)}/(3x ² + 3x – 6)

Encuentre el límite de la ecuación dada

Cuando ponemos x = 1, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= Lim _x→1 {(2x – 3)(x – 1)}/[(3x ² + 3x – 6)(√x + 1)]

= Lim _x→1 {(2x – 3)(x – 1)}/[3(x ² + x – 2)(√x + 1)]

= Lim _x→1 {(2x – 3)(x – 1)}/[3(x – 1)(x + 2)(√x + 1)]

= Lim _x→1 (2x – 3)/[3(x + 2)(√x + 1)]

Ahora pon x = 1, obtenemos

= (2 – 3)/{3(3)(√1 + 1)

= -1/(3 × 3 × 2)

= -1/18

Pregunta 29. Lim _x→0 {√(1 + x ² ) – √(1 + x)}/{√(1 + x ³ ) – √(1 + x)}

Solución:

Tenemos, Lim _x→0 {√(1 + x ² ) – √(1 + x)}/{√(1 + x ³ ) – √(1 + x)}

Encuentre el límite de la ecuación dada

Cuando ponemos x = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

$=\lim_{x\to0}\frac{(\sqrt{1+x^2}-\sqrt{1+x})(\sqrt{1+x^2}+\sqrt{1+x})}{(\sqrt{1+x^3}-\sqrt{1+x})(\sqrt{1+x^3}+\sqrt{1+x})}$

$=\lim_{x\to0}\frac{x(x-1)}{x(x^2-1)}×\frac{(\sqrt{1+x^3}+\sqrt{x+1})}{(\sqrt{1+x^2}+\sqrt{x+1})}$

$=\lim_{x\to0}\frac{[(1+x^2)-(1+x)]}{[(1+x^3)-(1+x)}×\frac{(\sqrt{1+x^3}+\sqrt{x+1})}{(\sqrt{1+x^2}+\sqrt{x+1})}$

$=\lim_{x\to0}\frac{(x^2-x)}{(x^3-x)}×\frac{(\sqrt{1+x^3}+\sqrt{x+1})}{(\sqrt{1+x^2}+\sqrt{x+1})}$

$=\lim_{x\to0}\frac{1}{(x+1)}×\frac{(\sqrt{1+x^3}+\sqrt{x+1})}{(\sqrt{1+x^2}+\sqrt{x+1})}$

Ahora pon x = 0, obtenemos

= (√1 + √1)/{1(√1 + √1)}

= 2/2

= 1

Pregunta 30. Lim _x→1 {x ² – √x}/{√x – 1}

Solución:

Tenemos, Lim _x→1 {x ² – √x}/{√x – 1}

Encuentre el límite de la ecuación dada

Cuando ponemos x = 1, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= Lim _x→1 {√x(x√x -1)}/{√x – 1}

= Lim _x→1 {√x(x ^3/2 – 1)}/{√x – 1}

= Lim _x→1 [√x{(√x) ³ – 1}]/{√x – 1}

= Lim _x→1 [(√x)(√x – 1)(x + √x + 1)]/{√x – 1}

= Límite _x→1 [(√x)(x + √x + 1)]

Ahora pon x = 1, obtenemos

= (√1)(1 + √1 + 1)

= 3

Pregunta 31. Lim _h→0 {√(x + h) – √x}/(h), x ≠ 0

Solución:

Tenemos, Lim _h→0 {√(x + h) – √x}/(h)

Encuentre el límite de la ecuación dada

Cuando ponemos h = 0, esta expresión toma la forma de 0/0.

Entonces, al racionalizar la ecuación dada obtenemos

= $Lim_{h→0}\frac{\sqrt{(x + h)} - \sqrt{x}}{h} \times \frac{\sqrt{(x + h)} + \sqrt{x}}{\sqrt{(x + h)} + \sqrt{x}}$

= Lim _h→0 {(x + h) – x}/[h{√(x + h) + √x}]

= Lím _h→0( h)/[h{√(x + h) + √x}]

= Lím _h→0 (1)/{√(x + h) + √x}

Ahora pon x = 0, obtenemos

= 1/(√x + √x)

= 1/(2√x)

Pregunta 32. Lim _x→√10 {√(7 + 2x) – (√5 + √2)}/(x ² – 10)

Solución:

Tenemos, Lim _x→√10 {√(7 + 2x) – (√5 + √2)}/(x ² – 10)

= Lim _x→√10 {√(7 + 2x) – √(√5 + √2) ² }/{(x – √10)(x + √10)}

= Lim _x→√10 {√(7 + 2x) – √(5 + 2 + 2√5√2)}/{(x – √10)(x + √10)}

= Lim _x→√10 {√(7 + 2x) – √(7 + 2√10)}/{(x – √10)(x + √10)}

Sobre la racionalización del numerador.

= $\lim_{x\to\sqrt{10}}\frac{(\sqrt{7+2x}-\sqrt{7+2\sqrt{10}})(\sqrt{7+2x}+\sqrt{7+2\sqrt{10}})}{(x-\sqrt{10})(x+\sqrt{10})(\sqrt{7+2x}+\sqrt{7+2\sqrt{10}})}$

= $\lim_{x\to\sqrt{10}}\frac{(7+2x)-(7+2\sqrt{10})}{(x-\sqrt{10})(x+\sqrt{10})(\sqrt{7+2x}+\sqrt{7+2\sqrt{10}})}$

= $\lim_{x\to\sqrt{10}}\frac{2(x-\sqrt{10})}{(x-\sqrt{10})(x+\sqrt{10})(\sqrt{7+2x}+\sqrt{7+2\sqrt{10}})}$

Ahora pon x = √10, obtenemos

= $\frac{2}{(\sqrt{10}+\sqrt{10})(2\sqrt{7+2\sqrt{10}}}$

= $\frac{1}{(2\sqrt{10})(\sqrt{7+2\sqrt{10}}}$

= $\frac{1}{(2\sqrt{10})(\sqrt{\sqrt{5}+\sqrt{2})^2}}$

= 1/{(2√10)(√5 + √2)}

Sobre la racionalización del denominador.

= (√5 – √2)/{(2√10)(5 – 2)}

= (√5 – √2)/(6√10)

Pregunta 33. Lim _x→√6 {√(5 + 2x) – (√3 + √2)}/(x ² – 6)

Solución:

Tenemos, Lim _x→√6 {√(5 + 2x) – (√3 + √2)}/(x ² – 6)

= Lim _x→√6 {√(5 + 2x) – √(√3 + √2) ² }/{(x – √6)(x + √6)}

= Lim _x→√6 {√(5 + 2x) – √(3 + 2 + 2√3√2)}/{(x – √6)(x + √6)}

= Lim _x→√6 {√(5 + 2x) – √(5 + 2√6)}/{(x -√6)(x + √6)}

Sobre la racionalización del numerador.

= $\lim_{x\to\sqrt{6}}\frac{(\sqrt{5+2x}-\sqrt{5+2\sqrt{6}})(\sqrt{5+2x}+\sqrt{5+2\sqrt{6}})}{(x-\sqrt{6})(x+\sqrt{6})(\sqrt{5+2x}+\sqrt{5+2\sqrt{6}})}$

= $\lim_{x\to\sqrt{6}}\frac{(5+2x)-(5+2\sqrt{6})}{(x-\sqrt{6})(x+\sqrt{6})(\sqrt{5+2x}+\sqrt{5+2\sqrt{6}})}$

= $\lim_{x\to\sqrt{6}}\frac{2(x-\sqrt{6})}{(x-\sqrt{6})(x+\sqrt{6})(\sqrt{5+2x}+\sqrt{5+2\sqrt{6}})}$

= $\lim_{x\to\sqrt{6}}\frac2{(x+\sqrt{6})(\sqrt{5+2x}+\sqrt{5+2\sqrt{6}})}$

Ahora pon x = √6, obtenemos

= $\frac2{(\sqrt6+\sqrt{6})(\sqrt{5+2\sqrt{5}}+\sqrt{5+2\sqrt{6}})}$

= $\frac2{(2\sqrt{6})(2\sqrt{5+2\sqrt{5}})}$

= $\frac1{(2\sqrt{6})(\sqrt{5+2\sqrt{5}})}$

= 1/{(2√6)(√3 + √2)}

Al racionalizar el denominador, obtenemos

= (√3 – √2)/{(2√6)(3 – 2)}

= (√3 – √2)/(2√6)

Pregunta 34. Lim _x→√2 {√(3 + 2x) – (√2 + 1)}/(x ² – 2)

Solución:

Tenemos, Lim _x→√2 {√(3 + 2x) – (√2 + 1)}/(x ² – 2)

= Lim _x→√2 {√(3 + 2x) – √(√2 + 1) ² }/{(x – √2)(x + √2)}

= Lim _x→√2 {√(3 + 2x) – √(2 + 1 + 2√3)}/{(x – √2)(x + √2)}

= Lim _x→√2 {√(3 + 2x) – √(3 + 2√3)}/{(x – √2)(x + √2)}

Sobre la racionalización del numerador.

= $\lim_{x\to\sqrt{2}}\frac{(\sqrt{3+2x}-\sqrt{3+2\sqrt{2}})(\sqrt{3+2x}+\sqrt{3+2\sqrt{2}})}{(x-\sqrt{2})(x+\sqrt{2})(\sqrt{3+2x}+\sqrt{3+2\sqrt{2}})}$

= $\lim_{x\to\sqrt{2}}\frac{(3+2x)-(3+2\sqrt2)}{(x-\sqrt{2})(x+\sqrt{2})(\sqrt{3+2x}+\sqrt{3+2\sqrt2})}$

= $\lim_{x\to\sqrt{2}}\frac{(3+2x)-(3+2\sqrt2)}{(x-\sqrt{2})(x+\sqrt{2})(\sqrt{3+2x}+\sqrt{3+2\sqrt2})}$

= $\lim_{x\to\sqrt{2}}\frac{2(x-\sqrt{3})}{(x-\sqrt{2})(x+\sqrt{2})(\sqrt{3+2x}+\sqrt{3+2\sqrt2})}$

= $\lim_{x\to\sqrt{2}}\frac{2}{(x+\sqrt{2})(\sqrt{3+2x}+\sqrt{3+2\sqrt2})}$

Ahora pon x = √2, obtenemos

= $\frac2{(\sqrt2+\sqrt2)(\sqrt{3+2\sqrt{5}}+\sqrt{3+2\sqrt2})}$

= $\frac2{(2\sqrt2)(2\sqrt{3+2\sqrt2})}$

= $\frac1{(2\sqrt{2})(\sqrt{3+2\sqrt2})}$

= 1/{(2√2)(√2 + 1)}

Al racionalizar el denominador, obtenemos

= (√2 – 1)/{(2√2)(2 – 1)}

= (√2 – 1)/(2√2)

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 RD Sharma Solutions – Capítulo 29 Límites – Ejercicio 29.4 | conjunto 2

Evalúa los siguientes límites:

Pregunta 18. Lim _x→1 {√(5x – 4) – √x}/(x ³ – 1)

Pregunta 19. Lim _x→2 {√(1 + 4x) – √(5 + 2x)}/(x – 2)

Pregunta 20. Lim _x→1 {√(3 + x) – √(5 – x)}/(x ² – 1)

Pregunta 21. Lim _x→0 {√(1 + x ² ) – √(1 – x ² )}/(x)

Pregunta 22. Lim _x→0 {√(1 + x + x ² ) – √(x + 1)}/(2x ² )

Pregunta 23. Lim _x→4 {2 – √x}/(4 – x)

Pregunta 24. Lim _x→a (x – a)/{√x – √a}

Pregunta 25. Lim _x→0 {√(1 + 3x) – √(1 – 3x)}/(x)

Pregunta 26. Lim _x→0 {√(2 – x) – √(2 + x)}/(x)

Pregunta 27. Lim _x→1 {√(3 + x) – √(5 – x)}/(x ² – 1)

Pregunta 28. Lim _x→1 {(2x – 3)(√x – 1)}/(3x ² + 3x – 6)

Pregunta 29. Lim _x→0 {√(1 + x ² ) – √(1 + x)}/{√(1 + x ³ ) – √(1 + x)}

Pregunta 30. Lim _x→1 {x ² – √x}/{√x – 1}

Pregunta 31. Lim _h→0 {√(x + h) – √x}/(h), x ≠ 0

Pregunta 32. Lim _x→√10 {√(7 + 2x) – (√5 + √2)}/(x ² – 10)

Pregunta 33. Lim _x→√6 {√(5 + 2x) – (√3 + √2)}/(x ² – 6)

Pregunta 34. Lim _x→√2 {√(3 + 2x) – (√2 + 1)}/(x ² – 2)

Deja una respuesta Cancelar la respuesta

Evalúa los siguientes límites:

Pregunta 18. Lim x→1 {√(5x – 4) – √x}/(x 3 – 1)

Pregunta 19. Lim x→2 {√(1 + 4x) – √(5 + 2x)}/(x – 2)

Pregunta 20. Lim x→1 {√(3 + x) – √(5 – x)}/(x 2 – 1)

Pregunta 21. Lim x→0 {√(1 + x 2 ) – √(1 – x 2 )}/(x)

Pregunta 22. Lim x→0 {√(1 + x + x 2 ) – √(x + 1)}/(2x 2 )

Pregunta 23. Lim x→4 {2 – √x}/(4 – x)

Pregunta 24. Lim x→a (x – a)/{√x – √a}

Pregunta 25. Lim x→0 {√(1 + 3x) – √(1 – 3x)}/(x)

Pregunta 26. Lim x→0 {√(2 – x) – √(2 + x)}/(x)

Pregunta 27. Lim x→1 {√(3 + x) – √(5 – x)}/(x 2 – 1)

Pregunta 28. Lim x→1 {(2x – 3)(√x – 1)}/(3x 2 + 3x – 6)

Pregunta 29. Lim x→0 {√(1 + x 2 ) – √(1 + x)}/{√(1 + x 3 ) – √(1 + x)}

Pregunta 30. Lim x→1 {x 2 – √x}/{√x – 1}

Pregunta 31. Lim h→0 {√(x + h) – √x}/(h), x ≠ 0

Pregunta 32. Lim x→√10 {√(7 + 2x) – (√5 + √2)}/(x 2 – 10)

Pregunta 33. Lim x→√6 {√(5 + 2x) – (√3 + √2)}/(x 2 – 6)

Pregunta 34. Lim x→√2 {√(3 + 2x) – (√2 + 1)}/(x 2 – 2)

Deja una respuesta Cancelar la respuesta

Pregunta 18. Lim _x→1 {√(5x – 4) – √x}/(x ³ – 1)

Pregunta 19. Lim _x→2 {√(1 + 4x) – √(5 + 2x)}/(x – 2)

Pregunta 20. Lim _x→1 {√(3 + x) – √(5 – x)}/(x ² – 1)

Pregunta 21. Lim _x→0 {√(1 + x ² ) – √(1 – x ² )}/(x)

Pregunta 22. Lim _x→0 {√(1 + x + x ² ) – √(x + 1)}/(2x ² )

Pregunta 23. Lim _x→4 {2 – √x}/(4 – x)

Pregunta 24. Lim _x→a (x – a)/{√x – √a}

Pregunta 25. Lim _x→0 {√(1 + 3x) – √(1 – 3x)}/(x)

Pregunta 26. Lim _x→0 {√(2 – x) – √(2 + x)}/(x)

Pregunta 27. Lim _x→1 {√(3 + x) – √(5 – x)}/(x ² – 1)

Pregunta 28. Lim _x→1 {(2x – 3)(√x – 1)}/(3x ² + 3x – 6)

Pregunta 29. Lim _x→0 {√(1 + x ² ) – √(1 + x)}/{√(1 + x ³ ) – √(1 + x)}

Pregunta 30. Lim _x→1 {x ² – √x}/{√x – 1}

Pregunta 31. Lim _h→0 {√(x + h) – √x}/(h), x ≠ 0

Pregunta 32. Lim _x→√10 {√(7 + 2x) – (√5 + √2)}/(x ² – 10)

Pregunta 33. Lim _x→√6 {√(5 + 2x) – (√3 + √2)}/(x ² – 6)

Pregunta 34. Lim _x→√2 {√(3 + 2x) – (√2 + 1)}/(x ² – 2)