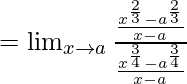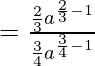Pregunta 11. 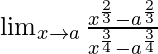
Solución:
Dividiendo numerador y denominador por xa
Aplicando la fórmula
aquí,
para el numerador y
para el denominador
Pregunta 12. Si 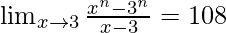 , encuentra el valor de n.
, encuentra el valor de n.
Solución:
IZQ =
Aplicando la fórmula
IZQ =
lado derecho = 108
LHS = RHS
Pregunta 13. Si 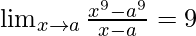 , encuentra todos los valores posibles de a.
, encuentra todos los valores posibles de a.
Solución:
IZQ=
Aplicando la fórmula
IZQ =
lado derecho = 9
LHS = RHS
a=1 y a=-1
Pregunta 14. Si 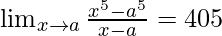 , encuentra todos los valores posibles de a.
, encuentra todos los valores posibles de a.
Solución:
IZQ =
Aplicando la fórmula
IZQ =
lado derecho = 405
LHS = RHS
a=3 y a=-3
Pregunta 15. Si  , encuentra todos los valores posibles de a.
, encuentra todos los valores posibles de a.
Solución:
IZQ=
Aplicando la fórmula
IZQ=
RHS=
IZQ=DERECHA
a=1 y a=-1
Pregunta 16. Si 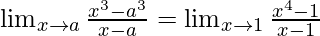 , encuentra todos los valores posibles de a.
, encuentra todos los valores posibles de a.
Solución:
IZQ=
Aplicando la fórmula
IZQ=
RHS=
IZQ=DERECHA
y
Publicación traducida automáticamente
Artículo escrito por manandeep1610 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA