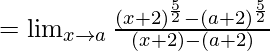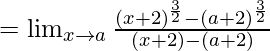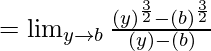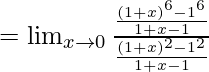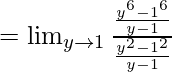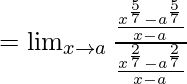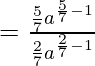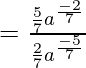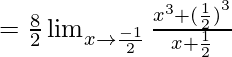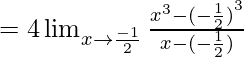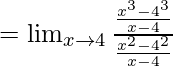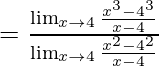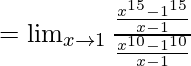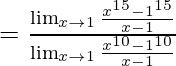Clase 11 RD Sharma Solutions – Capítulo 29 Límites – Ejercicio 29.5 | Serie 1

Posted on by Rudeus Greyrat

Evalúa los siguientes límites:

Pregunta 1. 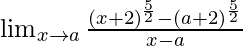\lim_{x \to a} \frac {(x+2)^{\frac 5 2}-(a+2)^{\frac 5 2}} {x-a}

Solución:

\lim_{x \to a} \frac {(x+2)^{\frac 5 2}-(a+2)^{\frac 5 2}} {x-a}

=\lim_{x \to a} \frac {(x+2)^{\frac 5 2}-(a+2)^{\frac 5 2}} {(x+2)-(a+2)}

Sean y = x + 2 y b = a + 2

=\lim_{y \to b} \frac {(y)^{\frac 5 2}-(b)^{\frac 5 2}} {(y)-(b)} 

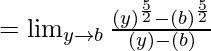
=\frac 5 2 b^{{\frac 5 2} -1}  [usando la fórmula  \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1}]

=\frac 5 2 (a+2)^{{\frac 5 2} -1}

=\frac 5 2 (a+2)^{\frac 3 2}

Pregunta 2. 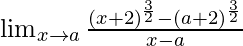\lim_{x \to a} \frac {(x+2)^{\frac 3 2}-(a+2)^{\frac 3 2}} {x-a}

Solución:

\lim_{x \to a} \frac {(x+2)^{\frac 3 2}-(a+2)^{\frac 3 2}} {x-a}

=\lim_{x \to a} \frac {(x+2)^{\frac 3 2}-(a+2)^{\frac 3 2}} {(x+2)-(a+2)}

Sean y=x+2 y b=a+2

=\lim_{y \to b} \frac {(y)^{\frac 3 2}-(b)^{\frac 3 2}} {(y)-(b)}

=\frac 3 2 b^{{\frac 3 2} -1}  [usando la fórmula  \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1}]

=\frac 3 2 (a+2)^{{\frac 3 2} -1}

=\frac 3 2 (a+2)^{\frac 1 2}

Pregunta 3. 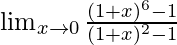\lim_{x \to 0} \frac {(1+x)^{6}-1} {(1+x)^2-1}

Solución:

\lim_{x \to 0} \frac {(1+x)^{6}-1} {(1+x)^2-1}

Dividiendo el numerador y denominador con 1+x-1

=\lim_{x \to 0} \frac {\frac {(1+x)^{6}-1^6} {1+x-1} } {\frac {(1+x)^{2}-1^2} {1+x-1}}

Sea y=1+x como x \to 0,y\to 1

=\lim_{y \to 1} \frac {\frac {y^{6}-1^6} {y-1} } {\frac {y^{2}-1^2} {y-1}}

=\frac {6(1)^{6-1}} {2(1)^{2-1}}  [usando la fórmula  \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1}]

=\frac 6 2

=3

Pregunta 4. 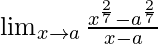\lim_{x \to a} \frac {x^{\frac 2 7}-a^{\frac 2 7}} {x-a}

Solución:

\lim_{x \to a} \frac {x^{\frac 2 7}-a^{\frac 2 7}} {x-a}

Aplicando la fórmula  \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1}, aquí, n=\frac 2 7

=\frac 2 7a^{{\frac 2 7}-1}

=\frac 2 7 a^{\frac {-5} {7}}

Pregunta 5. 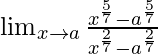\lim_{x \to a} \frac {x^{\frac 5 7}-a^{\frac 5 7}} {x^{\frac 2 7}-a^{\frac 2 7}}

Solución:

\lim_{x \to a} \frac {x^{\frac 5 7}-a^{\frac 5 7}} {x^{\frac 2 7}-a^{\frac 2 7}}

Dividiendo el numerador y el denominador con xa

=\lim_{x \to a} \frac { \frac {x^{\frac 5 7}-a^{\frac 5 7}} {x-a}} {\frac {x^{\frac 2 7}-a^{\frac 2 7}} {x-a}}

Aplicando la fórmula  \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1}, aquí,  n=\frac 5 7  en numerador y  n=\frac 2 7  en denominador 

=\frac {\frac 5 7a^{{\frac 5 7}-1}} {\frac 2 7a^{{\frac 2 7}-1}}

=\frac {\frac 5 7a^{\frac {-2} 7}} {\frac 2 7a^{\frac {-5} 7}}

=\frac 5 2a^{\frac {-2} {7} + \frac {5} {7}}

=\frac 5 2a^{\frac {3} {7}}

Pregunta 6. 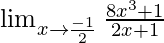\lim_{x \to {\frac {-1} 2}} \frac {8x^3+1} {2x+1}

Solución:

\lim_{x \to {\frac {-1} 2}} \frac {8x^3+1} {2x+1}

=\frac 8 2\lim_{x \to {\frac {-1} 2}} \frac {x^3+{(\frac 1 2)}^3} {x+\frac 1 2}

=4\lim_{x \to {\frac {-1} 2}} \frac {x^3-{(-\frac 1 2)}^3} {x-(-\frac 1 2)}

Aplicando la fórmula  \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1} aquí,  n=3 y a=\frac {-1} {2}

=4 \times 3(\frac {-1} 2)^{3-1}

=4 \times 3 \times \frac 1 4

=3

Pregunta 7. 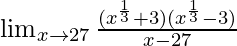\lim_{x \to 27} \frac {({x^{\frac 1 3}+3})({x^{\frac 1 3}-3})} {x-27}

Solución:

\lim_{x \to 27} \frac {({x^{\frac 1 3}+3})({x^{\frac 1 3}-3})} {x-27}

=\lim_{x \to 27} \frac {({x^{\frac 2 3}-9})} {x-27}

=\lim_{x \to 27} \frac {({x^{\frac 2 3}-27^{\frac 2 3}})} {x-27}

Aplicando la fórmula \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1}

=\frac 2 3(27)^{\frac 2 3 -1}

=\frac 2 3(27)^{\frac {-1} 3}

=\frac 2 3\times \frac 1 {(27)^{\frac 1 3}}

=\frac 2 3\times \frac 1 3

=\frac 2 9

pregunta 8 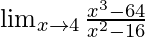\lim_{x \to 4} \frac {{x^3-64}} {x^2-16}

Solución: 

\lim_{x \to 4} \frac {{x^3-64}} {x^2-16}

=\lim_{x \to 4} \frac {{x^3-4^3}} {x^2-4^2}

Dividiendo el numerador y el denominador con x-4

=\lim_{x \to 4} \frac {\frac {x^3-4^3} {x-4}} {\frac {x^2-4^2} {x-4}}

= \frac {\lim_{x \to 4}{\frac {x^3-4^3} {x-4}}} {\lim_{x \to 4}{\frac {x^2-4^2} {x-4}}}

Aplicando la fórmula  \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1}aquí, n=3 en el numerador y n=2 en el denominador 

= \frac {3(4)^{3-1}} {2(4)^{2-1}}

= \frac {3(4)^{2}} {2(4)}

=6

Pregunta 9. 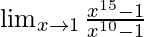\lim_{x \to 1} \frac {{x^{15}-1}} {x^{10}-1}

Solución

\lim_{x \to 1} \frac {{x^{15}-1}} {x^{10}-1}

Dividiendo el numerador y el denominador con x-1

=\lim_{x \to 1} \frac {\frac {x^{15}-1^{15}} {x-1}} {\frac {x^{10}-1^{10}} {x-1}}

= \frac {\lim_{x \to 1}\frac {x^{15}-1^{15}} {x-1}} {\lim_{x \to 1}\frac {x^{10}-1^{10}} {x-1}}

Aplicando la fórmula  \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1}aquí, 

n=15 en numerador y n=10 en denominador

=\frac {15(1)^{15-1}}{10(1)^{10-1}}

=\frac {15} {10}

= \frac 3 2

Pregunta 10. 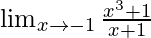\lim_{x \to {-1}} \frac {{x^{3}+1}} {x+1}

Solución:

\lim_{x \to {-1}} \frac {{x^{3}+1}} {x+1}

=\lim_{x \to {-1}} \frac {{x^{3}-(-1)^3}} {x-(-1)}

Aplicando la fórmula \lim_{x \to a} \frac {x^{n}-a^{n}} {x-a}=na^{n-1}

=3(-1)^{3-1}

=3(-1)^2

=3

Publicación traducida automáticamente

Artículo escrito por manandeep1610 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *