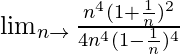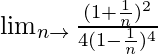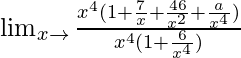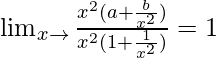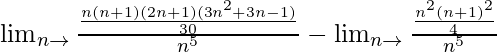Clase 11 RD Sharma Solutions – Capítulo 29 Límites – Ejercicio 29.6

Pregunta 14. Lim _n→∞ {1 ² + 2 ² + ……………. + n ² }/(n ³ )

Solución:

Tenemos,

Lim _n→∞ {1 ² + 2 ² + ……………. + n ² }/(n ³ )

= Lím _n→∞ [n(n+1)(2n+1)]/6n ³

= Lím _n→∞ [(n+1)(2n+1)]/6n ²

= $\lim_{n\to∞}\frac{(n+1)}{n}\frac{2n+1}{n}\frac{1}{6}$

$\lim_{n\to∞}(1+\frac{1}{n})(2+\frac{1}{n})\frac{1}{6}$

Cuando n → ∞, (1/n) → 0

= 2/6

= 1/3

Pregunta 15. Lim _n→∞ {1 + 2 + 3 + 4 +………………. + n – 1}/n ²

Solución:

Tenemos,

Lim _n→∞ {1 + 2 + 3 + 4 +………………. + n – 1}/n ²

= Lím _n→∞ [n(n – 1)/2n ² ]

= Lím _n→∞ [n ² – n/2n ² ]

= Lím _n→∞ (1/2 – 1/2n)

Cuando n → ∞, (1/n) → 0

= 1/2

Pregunta 16. Lim _n→∞ {1 ³ + 2 ³ + ……………. + n ³ }/(n ⁴ )

Solución:

Tenemos,

Lim _n→∞ {1 ³ + 2 ³ + ……………. + n ³ }/(n ⁴ )

= Lim _n→∞ [n ² (n + 1) ² ]/(4n ⁴ ) [puesto que (1 ³ + 2 ³ + …………. + n ³ ) = n ² (n + 1) ² /4]

= Lim _n→∞ [(n + 1) ² ]/(4n ² )

= Lim _n→∞ [(1 + 1/n) ² × (1/4)]

Cuando n → ∞, (1/n) → 0

= 1/4

Pregunta 17. Lim _n→∞ {1 ³ + 2 ³ + ……………. + n ³ }/(n – 1) ⁴

Solución:

Tenemos,

Lim _n→∞ {1 ³ + 2 ³ + ……………. + n ³ }/(n – 1) ⁴

= Lim _n→∞ [n ² (n + 1) ² ]/[4(n – 1) ⁴ ] [ya que (1 ³ + 2 ³ + …………. + n ³ ) = n ² (n + 1 ) ² /4]

= $\lim_{n\to∞}\frac{n^4(1+\frac{1}{n})^2}{4n^4(1-\frac{1}{n})^4}$

= $\lim_{n\to∞}\frac{(1+\frac{1}{n})^2}{4(1-\frac{1}{n})^4}$

Cuando n → ∞, (1/n) → 0

= 1/4

Pregunta 18. Lim _x→∞ [√x{√(x + 1) – √x}]

Solución:

Tenemos,

Lim _x→∞ [√x{√(x + 1) – √x}]

Al racionalizar el numerador, obtenemos

= Lim _x→∞ [(√x){(x + 1) – x}]/{√(x + 1) + √x}

= Lim _x→∞ (√x}/{√(x + 1) + √x}

= $\lim_{x\to∞}\frac{\sqrt{x}}{\sqrt{x}(1+\frac{1}{x}+1)}$

Cuando x → ∞, (1/x) → 0.

= 1/(√1 + 1)

= 1/2

Pregunta 19. Lim _x→∞ [1/3 + 1/3 ² + 1/3 ³ + ……………… + 1/3 ⁿ ]

Solución:

Tenemos,

Lim _x→∞ [1/3 + 1/3 ² + 1/3 ³ + ……………… + 1/3 ⁿ ]

Esta es la serie GP de relación común 1/3.

Entonces, la suma de n términos de GP S _n = [a(1 – r ⁿ )]/(1 – r) (i)

a = 1/3, r = 1/3

Al poner el valor de a & r en la ecuación (i), obtenemos

Sn = (1/2)(1 – 1 _/³ⁿ )

= Lim _x→∞ [(1/2)(1 – 1/3 ⁿ )]

= (1/2)Lím _x→∞ (1 – 1/3 ⁿ )

= (1/2)(1 – 0)

= 1/2

Pregunta 20. Lim _x→∞ {(x ⁴ + 7x ³ + 46x + a)}/{(x ⁴ + 6)}.

Solución:

Tenemos,

Lim _x→∞ {(x ⁴ + 7x ³ + 46x + a)}/{(x ⁴ + 6)}

= $\lim_{x\to∞}\frac{x^4(1+\frac{7}{x}+\frac{46}{x^2}+\frac{a}{x^4})}{x^4(1+\frac{6}{x^4})}$

Cuando x → ∞, (1/x), (1/x ² ), (1/x ³ ), (1/x ⁴ ) → 0

= 1/1

= 1

Pregunta 21. f(x) = (ax ² + b)/(x ² + 1), Lim _x→0 f(x) = 1, Lim _x→∞ f(x) = 1, luego prueba que f(- 2) = f(2) = 1

Solución:

Tenemos,

f(x) = (ax ² + b)/(x ² + 1)

= Lim _x→0 [(ax ² + b)/(x ² + 1)]

b/1 = 1

segundo = 1

= Lim _x→∞ [(ax ² + b)/(x ² + 1)]

= $\lim_{x\to∞}\frac{x^2(a+\frac{b}{x^2})}{x^2(1+\frac{1}{x^2})}=1$

Cuando x → ∞, (1/x ² ) → 0.

(a + 0)/(1 + 0) = 1

un = 1

Por lo tanto, a = 1, b = 1

f(x) = (x2 ⁺ 1)/(x2 ⁺ 1)

f(x) = 1

f(-2) = 1

f(2) = 1 (Ya que f(x) es independiente de x)

f(-2) = f(2) = 1

Por lo tanto probado

Pregunta 22. Demuestra que Lim _x→∞ [√(x ² + x + 1) – x] ≠ Lim _x→∞ [√(x ² + 1) – x]

Solución:

Tenemos,

LHS,

= Lim _x→∞ [√(x ² + x + 1) – x]

Al racionalizar el numerador, obtenemos

= Límite _x→∞ [(x ² + x + 1) – x ² ]/[√(x ² + x + 1) + x]

= Lim _x→∞ (x + 1)/[√(x ² + x + 1) + x]

= Lim _x→∞ [x(1 + 1/x)/[x{√(1 + 1/x + 1/x ² ) + 1}]

= Lim _x→∞ [(1 + 1/x)/[{√(1 + 1/x + 1/x ² ) + 1}]

Cuando x → ∞, (1/x), (1/x ² ) → 0.

= 1/(√1 + 1)

= 1/2

Ahora resolvemos RHS,

= Lim _x→∞ [√(x ² + 1) – x]

Al racionalizar el numerador, obtenemos

= Límite _x→∞ [(x ² + 1) – x ² ]/[√(x ² + 1) + x]

= Lim _x→∞ (1)/[√(x ² + 1) + x]

= 1/[√(∞ + 1) + ∞]

= 1/∞

= 0

IZQ ≠ DERECHO

Por lo tanto, Lim _x→∞ [√(x ² + x + 1) – x] ≠ Lim _x→∞ [√(x ² + 1) – x]

Pregunta 23. Lim _x→-∞ [√(4x ² – 7x) + 2x]

Solución:

Tenemos,

Límite _x→-∞ [√(4x ² – 7x) + 2x]

Sea x = -n cuando x → -∞, entonces n → ∞.

= Lím _n→∞ [√(4n ² + 7n) – 2n]

Al racionalizar el numerador, obtenemos

= Lim _n→∞ [(4n ² + 7n) – 4n ² ]/[√(4n ² + 7n) + 2n]

= Lim _n→∞ [(7n)/[√(4n ² + 7n) + 2n]

= Lim _n→∞ (7n)/[n{√(4 + 7/n) + 2}]

= Lim _n→∞ (7)/{√(4 + 7/n) + 2}

Cuando n → ∞, (1/n) → 0

= 7/(√4 + 2)

= 7/(2 + 2)

= 7/4

Pregunta 24. Lim _x→-∞ [√(x ² – 8x) + x]

Solución:

Tenemos,

Límite _x→-∞ [√(x ² – 8x) + x]

Sea x = -n cuando x → -∞, entonces n → ∞.

= Lim _n→∞ [√(n ² + 8n) – n]

Al racionalizar el numerador, obtenemos

= Lim _n→∞ [(n ² + 8n) – n ² ]/[√(n ² + 8n) + n]

= Lim _n→∞ [(8n)/[√(n ² + 8n) + n]

= Lim _n→∞ (8n)/[n{√(1 + 8/n) + 1}]

= Lim _n→∞ (8)/{√(1 + 8/n) + 1}

Cuando n → ∞, (1/n) → 0

= 8/(√1 + 1)

= 8/2

= 4

Pregunta 25. Lim _n→∞ (1 ⁴ + 2 ⁴ + ……….+ n ⁴ )/n ⁵ – Lim _n→∞ (1 ³ + 2 ³ + ………. + n ³ )/n ⁵

Solución:

Tenemos,

Lím _n→∞ (1 ⁴ + 2 ⁴ + ……….+ n ⁴ )/n ⁵ – Lím _n→∞ (1 ³ + 2 ³ + ………. + n ³ )/n ⁵

= $\lim_{n\to∞}\frac{\frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}}{n^5}-\lim_{n\to∞}\frac{\frac{n^2(n+1)^2}{4}}{n^5}$

= $\lim_{n\to∞}\frac{n(n+1)(2n+1)(3n^2+3n-1)}{30n^5}-\lim_{n\to∞}\frac{n^2(n+1)^2}{4n^5}$

= $\lim_{n\to∞}\frac{(n+1)(2n+1)(3n^2+3n-1)}{30n^4}-\lim_{n\to∞}\frac{(n+1)^2}{4n^3}$

= $\frac{1}{30}\lim_{n\to∞}(1+\frac{1}{n})(2+\frac{1}{n})(3+\frac{3}{n}-\frac{1}{n^2})-\frac{1}{4}\lim_{n\to∞}\frac{1}{n}(1+\frac{1}{n})^2$

Cuando n → ∞, (1/n), (1/n ² ), (1/n ³ ) → 0

= 1/3 × 1 × 2 × 3 – 1/4 × 0

= 6/30

= 1/5

Pregunta 26. Lim _n→∞ {(1.2 + 2.3 + 3.4 + ……….+ n (n + 1)}/n ³

Solución:

Tenemos,

Lím _n→∞ {(1.2 + 2.3 + 3.4 + ……….+ n (n + 1)}/n ³

= $\lim_{n\to∞}\frac{\frac{n(n+1)(2n+1)}{6}+\frac{n(n+1)}{2}}{n^3}$

= $\lim_{n\to∞}\frac{n(n+1)[\frac{(2n+1)+3}{6}]}{n^3}$

= $\lim_{n\to∞}\frac{n(n+1)[\frac{(2n+4)}{6}]}{n^3}$

= $\lim_{n\to∞}\frac{n(n+1)[(2n+4)]}{6n^3}$

= $\lim_{n\to∞}\frac{n(n+1)[(2n+4)]}{6n^3}$

= $\lim_{n\to∞}\frac{(1+\frac{1}{n})(2+\frac{4}{n})}{6}$

Cuando n → ∞, (1/n) → 0

= (1 × 2)/6

= 2/6

= 1/3

Publicación traducida automáticamente

Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 RD Sharma Solutions – Capítulo 29 Límites – Ejercicio 29.6 | conjunto 2

Pregunta 14. Lim _n→∞ {1 ² + 2 ² + ……………. + n ² }/(n ³ )

Pregunta 15. Lim _n→∞ {1 + 2 + 3 + 4 +………………. + n – 1}/n ²

Pregunta 16. Lim _n→∞ {1 ³ + 2 ³ + ……………. + n ³ }/(n ⁴ )

Pregunta 17. Lim _n→∞ {1 ³ + 2 ³ + ……………. + n ³ }/(n – 1) ⁴

Pregunta 18. Lim _x→∞ [√x{√(x + 1) – √x}]

Pregunta 19. Lim _x→∞ [1/3 + 1/3 ² + 1/3 ³ + ……………… + 1/3 ⁿ ]

Pregunta 20. Lim _x→∞ {(x ⁴ + 7x ³ + 46x + a)}/{(x ⁴ + 6)}.

Pregunta 21. f(x) = (ax ² + b)/(x ² + 1), Lim _x→0 f(x) = 1, Lim _x→∞ f(x) = 1, luego prueba que f(- 2) = f(2) = 1

Pregunta 22. Demuestra que Lim _x→∞ [√(x ² + x + 1) – x] ≠ Lim _x→∞ [√(x ² + 1) – x]

Pregunta 23. Lim _x→-∞ [√(4x ² – 7x) + 2x]

Pregunta 24. Lim _x→-∞ [√(x ² – 8x) + x]

Pregunta 25. Lim _n→∞ (1 ⁴ + 2 ⁴ + ……….+ n ⁴ )/n ⁵ – Lim _n→∞ (1 ³ + 2 ³ + ………. + n ³ )/n ⁵

Pregunta 26. Lim _n→∞ {(1.2 + 2.3 + 3.4 + ……….+ n (n + 1)}/n ³

Deja una respuesta Cancelar la respuesta

Pregunta 14. Lim n→∞ {1 2 + 2 2 + ……………. + n 2 }/(n 3 )

Pregunta 15. Lim n→∞ {1 + 2 + 3 + 4 +………………. + n – 1}/n 2

Pregunta 16. Lim n→∞ {1 3 + 2 3 + ……………. + n 3 }/(n 4 )

Pregunta 17. Lim n→∞ {1 3 + 2 3 + ……………. + n 3 }/(n – 1) 4

Pregunta 18. Lim x→∞ [√x{√(x + 1) – √x}]

Pregunta 19. Lim x→∞ [1/3 + 1/3 2 + 1/3 3 + ……………… + 1/3 n ]

Pregunta 20. Lim x→∞ {(x 4 + 7x 3 + 46x + a)}/{(x 4 + 6)}.

Pregunta 21. f(x) = (ax 2 + b)/(x 2 + 1), Lim x→0 f(x) = 1, Lim x→∞ f(x) = 1, luego prueba que f(- 2) = f(2) = 1

Pregunta 22. Demuestra que Lim x→∞ [√(x 2 + x + 1) – x] ≠ Lim x→∞ [√(x 2 + 1) – x]

Pregunta 23. Lim x→-∞ [√(4x 2 – 7x) + 2x]

Pregunta 24. Lim x→-∞ [√(x 2 – 8x) + x]

Pregunta 25. Lim n→∞ (1 4 + 2 4 + ……….+ n 4 )/n 5 – Lim n→∞ (1 3 + 2 3 + ………. + n 3 )/n 5

Pregunta 26. Lim n→∞ {(1.2 + 2.3 + 3.4 + ……….+ n (n + 1)}/n 3

Deja una respuesta Cancelar la respuesta

Pregunta 14. Lim _n→∞ {1 ² + 2 ² + ……………. + n ² }/(n ³ )

Pregunta 15. Lim _n→∞ {1 + 2 + 3 + 4 +………………. + n – 1}/n ²

Pregunta 16. Lim _n→∞ {1 ³ + 2 ³ + ……………. + n ³ }/(n ⁴ )

Pregunta 17. Lim _n→∞ {1 ³ + 2 ³ + ……………. + n ³ }/(n – 1) ⁴

Pregunta 18. Lim _x→∞ [√x{√(x + 1) – √x}]

Pregunta 19. Lim _x→∞ [1/3 + 1/3 ² + 1/3 ³ + ……………… + 1/3 ⁿ ]

Pregunta 20. Lim _x→∞ {(x ⁴ + 7x ³ + 46x + a)}/{(x ⁴ + 6)}.

Pregunta 21. f(x) = (ax ² + b)/(x ² + 1), Lim _x→0 f(x) = 1, Lim _x→∞ f(x) = 1, luego prueba que f(- 2) = f(2) = 1

Pregunta 22. Demuestra que Lim _x→∞ [√(x ² + x + 1) – x] ≠ Lim _x→∞ [√(x ² + 1) – x]

Pregunta 23. Lim _x→-∞ [√(4x ² – 7x) + 2x]

Pregunta 24. Lim _x→-∞ [√(x ² – 8x) + x]

Pregunta 25. Lim _n→∞ (1 ⁴ + 2 ⁴ + ……….+ n ⁴ )/n ⁵ – Lim _n→∞ (1 ³ + 2 ³ + ………. + n ³ )/n ⁵

Pregunta 26. Lim _n→∞ {(1.2 + 2.3 + 3.4 + ……….+ n (n + 1)}/n ³