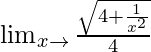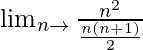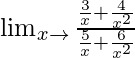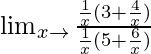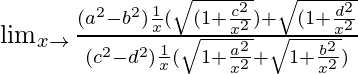Pregunta 1. Lim x→∞ {(3x – 1)(4x – 2)}/{(x + 8)(x – 1)}.
Solución:
Tenemos,
Límite x→∞ {(3x – 1)(4x – 2)}/{(x + 8)(x – 1)}
=
=
Cuando x → ∞, (1/x) → 0.
= (3 × 4)/(1 × 1)
= 12
Pregunta 2. Lim x→∞ {(3x 3 – 4x 2 + 6x – 1)}/{(2x 3 + x 2 – 5x + 7)}.
Solución:
Tenemos,
Lim x→∞ {(3x 3 – 4x 2 + 6x – 1)}/{(2x 3 + x 2 – 5x + 7)}
=
=
Cuando x → ∞, (1/x), (1/x 2 ), (1/x 3 ) → 0.
= 3/2
Pregunta 3. Lim x→∞ {(5x 3 – 6)}/{√(9 + 4x 6 )}.
Solución:
Tenemos,
Límite x→∞ {(5x 3 – 6)}/{√(9 + 4x 6 )}
=
=
Cuando x → ∞, (1/x), (1/x 3 ) → 0.
= 5/√4
= 5/2
Pregunta 4. Lim x→∞ {√(x 2 + cx) – x}
Solución:
Tenemos,
Lim x→∞ {√(x 2 +cx)-x}
Al racionalizar el numerador, obtenemos
= Lim x→∞ {(x 2 + cx) – x 2 }/{√(x 2 + cx) + x}
= Lim x→∞ (cx)/{√(x 2 + cx) + x}
= Lim x→∞ (cx)/[x{√(x + c/x) + 1}]
= Lim x→∞ (c)/{√(1 + c/x) + 1}
Cuando x → ∞, (1/x) → 0.
= c/(√1 + 1)
= c/2
Pregunta 5. Lim x→∞ {√(x + 1) – √x}
Solución:
Tenemos,
Lim x→∞ {√(x + 1) – √x}
Al racionalizar el numerador, obtenemos
= Lim x→∞ {(x+1)-x}/{√(x+1)+√x}
= Lim x→∞ (1)/{√(x+1)+√x}
=
Cuando x → ∞, (1/x) → 0.
= 0
Pregunta 6. Lim x→∞ {√(x 2 + 7x) – x}
Solución:
Tenemos,
Lim x→∞ {√(x 2 + 7x) – x}
Al racionalizar el numerador, obtenemos
= Lim x→∞ {(x 2 +7x)-x2}/{√(x 2 +7x)+x}
= Limx→∞(7x)/{√(x 2 +7x)+x}
=
=
Cuando x → ∞, (1/x) → 0.
= 7/(√1 + 1)
= 7/2
Pregunta 7. Lim x→∞ (x)/{√(4x 2 + 1) – 1}
Solución:
Tenemos,
Lim x→∞ (x)/{√(4x 2 + 1) – 1}
Racionalización del denominador.
= Lim x→∞ [x{√(4x 2 + 1) + 1}]/{(4x 2 + 1) – 1}
= Lim x→∞ [x{√(4x 2 + 1) + 1}]/(4x 2 )
= Lim x→∞ [{√(4x 2 + 1) + 1}]/(4x)
=
Cuando x → ∞, (1/x 2 ) → 0.
= √4/4
= 2/4
= 1/2
Pregunta 8. Lim n→∞ (n 2 )/{1 + 2 + 3 + 4 + ……………. + n}
Solución:
Tenemos,
Lim n→∞ (n 2 )/{1 + 2 + 3 + 4 + ……………. + n}
=
= Lím n→∞ (2n)/(n+1)
= Lím n→∞ (2)/(1+1/n)
Cuando n → ∞, (1/n) → 0
= 2/(1 + 0)
= 2
Pregunta 9. Lim x→∞ (3x -1 + 4x -2 )/(5x -1 + 6x -2 )
Solución:
Tenemos,
Lim x→∞ (3x -1 + 4x -2 )/(5x -1 + 6x -2 )
=
=
Cuando x → ∞, (1/x) → 0.
= 3/5
Pregunta 10. Lim x→∞ {√(x 2 + a 2 ) – √(x 2 + b 2 )}/{√(x 2 + c 2 ) – √(x 2 + d 2 )}
Solución:
Tenemos,
Lim x→∞ {√(x 2 + a 2 ) – √(x 2 + b 2 )}/{√(x 2 + c 2 ) – √(x 2 + d 2 )}
Al racionalizar numerador y denominador, obtenemos
=
=
=
=
Cuando x → ∞, (1/x 2 ) → 0.
=
= (a 2 – b 2 )/(c 2 – d 2 )
Pregunta 11. Lim n→∞ {(n + 2)! + (n + 1)!}/{(n + 2)! – (n + 1)!}.
Solución:
Tenemos,
Lím n→∞ {(n + 2)! + (n + 1)!}/{(n + 2)! – (n + 1)!}
= Lím n→∞ {(n + 2)(n + 1)! + (n + 1)!}/{(n + 2)(n + 1)! – (n + 1)!}
= Lim n→∞ [(n + 1)!{(n + 2) + 1}]/[(n + 1)!{(n + 2) – 1}]
= Lím n→∞ (n + 3)/(n + 1)
= Lím n→∞ [n(1 + 3/n)]/[n(1 + 1/n)]
Cuando n → ∞, (1/n) → 0.
= 1/1
= 1
Pregunta 12. Lim x→∞ [x{√(x 2 + 1) – √(x 2 – 1)}]
Solución:
Tenemos,
Límite x→∞ [x{√(x 2 + 1) – √(x 2 – 1)}]
Al racionalizar el numerador, obtenemos
= Lim x→∞ [x{(x 2 + 1) – (x 2 – 1)}]/{√(x 2 + 1) + √(x 2 – 1)}
= Lim x→∞ (2x)/{√(x 2 + 1) + √(x 2 – 1)}
= Lim x→∞ (2x)/[x{√(1 + 1/x 2 ) + √(1 – 1/x 2 )}]
= Lim x→∞ (2)/[{√(1 + 1/x 2 ) + √(1 – 1/x 2 )}]
Cuando x → ∞, (1/x 2 ) → 0.
= 2/(√1 + √1)
= 2/2
= 1
Pregunta 13. Lim x→∞ [√(x + 2){√(x + 1) – √x}]
Solución:
Tenemos,
Lim x→∞ [√(x + 2){√(x + 1) – √x}]
Al racionalizar el numerador, obtenemos
= Lim x→∞ [√(x + 2){(x + 1) – x}]/{√(x + 1) + √x}
= Lim x→∞ [√(x + 2)]/{√(x + 1) + √x}
= Lim x→∞ [x√(1 + 2/x)]/[x{√(1 + 1/x) + √1}]
= Lim x→∞ [√(1 + 2/x)]/{√(1 + 1/x) + √1}
Cuando x → ∞, (1/x) → 0.
= 1/(√1 + √1)
= 1/2
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
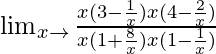
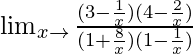
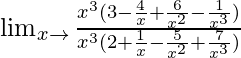
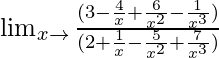
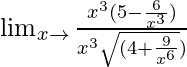
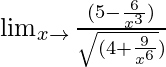
![Rendered by QuickLaTeX.com \lim_{x\to∞}\frac{7x}{x[\sqrt{(1+\frac{7}{x}})+1]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-146289dfc9655e2d3430127a8678f62e_l3.png)
![Rendered by QuickLaTeX.com \lim_{x\to∞}\frac{7}{[\sqrt{(1+\frac{7}{x}})+1]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-149a929c04a05b14839e13abcc97e5e6_l3.png)