Pregunta 1. 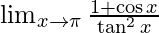
Solución:
Dado,
Aplicando límites, obtenemos,
⇒
=
(Forma indeterminada o forma 0/0)
Entonces, no podemos simplemente aplicar directamente los límites ya que obtuvimos una forma indeterminada.
Al sustituir
obtenemos,
⇒
Sabemos,
⇒ sí
⇒
Usando obtenemos,
⇒
⇒
Aplicando límites obtenemos,
⇒
⇒
Por lo tanto, el valor de
Pregunta 2. 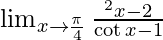
Solución:
Dado,
Aplicando los límites, obtenemos,
⇒
(Forma indeterminada)
Entonces, no podemos simplemente aplicar directamente los límites ya que obtuvimos una forma indeterminada.
Sabemos,
⇒
⇒
⇒
Al usar la fórmula, obtenemos,
⇒
⇒
Aplicando los límites, obtenemos,
⇒
Por lo tanto, el valor de
Pregunta 3.
Solución:
Dado,
Aplicando los límites, obtenemos,
⇒
(Forma indeterminada)
Lo sabemos, ⇒
⇒
⇒
Al usar la fórmula, obtenemos,
⇒
⇒
Aplicando los límites, obtenemos,
⇒
Por lo tanto, el valor de
Pregunta 4. 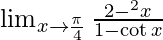
Solución:
Dado,
Aplicando los límites que obtenemos,
⇒
(Forma indeterminada)
Entonces, no podemos simplemente aplicar los límites.
Lo sabemos, ⇒
⇒
⇒
Al usar la fórmula, obtenemos,
⇒
⇒
Aplicando los límites que obtenemos,
⇒
Por lo tanto, el valor de
Pregunta 5.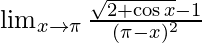
Solución:
Dado,
Aplicando los límites, obtenemos,
⇒
(Forma indeterminada)
Entonces, no podemos simplemente aplicar los límites.
Racionalizando el numerador (multiplicando y dividiendo con
)
⇒
⇒
Dejar
Si
Sustituyendo obtenemos,
⇒
Sabemos que sustituyendo obtenemos,
⇒
Usando ⇒
⇒
⇒
Lo sabemos,
Aplicando los límites, obtenemos,
⇒
⇒ 1/2 x 1/2 = 1/4
Por lo tanto, el valor de
Pregunta 6.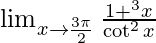
Solución:
Dado,
Aplicando los límites, obtenemos,
⇒
(Forma indeterminada)
Entonces, no podemos simplemente aplicar directamente los límites,
Al usar la fórmula, obtenemos,
⇒
Usando la fórmula,
⇒
⇒
Aplicando los límites, obtenemos,
⇒
Por lo tanto, el valor de
Publicación traducida automáticamente
Artículo escrito por srinivasteja18 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
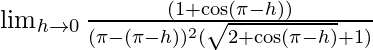
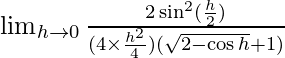
![Rendered by QuickLaTeX.com \frac{1}{2} \lim_{h \to 0}[(\frac{\sin (\frac{h}{2})}{(\frac{h}{2})})^2\times(\frac{1}{\sqrt{2-\cos h}+1)})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fe2a47eb2b8e7f8b7dd848a3a1bc04ad_l3.png)
