Clase 11 RD Sharma Solutions – Capítulo 3 Funciones – Ejercicio 3.2

Pregunta 1. Si f(x)=x ² -3x+4, entonces encuentra los valores de x que satisfacen la ecuación f(x)=f(2x+1).

Solución:

Tenemos,

f(x)=x ² -3x+4

Ahora,

f(2x+1)=(2x+1) ² -3(2x+1)+4

f(2x+1)=4x ² +1+4x-6x-3+4

f(2x+1)=4×2 -2x+ ²

se da que

f(x)=f(2x+1)

x2 -3x+4=4×2 ^-2x + ²

0=4x ² -x ² -2x+3x+2-4

3x ² +x-2=0

3x ² +3x-2x-2=0

3x(x+1)-2(x+1)=0

(x+1)(3x-2)=0

x+1=0 o 3x-2=0

x=-1 o x=2/3

Por lo tanto, el valor de x son -1 y 2/3.

Pregunta 2. Si f(x)=(xa) ² (xb) ² , encuentra f(a+b).

Solución:

Tenemos,

f(x)=(xa) ² (xb) ²

Ahora encontremos f(a+b)

f(a+b)=(a+ba) ² (a+bb) ²

f(a+b)=b ² a ²

Por lo tanto, f(a+b)=(ba) ²

Pregunta 3. Si y=f(x)=(ax-b)/(bx-a), demuestre que x=f(y).

Solución:

Dado,

y=f(x)=(ax-b)/(bx-a)

Como sabemos, f(y)=(ay-b)/(by-a)

Probemos que x=f(y).

Tenemos,

y=(ax-b)/(bx-a)

Al multiplicar en cruz,

y(bx-a)=ax-b

bxy-ay=ax-b

bxy-ax=ay-b

x(by-a)=ay-b

x=(ay-b)/(por-a)

Por lo tanto, x=f(y)

Por lo tanto probado.

Pregunta 4. Si f (x) = 1 / (1 – x), demuestre que f [f {f (x)}] = x.

Solución:

Dado:

f (x) = 1 / (1 – x)

Probemos que f [f {f (x)}] = x.

En primer lugar, resolvamos para f {f (x)}.

f {f (x)} = f {1/(1 – x)}

= 1 / 1 – (1/(1 – x))

= 1 / [(1 – x – 1)/(1 – x)]

= 1 / (-x/(1 – x))

= (1 – x) / -x

= (x – 1) / x

∴ f {f (x)} = (x – 1) / x

Ahora, resolveremos para f [f {f (x)}]

f [f {f (x)}] = f [(x-1)/x]

= 1 / [1 – (x-1)/x]

= 1 / [(x – (x-1))/x]

= 1 / [(x – x + 1)/x]

= 1 / (1/x)

∴ f [f {f (x)}] = x

Por lo tanto probado.

Pregunta 5. Si f (x) = (x + 1) / (x – 1), demuestre que f [f (x)] = x.

Solución:

Dado:

f (x) = (x + 1) / (x – 1)

Tenemos que demostrar que f [f (x)] = x.

f [f (x)] = f [(x+1)/(x-1)]

= [(x+1)/(x-1) + 1] / [(x+1)/(x-1) – 1]

= [[(x+1) + (x-1)]/(x-1)] / [[(x+1) – (x-1)]/(x-1)]

= [(x+1) + (x-1)] / [(x+1) – (x-1)]

= (x+1+x-1)/(x+1-x+1)

= 2x/2

= x

∴ f [f (x)] = x

Por lo tanto probado.

Pregunta 6. Si

$f(x) = \begin{cases} x^2,\text{when } x<0\\ x, \text{when }0\leq x<1\\ \frac{1}{x},\text{when }x\geq1 \end{cases}$

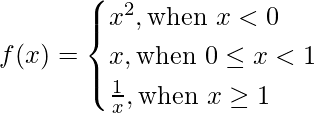
Encontrar:

(yo) f (1/2)

(ii) f (-2)

(iii) f (1)

(iv) f (√3)

(v) f (√-3)

Solución:

(yo) f (1/2)

Cuando, 0 ≤ x ≤ 1, f(x) = x

∴ f (1/2) = 1/2

(ii) f (-2)

Cuando, x < 0, f(x) = x ²

f (–2) = (–2) ²

= 4

∴ f (–2) = 4

(iii) f (1)

Cuando, x ≥ 1, f (x) = 1/x

f(1) = 1/1

∴f(1) = 1

(iv) f (√3)

Tenemos √3 = 1.732 > 1

Cuando, x ≥ 1, f (x) = 1/x

∴ f (√3) = 1/√3

(v) f (√-3)

Sabemos que √-3 no es un número real y que la función f(x) está definida solo cuando x ∈ R.

∴ f (√-3) no existe.

Pregunta 7. Si f(x)=x ³ -(1/x ³ ), demuestra que f(x)+f(1/x)=0.

Solución:

Tenemos,

f(x)=x ³ -(1/x) ³ —(i)

Ahora,

f(1/x)=(1/x) ³ -(1/(1/x) ³ )

f(1/x)=(1/x) ³ -x ³ —(ii)

Sumando las ecuaciones (i) y (ii), obtenemos

f(x)+f(1/x) = (x ³ -1/x ³ )+(1/x ³ -x ³ )

f(x)+f(1/x)=x ³ -x ³ +1/x ³ -1/x ³

f(x)+f(1/x)=0

Por lo tanto, probado.

Pregunta 8. Si f(x)= 2x/(1+x ² ), demuestra que f(tan θ)=sen 2θ .

Solución.

Tenemos,

f(x)=2x/(1+x ² )

Ahora,

f(tan θ)=2(tan θ)/(1+tan ² θ)

f(tan θ)=sen 2θ (Porque, sen 2θ = 2(tan θ)/(1+tan ² θ))

Por lo tanto, probado.

Pregunta 9. Si f(x)=(x-1)/(x+1), entonces demuestre que

i) f(1/x)=-f(x)

ii) f(1/(-x))=-1/f(x)

Solución.

i) Tenemos,

f(x)=(x-1)/(x+1)

Ahora,

f(1/x)=((1/x)-1)/((1/x)+1)

f(1/x)=((1-x)/x)/((1+x)/x)

f(1/x)=(1-x)/(1+x)=f(-x)

Por lo tanto, probado.

ii) Tenemos,

f(x)=(x-1)/(x+1)

Ahora,

f(1/(-x))= ((1/(-x))-1)/((1/(-x))+1)

f(1/(-x))=((1+x)/(-x))/((1-x)/(-x))

f(1/(-x))=(1+x)/(1-x)

f(1/(-x))=(-1)/((x-1)/(x+1))

f(1/(-x))=-1/f(x)

Por lo tanto, probado.

Pregunta 10. Si f(x)=(ax ⁿ ) ^1/n ,a>0 y n ∈ N, entonces demuestre que f(f(x))=x para todo x.

Solución.

Tenemos,

$f(x)=(a-x^n)^\frac{1}{n}, a>0\\ \newline \\ Now, \\ f(f(x))=f(a-x^n)^\frac{1}{n}\\ f(f(x))=[a-\{(a-x^n)^\frac{1}{n}\}^n]^\frac{1}{n} \\ f(f(x))=[a-(a-x^n)]^\frac{1}{n}\\ f(f(x))=[a-a+x^n]^\frac{1}{n}\\ f(f(x))=(x^n)^\frac{1}{n}\\ f(f(x))=x\\ Hence, proved$

Pregunta 11. Si para x distinto de cero, af(x)+bf(1/x) = 1/x – 5, donde a ≠ b, entonces encuentre f(x).

Solución.

Tenemos,

$af(x)+bf(\frac{1}{x})=\frac{1}{x}-5$ -(i)

$af(\frac{1}{x})+bf(x)=\frac{1}{\frac{1}{x}}-5\\ af(\frac{1}{x})+bf(x)=x-5$

$af(\frac{1}{x})+bf(x)=x-5$ —(ii)

Sumando las ecuaciones (i) y (ii), obtenemos

$af(x)+bf(x)+bf(\frac{1}{x})+af(\frac{1}{x})=\frac{1}{x}-5+x-5\\ (a+b)f(x)+f(\frac{1}{x})(a+b)=\frac{1}{x}+x-10$

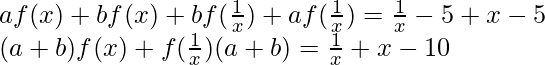
$f(x)+f(\frac{1}{x})=\frac{1}{a+b}[\frac{1}{x}+x-10]$ —(iii)

Restar la ecuación (ii) de la ecuación (i)

$af(x)-bf(x )+bf(\frac{1}{x})-af(\frac{1}{x})=\frac{1}{x}-5-x+5 \\ (a-b)f(x)-f(\frac{1}{x})(a-b)=\frac{1}{x}-x \\ f(x)-f(\frac{1}{x})=\frac{1}{a-b}[\frac{1}{x}-x]$ —(iv)

Sumando las ecuaciones (iii) y (iv), obtenemos

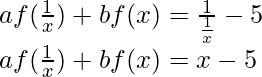
$2f(x)=\frac{1}{a+b}[\frac{1}{x}+x-10]+\frac{1}{a-b}[\frac{1}{x}-x]\\ 2f(x)=\frac{(a-b)[\frac{1}{x}+x-10]+(a+b)[\frac{1}{x}-x]}{(a+b)(a-b)} \\ 2f(x)=\frac{\frac{a}{x}+ax-10a-\frac{b}{x}-bx+10b+\frac{a}{x}-ax+\frac{b}{x}-bx}{a^2-b^2} \\ 2f(x)=\frac{\frac{2a}{x}-10a+10b-2bx}{a^2-b^2} \\ f(x)=\frac{1}{a^2-b^2}\times\frac{1}{2}[\frac{2a}{x}-10a+10b-2bx]\\ f(x)=\frac{1}{a^2-b^2}[\frac{a}{x}-5a+5b-bx]$

Por lo tanto,

$f(x)=\frac{1}{a^2-b^2}[\frac{a}{x}-5a+5b-bx]$