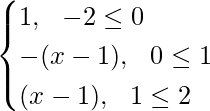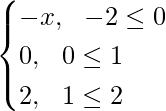Pregunta 1. Encuentra f + g, f – g, cf (c ∈ R, c ≠ 0), fg, 1/f y f/g en cada uno de los siguientes:
(i) f(x) = x 3 + 1 y g (x) = x + 1
Solución:
Dado, f(x) = x 3 + 1 y g(x) = x + 1 y f(x): R → R y g(x): R → R
Sabemos, (f + g)(x) = f(x) + g(x) ⇒ (f + g) (x) = x 3 + 1 + x + 1 = x 3 + x + 2
Entonces, (f + g)(x) = x 3 + x + 2
Como, (f – g)(x) = f(x) – g(x) ⇒ (f – g)(x) = x 3 + 1 – (x + 1) = x 3 + 1 – x – 1 = x 3 –x
Entonces, (f – g)(x) = x 3 – x
Además, (cf)(x) = c × f(x) ⇒ (cf)(x) = c(x 3 + 1) = cx 3 + c
Entonces, (cf)(x) = cx 3 + c
Dado que, (fg)(x) = f(x)g(x) ⇒ (fg)(x) = (x 3 + 1)(x + 1) = (x + 1) (x 2 – x + 1) (x + 1) = (x + 1) 2 (x 2 – x + 1)
Entonces, (fg)(x) = (x + 1) 2 (x 2 – x + 1)
Ahora, (1/f)(x) = 1/f (x) ⇒ 1/f (x) = 1/(x 3 + 1)
Como 1/f(x) no está definido cuando f(x) = 0 o cuando x = – 1,
Por tanto, 1/f: R – {–1} → R viene dado por 1/f (x) = 1 / (x 3 + 1)
Por último, (f/g)(x) = f(x)/g(x) ⇒ (f/g) (x) = (x 3 + 1)/(x + 1)
Dado que (x 3 + 1)/(x + 1) no está definido cuando g(x) = 0 o cuando x = –1.
Como x 3 + 1 = (x + 1)(x 2 – x + 1), tenemos (f/g)(x) =
= x 2 – x + 1
Por tanto, f/g: R – {–1} → R viene dado por (f/g)(x) = x 2 – x + 1
(ii) f(x) = 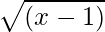 y g(x) =
y g(x) = 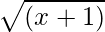
Solución:
Dado que la raíz cuadrada real se define solo para números no negativos, f(x): [1, ∞) → R+ y g(x): [–1, ∞) → R+
Sabemos, (f + g)(x) = f(x) + g(x) =
+
Dominio de (f + g) = Dominio de f ∩ Dominio de g = [1, ∞) ∩ [–1, ∞) = [1, ∞)
Por tanto, f + g: [1, ∞) → R viene dado por (f + g)(x) =
+
Como, (f – g)(x) = f(x) – g(x) =
–
Dominio de (f – g) = Dominio de f ∩ Dominio de g = [1, ∞) ∩ [–1, ∞) = [1, ∞)
Por tanto, f – g: [1, ∞) → R viene dado por (f – g)(x) =
–
Dado que, (cf)(x) = c × f(x) = c
Dominio de (cf) = Dominio de f = [1, ∞)
Por tanto, cf: [1, ∞) → R viene dado por (cf)(x) = c
Además, (fg)(x) = f(x)g(x) =
=
Dominio de (fg) = Dominio de f ∩ Dominio de g = [1, ∞) ∩ [–1, ∞) = [1, ∞)
Por lo tanto, fg: [1, ∞) → R viene dado por (fg)(x) =
Ahora, (1/f) (x) = 1/f(x) =
Dominio de (1/f) = Dominio de f = [1, ∞)
Dado
que tampoco está definido cuando x – 1 = 0 o x = 1.
Por tanto, 1/f: (1, ∞) → R viene dado por (1/f)(x) =
Por último, (f/g) (x) = f(x)/g(x) =
Dominio de (f/g) = Dominio de f ∩ Dominio de g = [1, ∞) ∩ [–1, ∞) = [1, ∞)
Por tanto, f/g: [1, ∞) → R viene dado por (f/g) (x) =
Pregunta 2. Sean f(x) = 2x + 5 y g(x) = x 2 + x. Describe y encuentra el dominio en cada uno:
(yo) f + g
Solución:
Dado, f(x) = 2x + 5 y g(x) = x 2 + x
Tanto f(x) como g(x) están definidas para todo x ∈ R.
Entonces, dominio de f = dominio de g = R
Sabemos, (f + g)(x) = f(x) + g(x) ⇒ (f + g)(x) = 2x + 5 + x 2 + x
= x2 + 3x + 5
Dado que (f + g)(x) está definido para todos los números reales x.
Por lo tanto, (f + g)(x) = x 2 + 3x + 5 y el dominio de (f + g) es R.
(ii) f – g
Solución:
Como (f – g)(x) = f(x) – g(x) ⇒ (f – g)(x)
= 2x + 5 – (x2 + x)
= 2x + 5 – x 2 – x
= 5 + x – x 2
Dado que (f – g)(x) está definido para todos los números reales x.
Por lo tanto, (f – g)(x) = 5 + x – x 2 y el dominio de (f – g) es R.
(iii) fg
Solución:
Sabemos, (fg)(x) = f(x)g(x) ⇒ (fg)(x) = (2x + 5)(x 2 + x)
= 2x(x2 + x) + 5(x2 + x )
= 2x 3 + 2x 2 + 5x 2 + 5x
= 2x 3 + 7x 2 + 5x
Dado que (fg)(x) está definido para todos los números reales x.
Por lo tanto, (fg)(x) = 2x 3 + 7x 2 + 5x y el dominio de fg es R.
(iv) f/g
Solución:
Sabemos, (f/g) (x) = f(x)/g(x) ⇒ (f/g)(x) =
Claramente (f/g)(x) se define para todos los valores reales de x, excepto en el caso en que x 2 + x = 0.
x 2 + x = 0 ⇒ x(x + 1) = 0 ⇒ x = 0 o x + 1 = 0 ⇒ x = 0 o –1
Cuando x = 0 o –1, (f/g)(x) no estará definido.
Por lo tanto, El dominio de f/g = R – {–1, 0}
Pregunta 3. Si f(x) se define en [–2, 2] y está dada por 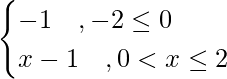 y g(x) = f(|x|) + |f(x)|. Encuentre g(x).
y g(x) = f(|x|) + |f(x)|. Encuentre g(x).
Solución:
f(|x|) = |x| – 1, donde –2 ≤ x ≤ 2
y, |f(x)| =
Así, g(x) = f(|x|) + |f(x)| =
Pregunta 4. Sean f, g dos funciones reales definidas por f(x) = 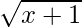 y g(x) =
y g(x) = 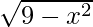 . Luego, describe cada una de las siguientes funciones.
. Luego, describe cada una de las siguientes funciones.
(yo) f + g
Solución:
Dado, f(x) =
y g(x) =
f(x) toma valores reales solo cuando x + 1 ≥ 0 x ≥ –1, x ∈ [–1, ∞) ⇒ Dominio de f = [–1, ∞)
g(x) toma valores reales solo cuando 9 – x 2 ≥ 0
⇒ x 2 ≤ 9 ⇒ x 2 – 3 2 ≤ 0 ⇒ (x + 3)(x – 3) ≤ 0
⇒ x ≥ –3 y x ≤ 3
⇒ Dominio de g = [–3, 3]
Sabemos, (f + g)(x) = f(x) + g(x) ⇒ (f + g) (x) =
+
Dominio de f + g = Dominio de f ∩ Dominio de g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
Por tanto, f + g: [–1, 3] → R viene dado por (f + g)(x) = f(x) + g(x) =
+
(ii) g – f
Solución:
Sabemos, (g – f)(x) = g(x) – f(x) ⇒ (g – f)(x) =
–
Dominio de g – f = Dominio de g ∩ Dominio de f = [–3, 3] ∩ [–1, ∞) = [–1, 3]
Por tanto, g – f: [–1, 3] → R viene dado por (g – f) (x) = g(x) – f(x) =
–
(iii) fg
Solución:
Sabemos, (fg)(x) = f(x)g(x) ⇒ (fg)(x) =
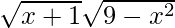
=
=
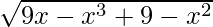
=
Dominio de fg = Dominio de f ∩ Dominio de g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
Por tanto, fg: [–1, 3] → R viene dado por (fg) (x) = f(x) g(x) =
=
(iv) f/g
Solución:
Sabemos, (f/g) (x) = f(x)/g(x) ⇒ (f/g) (x) =
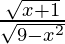
Dominio de f/g = Dominio de f ∩ Dominio de g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
Sin embargo, (f/g) (x) se define para todos los valores reales de x ∈ [–1, 3], excepto en el caso en que 9 – x2 = 0 o x = ± 3
Cuando x = ±3, (f/g) (x) será indefinido ya que el resultado de la división será indeterminado.
Dominio de f/g = [–1, 3] – {–3, 3} = [–1, 3)
Por tanto, f/g: [–1, 3) → R viene dado por (f/g) (x) = f(x)/g(x) =
(v) g/m
Solución:
Sabemos, (g/f)(x) = g(x)/f(x) ⇒ (g/f)(x) =
Dominio de g/f = Dominio de f ∩ Dominio de g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
Sin embargo, (g/f) (x) está definida para todos los valores reales de x ∈ [–1, 3], excepto en el caso en que x + 1 = 0 o x = –1
Cuando x = –1, (g/f) (x) será indefinido ya que el resultado de la división será indeterminado.
Dominio de g/f = [–1, 3] – {–1} = (–1, 3]
Por tanto, g/f: (–1, 3] → R viene dado por (g/f) (x) = g(x)/f(x) =
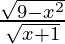
(vi) 2f – √5 g
Solución:
Sabemos, (2f – √5g)(x) = 2f(x) – √5g(x)
⇒ (2f – √5g)(x) = 2f (x) – √5g(x)
= 2
–
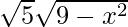
= 2
–
Dominio de 2f – √5g = Dominio de f ∩ Dominio de g = [–1, ∞) ∩ [–3, 3] = [–1, 3]
Por tanto, 2f – √5g: [–1, 3] → R viene dado por (2f – √5g) (x) = 2f(x) – √5 g(x) = 2
–
(vii) f 2 + 7f
Solución:
Sabemos, (f 2 + 7f)(x) = f 2 (x) + (7f)(x)
⇒ (f 2 + 7f) (x) = f(x).f(x) + 7f(x)
=
+ 7
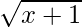
= X + 1 + 7
El dominio de f 2 + 7f es igual que el dominio de f = [–1, ∞)
Por tanto, f 2 + 7f: [–1, ∞) → R viene dado por (f2 + 7f) (x) = f(x) f(x) + 7f(x) = x + 1 + 7
(viii) 5/g
Solución:
Sabemos, (5/g)(x) = 5/g(x) ⇒ (5/g)(x) =
Dominio de 5/g = Dominio de g = [–3, 3]
Sin embargo, (5/g)(x) se define para todos los valores reales de x ∈ [–3, 3], excepto en el caso en que 9 – x 2 = 0 o x = ± 3
Cuando x = ±3, (5/g)(x) no estará definido.
Por tanto, Dominio de 5/g = [–3, 3] – {–3, 3} = (–3, 3)
Por tanto, 5/g: (–3, 3) → R viene dado por (5/g)(x) = 5/g(x) =
Pregunta 5. Si f(x) = log e (1 – x) y g(x) = [x], determine cada una de las siguientes funciones:
(yo) f + g
Solución:
f(x) = log e (1 – x) y g(x) = [x]
Sabemos que f(x) toma valores reales solo cuando 1 – x > 0 o cuando 1 > x
x < 1, ∴ x ∈ (–∞, 1) ⇒ Dominio de f = (–∞, 1)
g(x) está definida para todos los números reales x. ⇒ Dominio de g = [x], x ∈ R = R
Así, (f + g)(x) = f(x) + g(x) = log e (1 – x) + [x]
Dominio de f + g = Dominio de f ∩ Dominio de g = (–∞, 1) ∩ R = (–∞, 1)
Por tanto, f + g: (–∞, 1) → R viene dado por (f + g) (x) = log e (1 – x) + [x]
(ii) fg
Solución:
Sabemos, (fg)(x) = f(x)g(x) ⇒ (fg)(x) = log e (1 – x) × [x] = [x]log e (1 – x)
Dominio de fg = Dominio de f ∩ Dominio de g = (–∞, 1) ∩ R = (–∞, 1)
Por tanto, fg: (–∞, 1) → R viene dado por (fg) (x) = [x] log e (1 – x).
(iii) f/g
Solución:
Sabemos, (f/g)(x) = f(x)/g(x) ⇒ (f/g)(x) =
Dominio de f/g = Dominio de f ∩ Dominio de g = (–∞, 1) ∩ R = (–∞, 1)
Sin embargo, (f/g) (x) está definida para todos los valores reales de x ∈ (–∞, 1), excepto cuando [x] = 0.
Tenemos, [x] = 0 cuando 0 ≤ x < 1 o x ∈ [0, 1)
Cuando 0 ≤ x < 1, (f/g) (x) será indefinido. Dominio de f/g = (–∞, 1) – [0, 1) = (–∞, 0)
Por tanto, f/g: (–∞, 0) → R viene dado por (f/g)(x) =
(iv) g/m
Solución:
Sabemos, (g/f)(x) = g(x)/f(x) ⇒ (g/f)(x) =
Sin embargo, (g/f)(x) está definida para todos los valores reales de x ∈ (–∞, 1), excepto en el caso de que loge (1 – x) = 0.
⇒ logaritmo (1 – x) = 0 ⇒ 1 – x = 1
o x = 0
Cuando x = 0, (g/f) (x) será indefinido ya que el resultado de la división será indeterminado.
Dominio de g/f = (–∞, 1) – {0} = (–∞, 0) ∪ (0, 1)
Por tanto, g/f: (–∞, 0) ∪ (0, 1) → R viene dado por (g/f)(x) =
(v) (f + g)(–1)
Solución:
(f + g) (x) = log e (1 – x) + [x], x ∈ (–∞, 1)
Sustituyendo x = –1 en la ecuación anterior, obtenemos
(f + g)(–1) = log e (1 – (–1)) + [–1]
= log e (1 + 1) + (–1)
= log e 2 – 1
Por lo tanto, (f + g)(–1) = log e 2 – 1
(vi) (fg)(0)
Solución:
Tenemos, (fg)(x) = [x]log e (1 – x), x ∈ (–∞, 1)
Sustituyendo x = 0 en la ecuación anterior, obtenemos
(fg)(0) = [0] log e (1 – 0)
= 0 × log e 1 = 0
Por lo tanto, (fg) (0) = 0
(vii) (f/g)(1/2)
Solución:
(f/g)(x) =
, x ∈ (–∞, 0)
Sin embargo, 1/2 no está en el dominio de f/g.
Por lo tanto, (f/g)(1/2) no existe.
(viii) (f) (1/2)
Solución:
Tenemos, (g/f)(x) =
, x ∈ (–∞, 0) ∪ (0, ∞)
Sustituyendo x=1/2 en la ecuación anterior, obtenemos
(g/f)(1/2) =
=
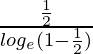
=
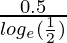
=
= 0
Por lo tanto, (g/f)(1/2) = 0
Pregunta 6. Si f, g, h son funciones reales definidas por f(x) = 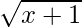 , g(x) = 1/x y h(x) = 2x 2 – 3, entonces encuentre los valores de (2f + g – h )(1) y (2f + g – h)(0).
, g(x) = 1/x y h(x) = 2x 2 – 3, entonces encuentre los valores de (2f + g – h )(1) y (2f + g – h)(0).
Solución:
Como f(x) está definida para x + 1 ≥ 0 ⇒ x ≥ – 1
⇒ x ∈ [– 1, ∞] = Dominio de f(x)
Ahora, (2f+g –h)(x) = 2f(x) + g(x) – h(x)
= 2
+ 1/x – (2x 2 – 3)
= 2
+ 1/1 – 2(1) 2 + 3
(2f + g – h)(x) = 2√2 + 2
Como (2f+g –h)(0) no pertenece al dominio x ∈ [– 1, ∞] – 0, no existe.
Pregunta 7. La función f(x) está definida por: f(x) = 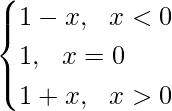 . Dibujar la gráfica de f(x).
. Dibujar la gráfica de f(x).
Solución:
La gráfica de f(x) para x < 0 se encuentra a la izquierda del origen.
La gráfica de f(x) para x > 0 se encuentra a la derecha del origen.
La gráfica de f(x) para x = 0 está representada por el punto (0,1).
Pregunta 8. Sean f, g: R ⇒ R respectivamente como f(x) = x + 1 y g(x) = 2x – 3. Halla f + g, f – g y f/g.
Solución:
Sabemos, (f + g)(x) = f(x) + g(x) = (x + 1 + 2x – 3) = 3x – 2.
Ahora, (f – g)(x) = f(x) – g(x) = (x + 1) – (2x – 3) = 4 – x.
f/g(x) = f(x)/g(x) =
Pregunta 9. Sean f y g respectivamente como f(x) = √x y g(x) = x. Encuentre f + g, f – g, fg y f/g.
Solución:
(f + g)(x) = f(x) + g(x) = √x + x
(f – g)(x) = f(x) – g(x) = √x – x
(fg)(x) = f(x)g(x) = √xx = x 1/2 + 1 = x 3/2
f/g(x) = f(x)/g(x) = √x/x = 1/√x
Pregunta 10. Sean f(x) = x 2 y g(x) = 2x + 1 dos funciones reales. Encuentre f + g, f – g, fg y f/g.
Solución:
(f + g)(x) = f(x) + g(x) = x 2 + 2x + 1 = (x + 1) 2
(f – g)(x) = f(x) – g(x) = x 2 – 2x – 1
(fg)(x) = f(x)g(x) = x 2 (2x + 1) = 2x 3 + x 2
f/g(x) = f(x)/g(x) =
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA