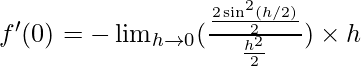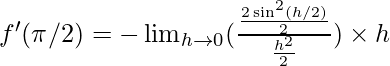Clase 11 RD Sharma Solutions- Capítulo 30 Derivados – Ejercicio 30.1

Posted on by Rudeus Greyrat

Pregunta 1. Encuentra la derivada de f(x) = 3x en x = 2

Solución:

Dado: f(x)=3x

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {donde h es un pequeño número positivo}

La derivada de f(x)=3x en x=2 se da como:

f'(2)= \lim_{h \to 0} \frac {f(2+h)-f(2)} h

⇒ f'(2)= \lim_{h \to 0} \frac {3(2+h)-3(2)} h

⇒ f'(2)= \lim_{h \to 0} \frac {3h+6-6} h

⇒ f'(2)= \lim_{h \to 0} \frac {3h} h

⇒ f'(2)= \lim_{h \to 0} 3 = 3

Por lo tanto, la derivada de f(x)=3x en x=2 es 3

Pregunta 2. Encuentra la derivada de f(x) = x 2 – 2 en x = 10

Solución:

Dado: f(x)= x 2 -2 

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {donde h es un pequeño número positivo}

La derivada de f(x)=x 2 -2 en x=10 se da como:

f'(10)= \lim_{h \to 0} \frac {f(10+h)-f(10)} h

⇒f'(10)= \lim_{h \to 0} \frac {(100+h^2+20h-2-100+2))} h

⇒f'(10)= \lim_{h \to 0} \frac {h^2+20h} h

⇒f'(10)= \lim_{h \to 0} \frac {h(h+20)} h

⇒f'(10)= \lim_{h \to 0} {h+20}

⇒f'(10)= 0+20=20

Por lo tanto, la derivada de f(x)=x 2 -2 en x=10 es 20

Pregunta 3. Encuentra la derivada de f(x) = 99x en x = 100

Solución:

Dado: f(x)= 99x

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {donde h es un pequeño número positivo}

La derivada de f(x)=99x en x=100 se da como:

f'(100)= \lim_{h \to 0} \frac {f(100+h)-f(100)} h

⇒ f'(100)= \lim_{h \to 0} \frac {99(100+h)-99(100)} h

⇒ f'(100)= \lim_{h \to 0} \frac {9900+99h-9900} h

⇒ f'(100)= \lim_{h \to 0} 99 = 99

Por lo tanto, la derivada de f(x)=99x en x=100 es 99

Pregunta 4. Encuentra la derivada de f(x) = x en x = 1

Solución:

Dado: f(x)=x

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h {donde h es un pequeño número positivo}

La derivada de f(x)=x en x=1 se da como:

f'(1)= \lim_{h \to 0} \frac {f(1+h)-f(1)} h

⇒ f'(1)= \lim_{h \to 0} \frac {(1+h)-1} h

⇒ f'(1)= \lim_{h \to 0} \frac {h} h

⇒f'(1)= \lim_{h \to 0} 1 = 1

Por lo tanto, la derivada de f(x)=x en x=1 es 1

Pregunta 5. Encuentra la derivada de f(x) = 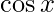 \cos x  en x = 0

Solución:

Dado: f(x)=\cos x

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h {donde h es un pequeño número positivo}

La derivada de f(x)= \cos x  en x=0 se da como:

f'(0)= \lim_{h \to 0} \frac {f(0+h)-f(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\cos(0+h)-\cos(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\cos(h)-\cos(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\cos(h)-1} h

∵ no podemos encontrar el límite de la función anterior f(x)= \cos x  por sustitución directa ya que da la forma 0/0 (forma indeterminada)

Así que lo simplificaremos para encontrar el límite.

Como sabemos que 1 - \cos x = 2 \sin2(x/2)

∴ f'(0)= \lim_{h \to 0} \frac {-(1-\cos(h))} h = - \lim_{h \to 0} \frac {2\sin^2(h/2)} h

Divide el numerador y el denominador por 2 para obtener la forma  \sin x/x  de aplicar el teorema del sándwich y multiplicar h en el numerador y el denominador para obtener la forma requerida.

⇒ f'(0)= -\lim_{h \to 0}( \frac {\frac {2\sin^2(h/2)}2} {\frac {h^2}2}) \times h

⇒ f'(0)= -\lim_{h \to 0}( \frac {\sin(h/2)} {\frac {h}2}) \times \lim_{h \to 0}h

Usando la fórmula: \lim_{x \to 0} \frac{\sin x}x=1

∴ f'(0)=-1 \times 0=0

Por lo tanto, la derivada de f(x)= \cos x  en x=0 es 0

Pregunta 6. Encuentra la derivada de f(x) = 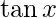 \tan x  en x = 0

Solución:

Dado: f(x)=\tan x

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h {donde h es un pequeño número positivo}

La derivada de f(x)= \tan x  en x=0 se da como:

f'(0)= \lim_{h \to 0} \frac {f(0+h)-f(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\tan(0+h)-\tan(0)} h

⇒ f'(0)= \lim_{h \to 0} \frac {\tan(h)-0} h

⇒ f'(0)= \lim_{h \to 0} \frac {\tan(h)} h

∴ Usa la fórmula:  \lim_{x \to 0} \frac {\tan x} x=1  {teorema del sándwich}

⇒ f'(0)=1

Por lo tanto, la derivada de f(x)= \tan x  en x=0 es 1

Pregunta 7(i). Encuentre las derivadas de las siguientes funciones en los puntos indicados: 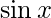 \sin x  en x=\pi/2

Solución:

Dado: f(x)= \sin x

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h {donde h es un pequeño número positivo}

La derivada de f(x)= \sin x  at  x=\pi/2  se da como:

f'(\pi/2)= \lim_{h \to 0} \frac {f(\pi/2+h)-f(\pi/2)} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {\sin(\pi/2+h)-\sin(\pi/2)} h

⇒  f'(\pi/2)= \lim_{h \to 0} \frac {\sin(\pi/2+h)-1} h

⇒ f'(\pi/2)=  \lim_{h \to 0} \frac {\cos(h)-1} h   {∵\sin(\pi/2+x)=\cos x

∵ no podemos encontrar el límite de la función anterior por sustitución directa ya que da la forma 0/0 (forma indeterminada)

Así que lo simplificaremos para encontrar el límite.

Como sabemos que

1 - \cos x = 2 \sin^2(x/2)

∴ f'(\pi/2)= \lim_{h \to 0} \frac {-(1-\cos(h))} h = - \lim_{h \to 0} \frac {2\sin^2(h/2)} h

Divide el numerador y el denominador por 2 para obtener la forma (sen x)/x para aplicar el teorema del sándwich y multiplicar h en el numerador y el denominador para obtener la forma requerida.

⇒ f'(\pi/2)= -\lim_{h \to 0}( \frac {\frac {2\sin^2(h/2)}2} {\frac {h^2}2}) \times h

⇒ f'(\pi/2)= -\lim_{h \to 0}( \frac {\sin(h/2)} {\frac {h}2}) \times \lim_{h \to 0}h

Usando la fórmula:

\lim_{x \to 0} \frac{\sin x}x=1

∴ f'(\pi/2)=-1 \times 0=0

Por lo tanto, la derivada de f(x)=  \sin x  at  x=\pi/2  es 0

Pregunta 7(ii). Encuentre las derivadas de las siguientes funciones en los puntos indicados: x en x=1

Solución:

Dado: f(x)=x

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {donde h es un pequeño número positivo}

La derivada de f(x)=x en x=1 se da como:

f'(1)= \lim_{h \to 0} \frac {f(1+h)-f(1)} h

⇒ f'(1)= \lim_{h \to 0} \frac {(1+h)-1} h

⇒ f'(1)= \lim_{h \to 0} \frac {h} h

⇒ f'(1)= \lim_{h \to 0} 1 = 1

Por lo tanto, la derivada de f(x)=x en x=1 es 1

Pregunta 7(iii). Encuentre las derivadas de las siguientes funciones en los puntos indicados: 2\cos x en x=\pi/2

Solución:

Dado: f(x)= 2\cos x

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {donde h es un pequeño número positivo}

La derivada de f(x)=  2\cos x  at  x=\pi/2  se da como:

f'(\pi/2)= \lim_{h \to 0} \frac {f(\pi/2+h)-f(\pi/2)} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {2\cos(\pi/2+h)-2cos(\pi/2)} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {-2\sin(h)} h {∵  \cos(\pi/2+x)=-\sin x }

∵ no podemos encontrar el límite de la función anterior por sustitución directa ya que da la forma 0/0 (forma indeterminada)

∴  f'(\pi/2)= -2\lim_{h \to 0} \frac {\sin h} h

Usando la fórmula:  \lim_{x \to 0} \frac{\sin x}x=1

∴ f'(\pi/2)=-2 \times 1=-2

Por lo tanto, derivada de f(x)= 2\cos x =-2

Pregunta 7(iv). Encuentre las derivadas de las siguientes funciones en los puntos indicados: 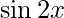 \sin 2x  en x=\pi/2

Solución:

Dado: f(x)= \sin 2x

Usando la fórmula de la derivada,

f'(a)= \lim_{h \to 0} \frac {f(a+h)-f(a)} h  {donde h es un pequeño número positivo}

La derivada de f(x)=  \sin 2x  at  x=\pi/2  se da como:

f'(\pi/2)= \lim_{h \to 0} \frac {f(\pi/2+h)-f(\pi/2)} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {\sin 2(\pi/2+h)-sin 2(\pi/2)} h

⇒  f'(\pi/2)= \lim_{h \to 0} \frac {\sin(\pi+2h) - \sin \pi} h  {∵ \sin(\pi+x)=-sinx }

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {-\sin(2h) - 0} h

⇒ f'(\pi/2)= \lim_{h \to 0} \frac {-\sin(2h)} h

∵ no podemos encontrar el límite de la función anterior por sustitución directa ya que da la forma 0/0 (forma indeterminada)

Usando el teorema del sándwich y multiplicando 2 en numerador y denominador para aplicar la fórmula.

f'(\pi/2)= -\lim_{h \to 0} \frac {\sin(2h)} {2h} \times 2 = -2\lim_{h \to 0} \frac {\sin(2h)} {2h}

Usando la fórmula: \lim_{x \to 0} \frac{\sin x}x=1

∴ f'(\pi/2)=-2 \times 1=-2

Por lo tanto, derivada de f(x)=\sin 2x=-2  

Publicación traducida automáticamente

Artículo escrito por manandeep1610 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *