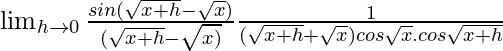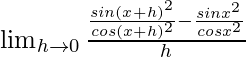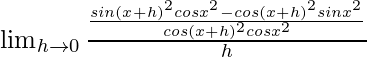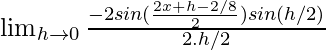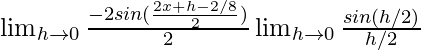Pregunta 3. Diferencie cada uno de los siguientes usando primeros principios:
(i) xsinx
Solución:
Dado que f(x) = xsenx
Usando la fórmula
Obtenemos
=
=
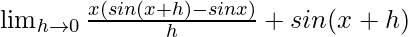
Usando la fórmula
sinc – sind = 2cos((c + d)/2)sin((c – d)/2)
Obtenemos
=
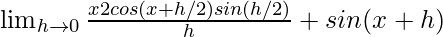
Como sabemos que
Asi que,
= 2x × cosx × 1/2 + senx
= x × cosx + senx
= senx + xcosx
(ii) x cos x
Solución:
Dado que f(x) = xcosx
Usando la fórmula
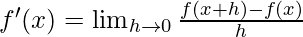
Obtenemos
=
=
=
=
=
= -xsenx + cosx
(iii) sen(2x – 3)
Solución:
Dado que f(x) = sin(2x – 3)
Usando la fórmula
Obtenemos
=
=
Usando la fórmula
sinC – sinD = 2cos{C+D}/2sin{CD}/2
=
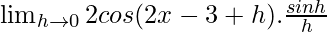
Como sabemos que, \lim_{θ\to 0}\frac{sinθ}{θ}=1 entonces,
= 2cos(2x – 3)
(iv) √sen2x
Solución:
Dado que f(x) = √sin2x
Usando la fórmula
Obtenemos
=
Al multiplicar numerador y denominador por
obtenemos
=
=
=
=
=
(v) senx/x
Solución:
Dado que f{x} = senx/x
Usando la fórmula
Obtenemos
=
=
=
=
=
h ⇢ 0 ⇒ h/2 ⇢ 0 y
=
=
(vi) cosx/x
Solución:
Dado que f(x) = cosx/x
Usando la fórmula
Obtenemos
=
=
=
=
=
=
=
(vii) x 2 senx
Solución:
Dado que f(x) = x 2 senx
Usando la fórmula
Obtenemos
=
=
=
=
= 0 + [2xsenx + x 2 cosx]
= 2xsenx + x 2 cosx
(viii) 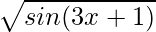
Solución:
Dado que f(x) =
Usando la fórmula
Obtenemos
=
=
=
=
=
(ix) senx + cosx
Solución:
Dado que f(x) = senx + cosx
Usando la fórmula
Obtenemos
=
=
=
=
=
=
= cosx – senx
Pregunta 4. Diferencie cada uno de los siguientes usando primeros principios:
(i) broncearse 2 veces
Solución:
Dado que f(x) = tan 2 x
Usando la fórmula
Obtenemos
=
=
=
=
=
=
=
= 2tanx seg 2 x
(ii) tan(2x + 1)
Solución:
Dado que f(x) = tan(2x+1)
Usando la fórmula
Obtenemos
=
=
=
Multiplicando numerador y denominador por 2.
=
=
= 2seg 2 (2x+1)
(iii) tan2x
Solución:
Dado que f(x) = tan2x
Usando la fórmula
Obtenemos
=
=
=
=
=
= 2 seg 2 2x
(iv) √tanx
Solución:
Dado que f(x) = √tanx
Usando la fórmula
Obtenemos
=
Al multiplicar numerador y denominador por
Obtenemos
=
=
=
=
=
Pregunta 5. Diferencie cada uno de los siguientes usando primeros principios:
(i) 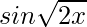
Solución:
Dado que f(x) =
Usando la fórmula
Obtenemos
=
=
=
=
=
=
(ii) cos√x
Solución:
Dado que f(x) = cos√x
Usando la fórmula
Obtenemos
=
=
=
Multiplicar numerador y denominador por
=
=
=
=
(iii) tan√x
Solución:
Dado que f(x) = tan√x
Usando la fórmula
Obtenemos
=
=
=
=
=
=
=
=
(iv) tango 2
Solución:
Dado que f(x) = tanx 2
Usando la fórmula
Obtenemos
=
=
=
=
=
=
=
=
= 2xseg 2 x 2
Pregunta 6. Diferencie cada uno de los siguientes usando primeros principios:
(yo) -x
Solución:
Dado que f(x) = -x
Usando la fórmula
Obtenemos
=
=
= -1
(ii) (-x) -1
Solución:
Dado que f(x) = (-x) -1
Usando la fórmula
Obtenemos
=
=
=
= 1/ x2
(iii) sen(x + 1)
Solución:
Dado que f(x) = sin(x+1)
Usando la fórmula
Obtenemos
=
=
=
=
=
= cos(x+1)
(iv) cos(x – π/8)
Solución:
Tenemos, f(x) = cos(x – π/8)
Usando la fórmula
Obtenemos
=
=
=
=
=
=
= -sen(x + π/8)
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \lim_{h\to 0}x.2sin(x-x+h/2)sin(x+h/2)+cos(x+h) [cosA-cosB=2sin(\frac{B-A}{2})sin(\frac{B+A}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d6447bf9b23ed3075f5fed9dfc40a65f_l3.png)
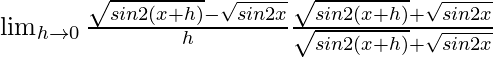
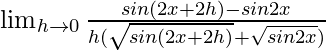
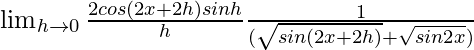
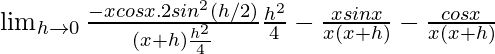
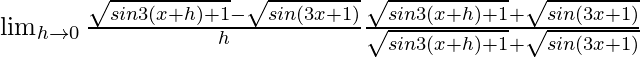
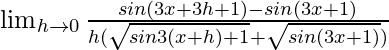
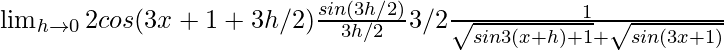
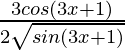
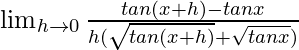
![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{sin(x+h-x)}{h.cos(x+h)cosx[\sqrt{tan(x+h)}+\sqrt{tanx}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-786cfa2381a724019862fee1051fcf1b_l3.png)
![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{2sin[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]cos[\frac{\sqrt{2(x+h)}+\sqrt{2x}}{2}]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c807e1f9a661ef7d3e0a18a36db46f1_l3.png)
![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{sin[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}{[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}\frac{(\sqrt{2(x+h)}-\sqrt{2x})(\sqrt{2(x+h)}+\sqrt{2x})}{(\sqrt{2(x+h)}+\sqrt{2x})h}cos[\frac{\sqrt{2(x+h)+2x}}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8c36845e81daadfdc771f002c7c8e066_l3.png)
![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{sin[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}{[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}\lim_{h\to 0}\frac{{2(x+h)}-2x}{(\sqrt{2(x+h)}+\sqrt{2x})h}\lim_{h\to 0}cos[\frac{\sqrt{2(x+h)+2x}}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5d2c2901d1934e9a32e8b08649358bfe_l3.png)
![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{-2sin[\frac{\sqrt{x+h}-\sqrt{x}}{2}][\sqrt{x+h}-\sqrt{x}[\sqrt{x+h}+\sqrt{x}]}{h[\frac{\sqrt{x+h}-\sqrt{x}}{2}][\sqrt{x+h}+\sqrt{x}]}×sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bf72051f52d104bd445cf8108a0a2416_l3.png)
![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{-sin[\frac{\sqrt{x+h}-\sqrt{x}}{2}]}{[\frac{\sqrt{x+h}-\sqrt{x}}{2}]}×\frac{x+h-x}{(\sqrt{x+h}+\sqrt{x})h}×sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c45b9cee19296e3a43860e921c03c742_l3.png)