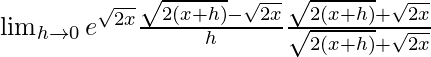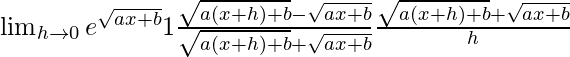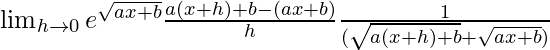Pregunta 1. Diferencie cada uno de los siguientes usando primeros principios:
(yo) 2/x
Solución:
Dado que f(x) = 2/x
Usando la fórmula
f'(x) =
Obtenemos
=
=
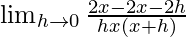
=
=
=
(ii) 1/√x
Solución:
Dado que f(x) = 1/√x
Usando la fórmula
Obtenemos
=
=
=
=
=
=
=
=
(iii) 1/x 3
Solución:
Tenemos f(x) = 1/x 3
Usando la fórmula
Obtenemos
=
=
=
=
=
=
(iv) (x 2 + 1)/x
Solución:
Dado que f(x) = (x 2 + 1)/x
Usando la fórmula
Obtenemos
=
=
=
=
=
=
(v) (x 2 – 1)/x
Solución:
Dado que f(x) = (x 2 – 1)/x
Usando la fórmula
Obtenemos
=
=
=
=
=
(vi) (x + 1)/(x + 2)
Solución:
Dado que f(x) = (x + 1)/(x + 2)
Usando la fórmula
Obtenemos
=
=
=
= 1/(x + 2) 2
(vii) (x + 2)/(3x + 5)
Solución:
Dado que f(x) = (x + 2)/(3x + 5)
Usando la fórmula
Obtenemos
=
=
=
=
=
=
(viii) kx n
Solución:
Dado que f(x) = kx n
Usando la fórmula
Obtenemos
=
=
=
= k nx n-1 + 0 + 0 …
= k n x n-1
(ix) 1/√(3 – x)
Solución:
Dado que f(x) = 1/√(3-x)
Usando la fórmula
Obtenemos
=
=
=
=
=
=
=
(x) x 2 + x + 3
Solución:
Dado que f(x) = x 2 + x + 3
Usando la fórmula
Obtenemos
=
=
=
=
= 2x + 0 + 1
= 2x + 1
(xi) (x + 2) 3
Solución:
Dado que f(x) = (x + 2) 3
Usando la fórmula
Obtenemos
=
=
=
=
= 3(x + 2) 2
(xii) x 3 + 4x 2 + 3x + 2
Solución:
Dado que f(x) = x 3 + 4x 2 + 3x + 2
Usando la fórmula
Obtenemos
=
=
=
=
= 3x 2 + 8x + 3
(xiii) (x 2 + 1) (x – 5)
Solución:
Dado que f(x) = (x 2 +1)(x-5)
Usando la fórmula
Obtenemos
=
=
=
=
= 3x 2 – 10x + 1
(xiv) √(2x 2 + 1)
Solución:
Dado que f(x) = √(2x 2 + 1)
Usando la fórmula
Obtenemos
=
Al multiplicar numerador y denominador por
Obtenemos
=
=
=
=
=
(xv) (2x + 3)/(x – 2)
Solución:
Dado que f(x) = (2x + 3)/(x – 2)
Usando la fórmula
Obtenemos
=
=
=
=
Pregunta 2. Diferencie cada uno de los siguientes usando primeros principios:
(i) e- x
Solución:
Dado que f(x) = e -x
Usando la fórmula
Obtenemos
=
=
=
= -e -x
(ii) y 3x
Solución:
Dado que f(x) = e 3x
Usando la fórmula
Obtenemos
=
=
=
Multiplicar numerador y denominador por 3.
=
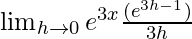
Aquí,
= 3e 3x
(iii) eax+b
Solución:
Dado que f(x) = e ax+b
Usando la fórmula
Obtenemos
=
=
=
=
Al multiplicar numerador y denominador por un
Ya que
= ae ax+b
(iv) xe x
Solución:
Dado que f(x) = xe x
Usando la fórmula
Obtenemos
=
=
=
= xe x + e x
= e x (x + 1)
(v) x 2 e x
Solución:
Dado que f(x) = x 2 e x
Usando la fórmula
Obtenemos
=
=
= x 2 e x + e x (0 + 2x)
= x 2 e x + 2xe x
= e x (x 2 + 2x)
(vi) 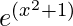
Dado que f(x) =
Usando la fórmula
Obtenemos
=
=
=
=
=
=
(vii) e √(2x)
Solución:
Dado que f(x) =
Usando la fórmula
Obtenemos
=
=
=
Al multiplicar numerador y denominador por
obtenemos
=
Nuevamente multiplicando numerador y denominador por
obtenemos
=
=
(viii) e √(ax + b)
Solución:
Dado que f(x) = e √(ax+b)
Usando la fórmula
Obtenemos
=
=
=
Al multiplicar numerador y denominador por
obtenemos
=
Nuevamente multiplicando numerador y denominador por
obtenemos
=
=
=
(ix) un √x
Solución:
Dado que f(x) = a √x = e √xloga
Usando la fórmula
Obtenemos
=
=
=
Al multiplicar numerador y denominador por
obtenemos
f”(x) =
=
=
Al multiplicar numerador y denominador por
obtenemos
f'(x) =
=
=
=
log ea _
(X) 
Solución:
Dado que f(x) =
Usando la fórmula
Obtenemos
=
=
=
=
=
=
=
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
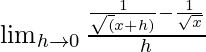
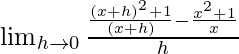

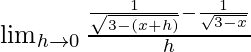
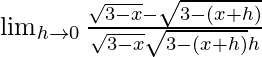

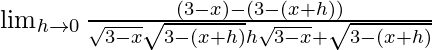
![Rendered by QuickLaTeX.com \lim_{h\to 0}\frac{[2(x+h)^2+1-(2x^2+1)]}{h(\sqrt{2(x+h)^2+1}+\sqrt{2x^2+1})}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-262a4e3c9adb0003bad1d8ea9dfcdf92_l3.png)