Clase 11 Soluciones RD Sharma – Capítulo 30 Derivados – Ejercicio 30.4

Pregunta 11. Diferenciar (x sen x + cos x) (x cos x − sen x) con respecto a x.

Solución:

Tenemos,

=> y = (x sen x + cos x) (x cos x − sen x)

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}[(x sin x + cos x) (x cos x − sin x)]$

Al usar la regla del producto obtenemos,

= $(xcosx−sinx)\frac{d}{dx}(xsinx+cosx)+(xsinx+cosx)\frac{d}{dx}(xcosx-sinx)$

Al usar la regla de la string, obtenemos,

= $(xcosx−sinx)\left[\frac{d}{dx}(xsinx)+\frac{d}{dx}(cosx)\right]+(xsinx+cosx)\left[\frac{d}{dx}(xcosx)-\frac{d}{dx}(sinx)\right]$

Al usar la regla del producto nuevamente, obtenemos,

= $(xcosx−sinx)\left[sinx\frac{d}{dx}(x)+x\frac{d}{dx}(sinx)-sinx\right]+(xsinx+cosx)\left[cosx\frac{d}{dx}(x)+x\frac{d}{dx}(cosx)-cosx\right]$

= $(xcosx−sinx)\left[sinx+xcosx-sinx\right]+(xsinx+cosx)\left[cosx-xsinx-cosx\right]$

= (x cos x − sen x) (x cos x) + (x sen x + cos x) (−x sen x)

= x ² cos ² x − x cos x sen x − x ² sen ² x − x cos x sen x

= x ² (cos ² x − sen ² x) − 2x cos x sen x

= x ² cos 2x − x sen 2x

= x (x cos 2x − sen 2x)

Pregunta 12. Diferenciar (x sen x + cos x) (e ^x + x ² log x) con respecto a x.

Solución:

Tenemos,

=> y = (x sen x + cos x) (e ^x + x ² log x)

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}[(x sin x + cos x) (e^x + x^2 log x)]$

Al usar la regla del producto obtenemos,

= $(e^x + x^2 log x)\frac{d}{dx}(x sin x + cos x)+(x sin x + cos x)\frac{d}{dx}(e^x + x^2 log x)$

Al usar la regla de la string, obtenemos,

= $(e^x + x^2 log x)\left[\frac{d}{dx}(x sin x)+\frac{d}{dx}(cos x)\right]+(x sin x + cos x)\left[\frac{d}{dx}(e^x) + \frac{d}{dx}(x^2 log x)\right]$

Al usar la regla del producto nuevamente, obtenemos,

= $(e^x+x^2log x)\left[sinx\frac{d}{dx}(x)+x\frac{d}{dx}(sinx)-sinx\right]+(xsinx+cosx)\left[e^x+logx\frac{d}{dx}(x^2)+x^2\frac{d}{dx}(logx)\right]$

= $(e^x+x^2log x)\left[sinx+xcosx-sinx\right]+(xsinx+cosx)\left[e^x+2xlogx+x^2(\frac{1}{x})\right]$

= $(e^x+x^2log x)\left(xcosx\right)+(xsinx+cosx)\left[e^x+2xlogx+x\right]$

= (x cos x) (e ^x + x ² log x) +(x sen x + cos x) (e ^x + 2x log x + x)

Pregunta 13. Diferenciar (1 − 2 tan x) (5 + 4 sen x) con respecto a x.

Solución:

Tenemos,

=> y = (1 − 2 tan x) (5 + 4 sen x)

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}[(1−2tanx)(5+4sinx)]$

Al usar la regla del producto obtenemos,

= $(5+4sinx)\frac{d}{dx}(1−2tanx)+(1-2tanx)\frac{d}{dx}(5+4sinx)$

= $(5+4sinx)(−2sec^2x)+(1-2tanx)(4cosx)$

= −10 seg ² x − 8 sen x seg ² x + 4 cos x − 8 tan x cos x

= $−10sec^2x−8sinx(\frac{1}{cos^2x})+4cosx−8(\frac{sinx}{cosx})cosx$

= −10 seg ² x − 8 tan x seg x + 4 cos x − 8 sen x

Pregunta 14. Diferenciar (1 + x ² ) cos x con respecto a x.

Solución:

Tenemos,

=> y = (1 + x ² ) porque x

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}[(1 + x^2) cos x]$

Al usar la regla del producto obtenemos,

= $cosx\frac{d}{dx}[(1 + x^2)]+(1+x^2)\frac{d}{dx}(cosx)$

= cos x (2x) + (1 + x ² ) (−senx)

= 2x cos x − sen x(1 + x ² ) (senx)

Pregunta 15. Diferenciar sen ² x con respecto a x.

Solución:

Tenemos,

=> y = sen ² x

=> y = (sen x) (sen x)

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}[(sin x) (sin x)]$

Al usar la regla del producto obtenemos,

= $sinx\frac{d}{dx}(sinx)+(sinx)\frac{d}{dx}(sinx)$

= sen x cos x + sen x cos x

= 2 sen x cos x

= sen 2x

Pregunta 16. Diferenciar 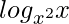$log_{x^2}x$ con respecto a x.

Solución:

Tenemos,

=> y = $log_{x^2}x$

= $\frac{logx}{logx^2}$

= $\frac{logx}{2logx}$

= $\frac{1}{2}$

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(\frac{1}{2})$

= 0

Pregunta 17. Diferenciar 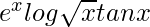$e^xlog\sqrt{x}tanx$ con respecto a x.

Solución:

Tenemos,

=> y = $e^xlog\sqrt{x}tanx$

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(e^xlog\sqrt{x}tanx)$

Al usar la regla del producto obtenemos,

= $log\sqrt{x}tanx\frac{d}{dx}(e^x)+e^x\frac{d}{dx}(log\sqrt{x}tanx)$

Al usar la regla del producto nuevamente, obtenemos,

= $log\sqrt{x}tanx(e^x)+e^x\left[tanx\frac{d}{dx}(log\sqrt{x})+log\sqrt{x}\frac{d}{dx}(tanx)\right]$

= $e^xlog\sqrt{x}tanx+e^x\left[tanx(\frac{1}{\sqrt{x}})(\frac{1}{2\sqrt{x}})+log\sqrt{x}sec^2x\right]$

= $e^xlog\sqrt{x}tanx+e^x\left[\frac{tanx}{2x}+log\sqrt{x}sec^2x\right]$

= $\frac{1}{2}e^xlogxtanx+e^x\left[\frac{tanx}{2x}+\frac{1}{2}logxsec^2x\right]$

= $\frac{e^x}{2}[logxtanx+\frac{tanx}{x}+logxsec^2x]$

Pregunta 18. Diferenciar x ³ e ^x cos x con respecto a x.

Solución:

Tenemos,

=> y = x ³ e ^x porque x

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(x^3e^xcosx)$

Al usar la regla del producto obtenemos,

= $e^xcosx\frac{d}{dx}(x^3)+x^3\frac{d}{dx}(e^xcosx)$

Al usar la regla del producto nuevamente, obtenemos,

= $e^xcosx(3x^2)+x^3[cosx\frac{d}{dx}(e^x)+e^x\frac{d}{dx}(cosx)]$

= $3x^2e^xcosx+x^3[e^xcosx-e^xsinx]$

= $3x^2e^xcosx+x^3e^xcosx-x^3e^xsinx$

= $x^2e^x(3cosx+xcosx-xsinx)$

Pregunta 19. Diferenciar 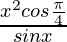$\frac{x^2cos\frac{\pi}{4}}{sinx}$ con respecto a x.

Solución:

Tenemos,

=> y = $\frac{x^2cos\frac{\pi}{4}}{sinx}$

=> y = $x^2cos\frac{\pi}{4}cosecx$

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(x^2cos\frac{\pi}{4}cosecx)$

Al usar la regla del producto obtenemos,

= $cos\frac{\pi}{4}cosecx\frac{d}{dx}(x^2)+x^2\frac{d}{dx}(cos\frac{\pi}{4}cosecx)$

Al usar la regla del producto nuevamente, obtenemos,

= $cos\frac{\pi}{4}cosecx(2x)+x^2[cosecx\frac{d}{dx}(cos\frac{\pi}{4})+cos\frac{\pi}{4}\frac{d}{dx}(cosecx)]$

= $2xcos\frac{\pi}{4}cosecx+x^2[cosecx(0)+cos\frac{\pi}{4}(-cosecxcotx)]$

= $2xcos\frac{\pi}{4}cosecx+x^2[cos\frac{\pi}{4}(-cosecxcotx)]$

= $2xcos\frac{\pi}{4}cosecx-x^2cos\frac{\pi}{4}cosecxcotx$

= $2x(\frac{1}{\sqrt{2}})cosecx-x^2(\frac{1}{\sqrt{2}})cosecxcotx$

= $\frac{xcosecx}{\sqrt{2}}(2-xcotx)$

Pregunta 20. Derive x ⁴ (5 sen x − 3 cos x) con respecto a x.

Solución:

Tenemos,

=> y = x ⁴ (5 sen x − 3 cos x)

Al diferenciar ambos lados, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}[x^4(5sinx−3cosx)]$

Al usar la regla del producto obtenemos,

= $(5sinx−3cosx)\frac{d}{dx}(x^4)+x^4\frac{d}{dx}(5sinx−3cosx)$

= $(5sinx−3cosx)(4x^3)+x^4(5cosx+3sinx)$

= 20 x ³ sen x − 12 x ³ cos x + 5x ⁴ cos x + 3x ⁴ sen x

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 30 Derivados – Ejercicio 30.4 | conjunto 2

Pregunta 11. Diferenciar (x sen x + cos x) (x cos x − sen x) con respecto a x.

Pregunta 12. Diferenciar (x sen x + cos x) (e ^x + x ² log x) con respecto a x.

Pregunta 13. Diferenciar (1 − 2 tan x) (5 + 4 sen x) con respecto a x.

Pregunta 14. Diferenciar (1 + x ² ) cos x con respecto a x.

Pregunta 15. Diferenciar sen ² x con respecto a x.

Pregunta 16. Diferenciar $log_{x^2}x$ con respecto a x.

Pregunta 17. Diferenciar $e^xlog\sqrt{x}tanx$ con respecto a x.

Pregunta 18. Diferenciar x ³ e ^x cos x con respecto a x.

Pregunta 19. Diferenciar $\frac{x^2cos\frac{\pi}{4}}{sinx}$ con respecto a x.

Pregunta 20. Derive x ⁴ (5 sen x − 3 cos x) con respecto a x.

Deja una respuesta Cancelar la respuesta

Pregunta 11. Diferenciar (x sen x + cos x) (x cos x − sen x) con respecto a x.

Pregunta 12. Diferenciar (x sen x + cos x) (e x + x 2 log x) con respecto a x.

Pregunta 13. Diferenciar (1 − 2 tan x) (5 + 4 sen x) con respecto a x.

Pregunta 14. Diferenciar (1 + x 2 ) cos x con respecto a x.

Pregunta 15. Diferenciar sen 2 x con respecto a x.

Pregunta 16. Diferenciar con respecto a x.

Pregunta 17. Diferenciar con respecto a x.

Pregunta 18. Diferenciar x 3 e x cos x con respecto a x.

Pregunta 19. Diferenciar con respecto a x.

Pregunta 20. Derive x 4 (5 sen x − 3 cos x) con respecto a x.

Deja una respuesta Cancelar la respuesta

Pregunta 12. Diferenciar (x sen x + cos x) (e ^x + x ² log x) con respecto a x.

Pregunta 14. Diferenciar (1 + x ² ) cos x con respecto a x.

Pregunta 15. Diferenciar sen ² x con respecto a x.

Pregunta 16. Diferenciar $log_{x^2}x$ con respecto a x.

Pregunta 17. Diferenciar $e^xlog\sqrt{x}tanx$ con respecto a x.

Pregunta 18. Diferenciar x ³ e ^x cos x con respecto a x.

Pregunta 19. Diferenciar $\frac{x^2cos\frac{\pi}{4}}{sinx}$ con respecto a x.

Pregunta 20. Derive x ⁴ (5 sen x − 3 cos x) con respecto a x.