Pregunta 21. Deriva (2x 2 – 3) sen x con respecto a x.
Solución:
Tenemos,
=> y = (2x 2 – 3) sen x
Al diferenciar ambos lados, obtenemos,
Al usar la regla del producto obtenemos,
=
=
=
Pregunta 22. Diferenciar 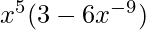 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=> y =
Al diferenciar ambos lados, obtenemos,
Al usar la regla del producto obtenemos,
=
=
=
=
Pregunta 23. Diferenciar 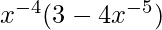 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=> y =
Al diferenciar ambos lados, obtenemos,
Al usar la regla del producto obtenemos,
=
=
=
=
=
=
Pregunta 24. Diferenciar 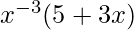 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=> y =
Al diferenciar ambos lados, obtenemos,
Al usar la regla del producto obtenemos,
=
=
=
=
=
Pregunta 25. Diferenciar 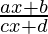 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=> y =
Al diferenciar ambos lados, obtenemos,
Al usar la regla del producto obtenemos,
=
=
=
=
=
=
=
Pregunta 26. Diferenciar (ax + b) n (cx + d) m con respecto a x.
Solución:
Tenemos,
=> y = (ax + b) norte ( cx + d) metro
Al diferenciar ambos lados, obtenemos,
Al usar la regla del producto obtenemos,
=
=
=
=
Pregunta 27. Deriva de dos formas, usando la regla del producto y en caso contrario, la función (1 + 2 tan x) (5 + 4 cos x). Verifica que la respuesta sea la misma.
Solución:
Tenemos,
=> y = (1 + 2 tan x) (5 + 4 cos x)
Al usar la regla del producto obtenemos,
=
= 10 seg 2 x + 8 cos x seg 2 x − 4 sen x − 8 sen x tan x
=
=
=
=
= 10 s 2 x + 8 cos x − 4 sen x
Usando un método alternativo, tenemos,
=
=
Al usar la regla de la string, obtenemos,
= 0 − 4 sen x + 10 seg 2 x + 8 cos x
= 10 s 2 x + 8 cos x − 4 sen x
Por lo tanto probado.
Pregunta 28. Diferencie cada una de las siguientes funciones por la regla del producto y el otro método y verifique que la respuesta de ambos métodos es la misma.
(yo) (3x 2 + 2) 2
Solución:
Tenemos,
=> y = (3x 2 + 2) 2
Al usar la regla del producto obtenemos,
=
= 12x (3x 2 + 2)
= 36×3 + 24x
Usando un método alternativo, tenemos,
Al usar la regla de la string, obtenemos,
= 36×3 + 0 + 24x
= 36×3 + 24x
Por lo tanto probado.
(ii) (x + 2)(x + 3)
Solución:
Tenemos,
=> y = (x + 2)(x + 3)
Al usar la regla del producto obtenemos,
= (x+3)(1)+(x+2)(1)
= x + 3 + x + 2
= 2x + 5
Usando un método alternativo, tenemos,
Al usar la regla de la string, obtenemos,
= 2x + 5
Por lo tanto probado.
(iii) (3 seg x − 4 cosec x) (−2 sen x + 5 cos x)
Solución:
Tenemos,
=> y = (3 seg x − 4 cosec x) (−2 sen x + 5 cos x)
Al usar la regla del producto obtenemos,
= (−2 sen x + 5 cos x) (3 seg x tan x + 4 cot x cosec x)+ (3 seg x − 4 cos x) (−2 cos x − 5 sen x)
= −6 sen x seg x tan x − 8 sen x cot x cosec x + 15 cos x seg x tan x + 20 cos x cot x cosec x − 6 seg x cos x − 15 seg x sen x + 8 cosec x cos x + 20 cosec x sen x
= −6 tan 2 x − 8 cuna x + 15 tan x + 20 cuna 2 x − 6 − 15 tan x + 8 cuna x + 20
= − 6 − 6 bronceado 2 x + 20 cuna 2 x + 20
= −6 (1 + tan 2 x) + 20 (cot 2 x + 1)
= −6 s 2 x + 20 cos 2 x
Usando un método alternativo, tenemos,
=
=
Al usar la regla de la string, obtenemos,
= −6 s 2 x − (−20 cos 2 x)
= −6 s 2 x + 20 cos 2 x
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \frac{d}{dx}[(1 + 2 tan x) (5 + 4 cos x)]=(5 + 4 cos x)\frac{d}{dx}(1+2tanx)+(1+2tanx)\frac{d}{dx}(5+4cosx)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74eb6aa17e6823e5526095cb7d976385_l3.png)
![Rendered by QuickLaTeX.com \frac{d}{dx}[(3secx−4cosecx)(−2sinx+5cosx)]=(−2sinx+5cosx)\frac{d}{dx}(3secx−4cosecx)+(3secx−4cosecx)\frac{d}{dx}(−2sinx+5cosx)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b26fe43f2a1da3341ed84125ea3bfb85_l3.png)
![Rendered by QuickLaTeX.com \frac{d}{dx}[(3secx−4cosecx)(−2sinx+5cosx)]=\frac{d}{dx}(−6secxsinx+15secxcosx+6cosecxsinx-20cosecxcosx)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d205a6270927e418930c6e51ef60a5b3_l3.png)