Clase 11 Soluciones RD Sharma – Capítulo 30 Derivados – Ejercicio 30.4

Pregunta 1. Derive x ³ sen x con respecto a x.

Solución:

Tenemos,

=> y = x ³ sen x

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(x^3sinx)$

Al usar la regla del producto, obtenemos,

= $sinx\frac{d}{dx}(x^3)+x^3\frac{d}{dx}(sinx)$

= senx (3x ² ) + x ³ (cosx)

= 3x ² senx + x ³ cosx

= x ² (3 senx + x cos x)

Pregunta 2. Diferenciar x ³ e ^x con respecto a x.

Solución:

Tenemos,

=> y = x ³ e ^x

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(x^3e^x)$

Al usar la regla del producto, obtenemos,

= $e^x\frac{d}{dx}(x^3)+x^3\frac{d}{dx}(e^x)$

= e ^x (3x ² ) + x ³ (e ^x )

= 3x ² e ^x + x ³ e ^x

= x ² e ^x (3 + x)

Pregunta 3. Derive x ² e ^x log x con respecto a x.

Solución:

Tenemos,

=> y = x ² e ^x log x

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(x^2e^xlog x)$

Al usar la regla del producto, obtenemos,

= $e^xlogx\frac{d}{dx}(x^2)+x^2\frac{d}{dx}(e^xlogx)$

Al usar la regla del producto nuevamente en la segunda parte de la expresión, obtenemos,

= $e^xlogx(2x)+x^2[logx\frac{d}{dx}(e^x)+e^x\frac{d}{dx}(logx)]$

= $e^xlogx(2x)+x^2(e^xlogx+\frac{e^x}{x})$

= $2xe^xlogx+x^2e^xlogx+xe^x$

= $xe^x(2logx+xlogx+1)$

Pregunta 4. Diferenciar x ⁿ tan x con respecto a x.

Solución:

Tenemos,

=> y = x ^norte tan x

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(x^ntanx)$

Al usar la regla del producto, obtenemos,

= $tanx\frac{d}{dx}(x^n)+x^n\frac{d}{dx}(tanx)$

= $tanx(nx^{n-1})+x^n(sec^2x)$

= $nx^{n-1}tanx+x^nsec^2x$

= $x^{n-1}(ntanx+xsec^2x)$

Pregunta 5. Derive x ⁿ log _a x con respecto a x.

Solución:

Tenemos,

=> y = x ^norte log _a x

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(x^nlog_ax)$

Al usar la regla del producto, obtenemos,

= $log_ax\frac{d}{dx}(x^n)+x^n\frac{d}{dx}(log_ax)$

= $log_ax(nx^{n-1})+x^n\frac{d}{dx}(\frac{logx}{loga})$

= $log_ax(nx^{n-1})+\frac{x^n}{loga}(\frac{1}{x})$

= $nx^{n-1}log_ax+\frac{x^{n-1}}{loga}$

= $x^{n-1}\left(nlog_ax+\frac{1}{loga}\right)$

Pregunta 6. Diferenciar (x ³ +x ² +1)senx con respecto a x.

Solución:

Tenemos,

=> y = $(x^3+x^2+1)sinx$

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}[(x^3+x^2+1)sinx]$

Al usar la regla del producto, obtenemos,

= $sinx\frac{d}{dx}(x^3+x^2+1)+(x^3+x^2+1)\frac{d}{dx}(sinx)$

= $sinx(3x^2+2x)+(x^3+x^2+1)(cosx)$

= $3x^2sinx+2xsinx+x^3cosx+x^2cosx+cosx$

Pregunta 7. Diferenciar sen x cos x con respecto a x.

Solución:

Tenemos,

=> y = sen x cos x

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(sinxcosx)$

Al usar la regla del producto, obtenemos,

= $cosx\frac{d}{dx}(sinx)+(sinx)\frac{d}{dx}(cosx)$

= cos x (cos x) − sen x (−sen x)

= cos ² x − sen ² x

= cos ² x − (1 − cos ² x)

= cos ² x − 1 + cos ² x

= 2 cos ² x − 1

= cos 2x

Pregunta 8. Diferenciar 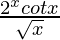$\frac{2^xcotx}{\sqrt{x}}$ con respecto a x.

Solución:

Tenemos,

=> y = $\frac{2^xcotx}{\sqrt{x}}$

=> y = $2^x×cotx×x^{\frac{-1}{2}}$

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{d}{dx}(\frac{2^xcotx}{\sqrt{x}})=\frac{d}{dx}(2^x×cotx×x^{\frac{-1}{2}})$

Al usar la regla del producto, obtenemos,

= $\frac{cotx}{\sqrt{x}}\frac{d}{dx}(2^x)+2^x\frac{d}{dx}(cotx×x^{\frac{-1}{2}})$

Al usar la regla del producto nuevamente en la segunda parte de la expresión, obtenemos,

= $\frac{2^xlog2cotx}{\sqrt{x}}+2^x[x^{\frac{-1}{2}}\frac{d}{dx}(cotx)+cotx\frac{d}{dx}(x^{\frac{-1}{2}})]$

= $\frac{2^xlog2cotx}{\sqrt{x}}+2^x\left[\frac{-cosec^2x}{\sqrt{x}}+\frac{-cotx}{2}\frac{1}{x^{\frac{3}{2}}}\right]$

= $\frac{2^xlog2cotx}{\sqrt{x}}-\frac{2^xcosec^2x}{\sqrt{x}}-\frac{2^xcotx}{2x^{\frac{3}{2}}}$

= $\frac{2^x}{\sqrt{x}}\left(log2cotx-cosec^2x-\frac{cotx}{2x}\right)$

Pregunta 9. Derive x ² sen x log x con respecto a x.

Solución:

Tenemos,

=> y = x ² sen x log x

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(x^2sinxlogx)$

Al usar la regla del producto, obtenemos,

= $sinxlogx\frac{d}{dx}(x^2)+x^2\frac{d}{dx}(sinxlogx)$

Al usar la regla del producto nuevamente en la segunda parte de la expresión, obtenemos,

= $sinxlogx(2x)+x^2[logx\frac{d}{dx}(sinx)+sinx\frac{d}{dx}(logx)]$

= $2xsinxlogx+x^2[logxcosx+sinx(\frac{1}{x})]$

= $2xsinxlogx+x^2logxcosx+xsinx$

Pregunta 10. Derive x ⁵ e ^x + x ⁶ log x con respecto a x.

Solución:

Tenemos,

=> y = x ⁵ e ^x + x ⁶ log x

Al diferenciar ambos lados con respecto a x, obtenemos,

$\frac{dy}{dx}=\frac{d}{dx}(x^5e^x+x^6log x)$

Al usar la regla de la string, obtenemos,

= $\frac{d}{dx}(x^5e^x)+\frac{d}{dx}(x^6log x)$

Al usar la regla del producto, obtenemos,

= $e^x\frac{d}{dx}(x^5)+x^5\frac{d}{dx}(e^x)+logx\frac{d}{dx}(x^6)+x^6\frac{d}{dx}(logx)$

= $e^x(5x^4)+x^5(e^x)+logx(6x^5)+x^6(\frac{1}{x})$

= $5x^4e^x+x^5e^x+6x^5logx+x^5$

= $x^4(5e^x+xe^x+6xlogx+x)$

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 30 Derivados – Ejercicio 30.4 | Serie 1

Pregunta 1. Derive x ³ sen x con respecto a x.

Pregunta 2. Diferenciar x ³ e ^x con respecto a x.

Pregunta 3. Derive x ² e ^x log x con respecto a x.

Pregunta 4. Diferenciar x ⁿ tan x con respecto a x.

Pregunta 5. Derive x ⁿ log _a x con respecto a x.

Pregunta 6. Diferenciar (x ³ +x ² +1)senx con respecto a x.

Pregunta 7. Diferenciar sen x cos x con respecto a x.

Pregunta 8. Diferenciar $\frac{2^xcotx}{\sqrt{x}}$ con respecto a x.

Pregunta 9. Derive x ² sen x log x con respecto a x.

Pregunta 10. Derive x ⁵ e ^x + x ⁶ log x con respecto a x.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Derive x 3 sen x con respecto a x.

Pregunta 2. Diferenciar x 3 e x con respecto a x.

Pregunta 3. Derive x 2 e x log x con respecto a x.

Pregunta 4. Diferenciar x n tan x con respecto a x.

Pregunta 5. Derive x n log a x con respecto a x.

Pregunta 6. Diferenciar (x 3 +x 2 +1)senx con respecto a x.

Pregunta 7. Diferenciar sen x cos x con respecto a x.

Pregunta 8. Diferenciar con respecto a x.

Pregunta 9. Derive x 2 sen x log x con respecto a x.

Pregunta 10. Derive x 5 e x + x 6 log x con respecto a x.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Derive x ³ sen x con respecto a x.

Pregunta 2. Diferenciar x ³ e ^x con respecto a x.

Pregunta 3. Derive x ² e ^x log x con respecto a x.

Pregunta 4. Diferenciar x ⁿ tan x con respecto a x.

Pregunta 5. Derive x ⁿ log _a x con respecto a x.

Pregunta 6. Diferenciar (x ³ +x ² +1)senx con respecto a x.

Pregunta 8. Diferenciar $\frac{2^xcotx}{\sqrt{x}}$ con respecto a x.

Pregunta 9. Derive x ² sen x log x con respecto a x.

Pregunta 10. Derive x ⁵ e ^x + x ⁶ log x con respecto a x.