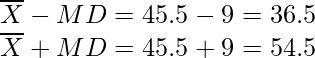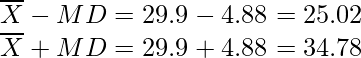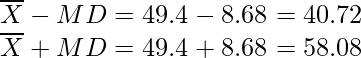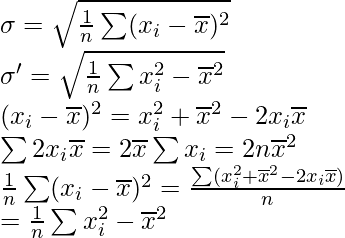Clase 11 Soluciones RD Sharma – Capítulo 32 Estadísticas – Ejercicio 32.1

Pregunta 1. Calcular la desviación media sobre la mediana de la siguiente observación:

(yo) 3011, 2780, 3020, 2354, 3541, 4150, 5000

(ii) 38, 70, 48, 34, 42, 55, 63, 46, 54, 44

(iii) 34, 66, 30, 38, 44, 50, 40, 60, 42, 51

(iv) 22, 24, 30, 27, 29, 31, 25, 28, 41, 42

(v) 38, 70, 48, 34, 63, 42, 55, 44, 53, 47

Solución:

(yo) 3011, 2780, 3020, 2354, 3541, 4150, 5000

Cálculo de la Mediana (M) de la siguiente observación:

Ordenar los números en orden ascendente,

2354, 2780, 3011, 3020, 3541, 4150, 5000

La mediana es el número medio de todas las observaciones.

Por lo tanto, Mediana = 3020 y n = 7

x _yo | _yo | = |x _i – 3020|

3011 9

2780 240

3020 0

2354 666

3541 521

4150 1130

5000 1980

Total 4546

Cálculo de la desviación media:

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

= 649,42

Por lo tanto, la desviación media es 649,42.

(ii) 38, 70, 48, 34, 42, 55, 63, 46, 54, 44

Cálculo de la Mediana (M) de la siguiente observación:

Ordenar los números en orden ascendente,

34, 38, 42, 44, 46, 48, 54, 55, 63, 70

La mediana es el número medio de todas las observaciones.

Aquí, el número de observaciones es par,

por lo tanto la Mediana = (46 + 48)/2 = 47

Mediana = 47 y n = 10

x _yo | _yo | = |x _i – 47|

38 9

70 23

48 1

34 13

42 5

55 8

63 dieciséis

46 1

54 7

44 3

Total 86

Cálculo de la desviación media:

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

= 1/10 × 86

= 8,6

Por lo tanto, la desviación media es 8,6.

(iii) 34, 66, 30, 38, 44, 50, 40, 60, 42, 51

Cálculo de la Mediana (M) de la siguiente observación:

Ordenar los números en orden ascendente,

30, 34, 38, 40, 42, 44, 50, 51, 60, 66

La mediana es el número medio de todas las observaciones.

Aquí, el número de observaciones es par,

por lo tanto la Mediana = (42 + 44)/2 = 43

Mediana = 43 y n = 10

x _yo | _yo | = |x _i – 43|

30 13

34 9

38 5

40 3

42 1

44 1

50 7

51 8

60 17

66 23

Total 87

Cálculo de la desviación media:

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

= 1/10 × 87

= 8,7

Por lo tanto, la desviación media es 8,7.

(iv) 22, 24, 30, 27, 29, 31, 25, 28, 41, 42

Cálculo de la Mediana (M) de la siguiente observación:

Ordenar los números en orden ascendente,

22, 24, 25, 27, 28, 29, 30, 31, 41, 42

La mediana es el número medio de todas las observaciones.

Aquí, el número de observaciones es par,

por lo tanto la Mediana = (28 + 29)/2 = 28.5

Mediana = 28,5 y n = 10

x _yo | _yo | = |x _i – 28,5|

22 6.5

24 4.5

30 1.5

27 1.5

29 0.5

31 2.5

25 3.5

28 0.5

41 12.5

42 13.5

Total 47

Cálculo de la desviación media:

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

= 1/10 × 47

= 4,7

Por lo tanto, la desviación media es 4,7.

(v) 38, 70, 48, 34, 63, 42, 55, 44, 53, 47

Cálculo de la Mediana (M) de la siguiente observación:

Ordenar los números en orden ascendente,

34, 38, 43, 44, 47, 48, 53, 55, 63, 70

La mediana es el número medio de todas las observaciones.

Aquí, el número de observaciones es par,

por lo tanto la Mediana = (47 + 48)/2 = 47.5

Mediana = 47,5 y n = 10

x _yo | _yo | = |x _i – 47,5|

38 9.5

70 22.5

48 0.5

34 13.5

63 15.5

42 5.5

55 7.5

44 3.5

53 5.5

47 0.5

Total 84

Cálculo de la desviación media:

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

= 1/10 × 84

= 8,4

∴ La desviación media es 8,4.

Pregunta 2. Calcule la desviación media de la media para los siguientes datos:

(yo) 4, 7, 8, 9, 10, 12, 13, 17

(ii) 13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17

(iii) 38, 70, 48, 40, 42, 55, 63, 46, 54, 44

(iv) 36, 72, 46, 42, 60, 45, 53, 46, 51, 49

(v) 57, 64, 43, 67, 49, 59, 44, 47, 61, 59

Solución:

(yo) 4, 7, 8, 9, 10, 12, 13, 17

Sabemos, desviación media,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

¿Dónde, _yo | = |x _yo – x|

Entonces, supongamos que x es la media de la observación dada.

Ahora, x = [4 + 7 + 8 + 9 + 10 + 12 + 13 + 17]/8

= 80/8

= 10

Número de observaciones, n = 8

x _yo | _yo | = |x _i – 10|

4 6

7 3

8 2

9 1

10 0

12 2

13 3

17 7

Total 24

MD = 1/8 * 24

= 3

(ii) 13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17

Ya que,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

¿Dónde, _yo | = |x _yo – x|

Entonces, supongamos que x es la media de la observación dada.

x = [13 + 17 + 16 + 14 + 11 + 13 + 10 + 16 + 11 + 18 + 12 + 17]/12

= 168/12

= 14

Número de observaciones, n = 12

x _yo | _yo | = |x _i – 14|

13 1

17 3

dieciséis 2

14 0

11 3

13 1

10 4

dieciséis 2

11 3

18 4

12 2

17 3

Total 28

Ahora,

MD = 1/12 × 28

= 2,33

(iii) 38, 70, 48, 40, 42, 55, 63, 46, 54, 44

Lo sabemos,

Desviación media, $MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

¿Dónde, _yo | = |x _yo – x|

Entonces, supongamos que x es la media de la observación dada.

x = [38 + 70 + 48 + 40 + 42 + 55 + 63 + 46 + 54 + 44]/10

= 500/10

= 50

Número de observaciones, n = 10

x _yo | _yo | = |x _i – 50|

38 12

70 20

48 2

40 10

42 8

55 5

63 13

46 4

54 4

44 6

Total 84

MD = 1/10 × 84

= 8,4

(iv) 36, 72, 46, 42, 60, 45, 53, 46, 51, 49

Desviación media,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

¿Dónde, _yo | = |x _yo – x|

Entonces, supongamos que x es la media de la observación dada.

x = [36 + 72 + 46 + 42 + 60 + 45 + 53 + 46 + 51 + 49]/10

= 500/10

= 50

Número de observaciones, n = 10

x _yo | _yo | = |x _i – 50|

36 14

72 22

46 4

42 8

60 10

45 5

53 3

46 4

51 1

49 1

Total 72

MD = 1/10 × 72

= 7,2

(v) 57, 64, 43, 67, 49, 59, 44, 47, 61, 59

Desviación media,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

¿Dónde, _yo | = |x _yo – x|

Entonces, supongamos que x es la media de la observación dada.

x = [57 + 64 + 43 + 67 + 49 + 59 + 44 + 47 + 61 + 59]/10

= 550/10

= 55

Número de observaciones, n = 10

x _yo | _yo | = |x _i – 55|

57 2

64 9

43 12

67 12

49 6

59 4

44 11

47 8

61 6

59 4

Total 74

MD = 1/10 × 74

= 7,4

Pregunta 3. Calcule la desviación media de los siguientes grupos de ingresos de cinco y siete miembros de sus medianas:

yo Ingresos en ₹	Yo Ingresos en ₹
4000	3800
4200	4000
4400	4200
4600	4400
4800	4600
	4800
	5800

Solución:

Conjunto de datos I:

Como los datos están ordenados de forma ascendente,

4000, 4200, 4400, 4600, 4800

Mediana (Mitad de la observación en orden ascendente) = 4400

Observaciones totales, n = 5

Ahora, desviación media,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

x _yo | _yo | = |x _i – 4400|

4000 400

4200 200

4400 0

4600 200

4800 400

Total 1200

MD(I) = 1/5 × 1200

= 240

Conjunto de datos II:

Como los datos están ordenados de forma ascendente,

3800, 4000, 4200, 4400, 4600, 4800, 5800

Mediana (Mitad de la observación en orden ascendente) = 4400

Observaciones totales, n = 7

Ahora, desviación media,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

x _yo | _yo | = |x _i – 4400|

3800 600

4000 400

4200 200

4400 0

4600 200

4800 400

5800 1400

Total 3200

DM(II) = 1/7 × 3200

= 457,14

Pregunta 4. Las longitudes (en cm) de 10 varillas en una tienda se dan a continuación:

40,0, 52,3, 55,2, 72,9, 52,8, 79,0, 32,5, 15,2, 27,9, 30,2

(i) Halle la desviación media de la mediana.

(ii) Encuentre también la desviación media de la media.

Solución:

(i) La desviación media de la mediana

Ordenando los datos en orden ascendente,

15,2, 27,9, 30,2, 32,5, 40,0, 52,3, 52,8, 55,2, 72,9, 79,0

Lo sabemos,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

Como el número de observaciones es par,

por lo tanto Mediana = (40 + 52,3)/2 = 46,15

Mediana = 46,15

Además, número de observaciones, n = 10

x _yo | _yo | = |x _i – 46,15|

40,0 6.15

52.3 6.15

55.2 9.05

72,9 26.75

52.8 6.65

79.0 32.85

32.5 13.65

15.2 30.95

27,9 19.25

30.2 15.95

Total 167.4

DM = 1/10 * 167,4

=16,74

(ii) Desviación media de la media también.

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

¿Dónde, _yo | = |x _yo – x|

Entonces, supongamos que x es la media de la observación dada.

Ahora, x = [40,0 + 52,3 + 55,2 + 72,9 + 52,8 + 79,0 + 32,5 + 15,2 + 27,9 + 30,2]/10

= 458/10

= 45,8

Y, número de observaciones, n = 10

x _yo | _yo | = |x _i – 45,8|

40,0 5.8

52.3 6.5

55.2 9.4

72,9 27.1

52.8 7

79.0 33.2

32.5 13.3

15.2 30.6

27,9 17.9

30.2 15.6

Total 166.4

DM = 1/10 * 166,4

= 16,64

Pregunta 5. En la pregunta 1(iii), (iv), (v) encuentre el número de observaciones que se encuentran entre 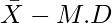$\bar{X}-M.D$ y $\bar{X}+M.D$ , donde MD es la desviación media de la media.

Solución:

(iii) 34, 66, 30, 38, 44, 50, 40, 60, 42, 51

Lo sabemos,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

¿Dónde, _yo | = |x _yo – x|

Entonces, supongamos que x es la media de la observación dada.

x = [34 + 66 + 30 + 38 + 44 + 50 + 40 + 60 + 42 + 51]/10

= 455/10

= 45,5

Y, número de observaciones, n = 10

x _yo | _yo | = |x _i – 45,5|

34 11.5

66 20.5

30 15.5

38 7.5

44 1.5

50 4.5

40 5.5

60 14.5

42 3.5

51 5.5

Total 90

MD = 1/10 × 90

= 9

Ahora,

$\overline{X}-M D = 45.5 - 9 = 36.5 \\ \overline{X}+MD = 45.5 + 9 = 54.5$

Entonces, hay un total de 6 observaciones entre $\overline{X}-MD$ y $\overline{X}+MD$

(iv) 22, 24, 30, 27, 29, 31, 25, 28, 41, 42

Lo sabemos,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

¿Dónde, _yo | = |x _yo – x|

Entonces, supongamos que x es la media de la observación dada.

x = [22 + 24 + 30 + 27 + 29 + 31 + 25 + 28 + 41 + 42]/10

= 299/10

= 29,9

Además, número de observaciones, n = 10

x _yo | _yo | = |x _i – 29,9|

22 7.9

24 5.9

30 0.1

27 2.9

29 0.9

31 1.1

25 4.9

28 1.9

41 11.1

42 12.1

Total 48.8

DM = 1/10 × 48,8

= 4,88

Y,

$\overline{X}-M D = 29.9 - 4.88 = 25.02 \\ \overline{X}+MD = 29.9 + 4.88 = 34.78$

Entonces, hay 5 observaciones en el medio.

(v) 38, 70, 48, 34, 63, 42, 55, 44, 53, 47

Lo sabemos,

$MD = \frac{1}{n}\sum_{i=1}^{n}|d_i|$

¿Dónde, _yo | = |x _yo – x|

Entonces, supongamos que x es la media de la observación dada.

x = [38 + 70 + 48 + 34 + 63 + 42 + 55 + 44 + 53 + 47]/10

= 494/10

= 49,4

Número de observaciones, n = 10

x _yo | _yo | = |x _i – 49,4|

38 11.4

70 20.6

48 1.4

34 15.4

63 13.6

42 7.4

55 5.6

44 5.4

53 3.6

47 2.4

Total 86.8

MD = = 1/10 × 86.8

= 8.68

Also,

$\overline{X}-M D = 49.4 - 8.68 = 40.72 \\ \overline{X}+MD = 49.4 + 8.68 = 58.08$

There are 6 observations in between.

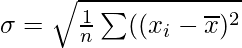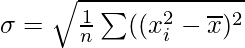Pregunta 6. Muestre que las dos fórmulas para la desviación estándar de los datos no agrupados $\sigma = \sqrt{\frac{1}{n}\sum((x_i-\overline x)^{2}}$ y $\sigma = \sqrt{\frac{1}{n}\sum((x_i^2 -\overline x)^{2}}$ son equivalentes, donde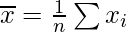 $\overline x = \frac{1}{n}\sum x_i$

Solución:

$\sigma = \sqrt{\frac{1}{n}\sum(x_i - \overline x)^2} \\ \sigma' = \sqrt{\frac{1}{n}\sum x_i^2 - \overline x^2} \\ (x_i - \overline x)^2 = x_i^2 + \overline x^2 - 2x_i\overline x \\ \sum 2x_i\overline x = 2\overline x\sum x_i = 2n\overline x^2 \\ \frac{1}{n}\sum(x_i - \overline x)^2 = \frac{\sum(x_i^2+\overline x^2-2x_i\overline x)}{n} \\= \frac{1}{n} \sum x_i^2 - \overline x^2$

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Calcular la desviación media sobre la mediana de la siguiente observación:

(yo) 3011, 2780, 3020, 2354, 3541, 4150, 5000

(ii) 38, 70, 48, 34, 42, 55, 63, 46, 54, 44

(iii) 34, 66, 30, 38, 44, 50, 40, 60, 42, 51

(iv) 22, 24, 30, 27, 29, 31, 25, 28, 41, 42

(v) 38, 70, 48, 34, 63, 42, 55, 44, 53, 47

Pregunta 2. Calcule la desviación media de la media para los siguientes datos:

(yo) 4, 7, 8, 9, 10, 12, 13, 17

(ii) 13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17

(iii) 38, 70, 48, 40, 42, 55, 63, 46, 54, 44

(iv) 36, 72, 46, 42, 60, 45, 53, 46, 51, 49

(v) 57, 64, 43, 67, 49, 59, 44, 47, 61, 59

Pregunta 3. Calcule la desviación media de los siguientes grupos de ingresos de cinco y siete miembros de sus medianas:

Pregunta 4. Las longitudes (en cm) de 10 varillas en una tienda se dan a continuación:

40,0, 52,3, 55,2, 72,9, 52,8, 79,0, 32,5, 15,2, 27,9, 30,2

(i) Halle la desviación media de la mediana.

(ii) Encuentre también la desviación media de la media.

Pregunta 5. En la pregunta 1(iii), (iv), (v) encuentre el número de observaciones que se encuentran entre y , donde MD es la desviación media de la media.

Pregunta 6. Muestre que las dos fórmulas para la desviación estándar de los datos no agrupados y son equivalentes, donde

Deja una respuesta Cancelar la respuesta

Pregunta 5. En la pregunta 1(iii), (iv), (v) encuentre el número de observaciones que se encuentran entre $\bar{X}-M.D$ y $\bar{X}+M.D$ , donde MD es la desviación media de la media.

Pregunta 6. Muestre que las dos fórmulas para la desviación estándar de los datos no agrupados $\sigma = \sqrt{\frac{1}{n}\sum((x_i-\overline x)^{2}}$ y $\sigma = \sqrt{\frac{1}{n}\sum((x_i^2 -\overline x)^{2}}$ son equivalentes, donde $\overline x = \frac{1}{n}\sum x_i$