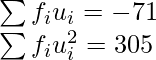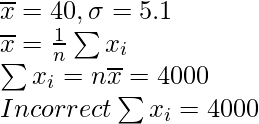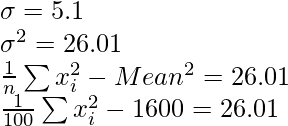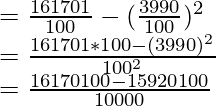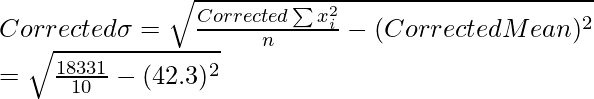Clase 11 RD Sharma Solutions – Capítulo 32 Estadísticas – Ejercicio 32.6

Pregunta 1. Calcular la media y SD para los siguientes datos:

Gasto (en ₹):	0-10	10-20	20-30	30-40	40-50
Frecuencia:	14	13	27	21	15

Solución:

CI	F	X	tu = (x – A)/h	Fu	tu ²	Fu ²
0 – 10	14	5	-2	-28	4	56
10 – 20	13	15	-1	-13	1	13
20 – 30	27	25	0	0	0	0
30 – 40	21	35	1	21	1	21
40 – 50	15	45	2	30	4	60
	90			10		150

Dado:

Número de observaciones, N = 90 y A = 25

$\sum f_iu_i =10\\ \sum f_iu_i^2 =150$

h = 10

Media = $\overline{x} = A+h(\frac{1}{N}\sum f_iu_i)$

$\overline{x}$ = 25 + 10(10/90) = 26,11

$var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]$

= 10[(150/90) – (10/90) ² ]

= 165,4

Desviación estándar = √var(x) = √165,4 = 12,86

Pregunta 2. Calcula la desviación estándar de los siguientes datos:

Clase:	0-30	30-60	60-90	90-120	120-150	150-180	180-210
Frecuencia:	9	17	43	82	81	44	24

Solución:

CI	F	X	tu = (x – A)/h	f × tu	tu ²	Fu ²
0 – 30	9	15	-3	-27	9	81
30 – 60	17	45	-2	-34	4	68
60 – 90	43	75	-1	-43	1	43
90 – 120	82	105	0	0	0	0
120 – 150	81	135	1	81	1	81
150 – 180	44	165	2	88	4	176
180 – 210	24	195	3	72	9	216
	300			137		665

Dado: N = 300 y A = 105

$\sum f_iu_i =137\\ \sum f_iu_i^2 =665$

h = 30

Media = $\overline{x} = A+h(\frac{1}{N}\sum f_iu_i)$

$\overline{x}$ = 105 + 30(137/300) = 118,7

$var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]$

= 900[(665/300) – (137/300) ² ]

= 1807.31

Desviación Estándar = √var(x) = √1807.31 = 42.51

Pregunta 3. Calcula el AM y el SD para la siguiente distribución:

Clase:	0-10	10-20	20-30	30-40	40-50	50-60	60-70	70-80
Frecuencia:	18	dieciséis	15	12	10	5	2	1

Solución:

CI	F	X	tu = (x – A)/h	f × tu	tu ²	Fu ²
0 – 10	18	5	-3	-54	9	162
10 – 20	dieciséis	15	-2	-32	4	64
20 – 30	15	25	-1	-15	1	15
30 – 40	12	35	0	0	0	0
40 – 50	10	45	1	10	1	10
50 – 60	5	55	2	10	4	20
60 – 70	2	sesenta y cinco	3	6	9	18
70 – 80	1	75	4	4	dieciséis	dieciséis
	79			-71		305

Dado: N = 79 y A =35

$\sum f_iu_i =-71\\ \sum f_iu_i^2 =305$

h = 10

Media = $\overline{x} = A+h(\frac{1}{N}\sum f_iu_i)$

$\overline{x}$ = 35 + 10(-71/79) = 26,01

$var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]$

= 100[(305/79) – (-71/79) ² ]

= 305,30

Desviación estándar = √var(x) = √305,30 = 17,47

Pregunta 4. Un estudiante obtuvo la media y la desviación estándar de 100 observaciones como 40 y 5,1 respectivamente. Más tarde se descubrió que una observación se copió incorrectamente como 50, la cifra correcta es 40. Encuentre la media y la DE correctas

Solución:

Según la pregunta, tenemos,

n = 100 , $\overline{x} = 40 , \sigma = 5.1 \\ \overline{x} = \frac{1}{n}\sum x_i \\ \sum x_i = n\overline{x} = 4000 \\ Incorrect \sum x_i = 4000$

Y también

$\sigma = 5.1 \\ \sigma^2 = 26.01 \\ \frac{1}{n}\sum x_i^2 - Mean^2 = 26.01 \\ \frac{1}{100}\sum x_i^2 - 1600 = 26.01 \\$

$\sum x_i^2$ = 1626,01 x 100

Incorrecto $\sum x_i^2$ = 162601

Al reemplazar la observación incorrecta de 50 por 40, obtenemos,

Incorrecto $\sum x_i$ = 4000

Corregido $\sum x_i$ = 4000 – 50 + 40 = 3990

Incorrecto $\sum x_i^2$ = 162601

Corregido $\sum x_i^2$ = 162601 – 50 ² + 40 ² = 161701

Ahora tenemos,

Media corregida = 39,90

Varianza corregida = (1/100)(corregida $\sum x_i^2$ ) – (media corregida) ²

$= \frac{161701}{100} - (\frac{3990}{100})^2 \\ = \frac{161701 * 100 - (3990)^2}{100^2} \\ = \frac{16170100-15920100}{10000}$

= 25

Desviación estándar corregida = √25 = 5

Pregunta 5. Calcula la media, la mediana y la desviación estándar de la siguiente distribución:

Intervalo de clases	31-35	36-40	41-45	46-50	51-55	56-60	61-65	66-70
Frecuencia:	2	3	8	12	dieciséis	5	2	3

Solución:

CI	frecuencia	Valor medio	tu _yo	si _yo tu _yo	f _yo tu _yo²
31 – 35	2	33	-4	-8	32
36 – 40	3	38	-3	-9	27
41 – 45	8	43	-2	-dieciséis	32
46 – 50	12	48	-1	-12	12
51 – 55	dieciséis	53	0	0	0
56 – 60	5	58	1	5	5
61 – 65	2	63	2	4	8
66 – 70	2	68	3	6	18
	norte = 50			Total = – 30	totales = 134

Ahora, usando los valores dados, tenemos

Media = 53 + 5 x (-30/50)

= 50

Varianza = 25 x ((134/50) – (9/25)

= 58

Desviación estándar = √58

= 7,62

Pregunta 6. Encuentre la media y la varianza de la distribución de frecuencias dada a continuación:

x _yo	1 ≤ x < 3	3 ≤ x < 5	5 ≤ x < 7	7 ≤ x < 9
yo _{_}	6	4	5	1

Solución:

Los datos se pueden convertir a una distribución de frecuencia continua restando 0,5 del límite inferior y sumando 0,5 al límite superior de cada intervalo de clase.

Intervalo de clases yo _{_} x _yo tu _yo si _yo tu _yo tu _yo² f _yo tu _yo²

1 – 2 6 1.5 -4 -24 dieciséis 96

3 – 4 4 3.5 -2 -8 4 dieciséis

5 – 6 5 5.5 0 0 0 0

7 – 8 1 7.5 2 2 4 4

norte = 16 Total = -30 totales = 116

Dado: N = 16 y A = 5.5

$\sum f_iu_i =-30\\ \sum f_iu_i^2 =116$ yh=1

Media = $\overline{x} = A+h(\frac{1}{N}\sum f_iu_i)$

$\overline{x}$ = 5,5 + 1((1/6) x (-30))

= 3.625

$var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]$

= 1 [((1/16) x 116) – ((1/16) x (-30) ² ]

= 3,74

Pregunta 7. El peso del café en 70 frascos se muestra en la siguiente tabla:

Peso (en gramos)	200-201	201-202	202-203	203-204	204-205	205-206
Frecuencia	13	27	18	10	1	1

Calcule la media, la varianza y la desviación estándar.

Solución:

CI	x _yo	yo _{_}	tu _yo	si _yo tu _yo	f _yo tu _yo²
200 – 201	200.5	13	-15	-19.5	29.25
201 – 202	201.5	27	-1	-27	27
202 – 203	202.5	18	-0.5	-9	4.5
203 – 204	203.5	10	0	0	0
204 – 205	204.5	1	0.5	0.5	0.25
205 – 206	205.5	1	1	1	1
		norte = 70		Total = – 54	totales = 62

Ahora, usando los valores dados, tenemos

Media = 203,5 + 2 x (-54/70)

= 201,9

Varianza = 4 x (62/70) – (-54/70)

= 0,98

Desviación Estándar = √0.98

= 0.099

Pregunta 8. Se encontró que la media y la desviación estándar de 100 observaciones son 40 y 10 respectivamente. Si en el momento del cálculo dos observaciones se tomaron erróneamente como 30 y 70 en lugar de 3 y 27 respectivamente, encuentre la desviación estándar correcta.

Solución:

Media = 40

Desviación estándar = 10

n = 100

$\sum x_i = 40 * 100 = 4000$

Suma corregida = 4000 – 30 +70 + 3 + 27 = 3930

Media corregida = 39,3

Varianza = 100

$100 = \frac{\sum x_i^2}{100} -(40)^2$

Incorrecto \sum x_i^2 = 170000

Entonces, Corregido \sum x_i^2 = Incorrecto $\sum x_i^2$ – (Suma de cuadrados de valores incorrectos) +

(Suma de cuadrados de valores corregidos)

Corregido $\sum x_i^2$ = 170000 – (900 + 4900) + (9+729)

= 164938

$Corrected \space \sigma = \sqrt{\frac{Corrected \space \sum x_i^2}{n}-(Corrected \space Mean)^2} \\ = \sqrt{\frac{164938}{100}-(39.3)^2} \\$

= 10,24

Pregunta 9. Mientras calculaba la media y la varianza de 10 lecturas, un estudiante usó incorrectamente la lectura de 52 para la lectura correcta de 25. Obtuvo la media y la varianza como 45 y 16 respectivamente. Encuentre la media y la varianza correctas.

Solución:

Media = 45

Varianza = 16

norte = 10

$\sum x_i = 450$

Entonces, Suma corregida = 450 – 52 + 25 = 423

Media corregida = 42,3

Varianza = 16

1 $16 = \frac{\sum x_i^2}{10} -(45)^2 \\ Incorrect \sum x_i^2 = 20410$

Corregido $\sum x_i^2$ = Incorrecto $\sum x_i^2$ – (Suma de cuadrados de valores incorrectos) +

(Suma de cuadrados de valores corregidos)

Corregido $\sum x_i^2$ = 20410 – 2704 + 625 = 18331

$Corrected \space \sigma = \sqrt{\frac{Corrected \space \sum x_i^2}{n}-(Corrected \space Mean)^2} \\ = \sqrt{\frac{18331}{10}-(42.3)^2}$

= 6,62

Entonces, Varianza corregida = 6.62 * 6.62 = 43.82

Pregunta 10. Calcule la media, la varianza y la desviación estándar de la siguiente distribución de frecuencias:

Clase	0-10	10-20	20-30	30-40	40-50	50-60
Frecuencia	11	29	18	4	5	3

Solución:

CI	x _yo	yo _{_}	tu _yo	si _yo tu _yo	f _yo tu _yo²
0-10	5	11	-3	-33	99
10-20	15	29	-2	-58	116
20-30	25	18	-1	-18	18
30-40	35	4	0	0	0
40-50	45	5	1	5	5
50-60	55	3	2	6	12
		norte = 70		Total = – 98	totales = 250

Dado:

Número de observaciones, N = 70 y A = 35

$\sum f_iu_i =-98\\ \sum f_iu_i^2 =250$

h = 10

Media = $\overline{x} = A+h(\frac{1}{N}\sum f_iu_i)$

$\overline{x}$ = 35 + 10(-98/70) = -21

$var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]$

= 100[(1/70) x 250 – (1/70) x (-98) ² ]

= 161

Desviación Estándar = √var(x)

= √161

= 12,7

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Calcular la media y SD para los siguientes datos:

Pregunta 2. Calcula la desviación estándar de los siguientes datos:

Pregunta 3. Calcula el AM y el SD para la siguiente distribución:

Pregunta 4. Un estudiante obtuvo la media y la desviación estándar de 100 observaciones como 40 y 5,1 respectivamente. Más tarde se descubrió que una observación se copió incorrectamente como 50, la cifra correcta es 40. Encuentre la media y la DE correctas

Pregunta 5. Calcula la media, la mediana y la desviación estándar de la siguiente distribución:

Pregunta 6. Encuentre la media y la varianza de la distribución de frecuencias dada a continuación:

Pregunta 7. El peso del café en 70 frascos se muestra en la siguiente tabla:

Calcule la media, la varianza y la desviación estándar.

Pregunta 8. Se encontró que la media y la desviación estándar de 100 observaciones son 40 y 10 respectivamente. Si en el momento del cálculo dos observaciones se tomaron erróneamente como 30 y 70 en lugar de 3 y 27 respectivamente, encuentre la desviación estándar correcta.

Pregunta 9. Mientras calculaba la media y la varianza de 10 lecturas, un estudiante usó incorrectamente la lectura de 52 para la lectura correcta de 25. Obtuvo la media y la varianza como 45 y 16 respectivamente. Encuentre la media y la varianza correctas.

Pregunta 10. Calcule la media, la varianza y la desviación estándar de la siguiente distribución de frecuencias:

Deja una respuesta Cancelar la respuesta