Pregunta 1. Dos plantas A y B de una fábrica muestran los siguientes resultados sobre el número de trabajadores y los salarios que se les pagan
|
|
Planta A |
Planta B |
| Nº de trabajadores |
5000 |
6000 |
| Salario promedio mensual |
$2500 |
$2500 |
| La varianza de la distribución de los salarios. |
81 |
100 |
¿En qué planta A o B hay mayor variabilidad en los salarios individuales?
Solución:
Variación de la distribución de salarios en la planta A (σ 2 =18)
Entonces, Desviación estándar de la distribución A (σ – 9)
De igual forma, la Variación de la distribución de salarios en la planta B (σ 2 =100)
Entonces, Desviación estándar de la distribución B (σ – 10)
Y, el salario promedio mensual en ambas plantas es de 2500,
Ya que, la planta con mayor valor de SD tendrá mayor variabilidad en salario.
∴ La planta B tiene más variabilidad en los salarios individuales que la planta A
Pregunta 2. Las medias y las desviaciones estándar de las alturas y los pesos de 50 estudiantes en una clase son las siguientes:
|
|
Pesos |
alturas |
| Significar |
63,2 kg |
63,2 pulgadas |
|
Desviación Estándar |
5,6 kg |
11,5 pulgadas |
¿Cuál muestra más variabilidad, alturas o pesos?
Solución:
Observamos que el peso y la altura promedio de los 50 estudiantes es el mismo, es decir, 63,2.
Por tanto, el parámetro con mayor varianza tendrá más variabilidad.
Así, la altura tiene mayor variabilidad.
Pregunta 3. Los coeficientes de variación de dos distribuciones son 60% y 70%, y sus desviaciones estándar son 21 y 16 respectivamente. ¿Cuál es su media aritmética?
Solución:
Coeficiente de variación =
Entonces tenemos:
∴ Las medias son 35 y 22,85
Pregunta 4. Calcula el coeficiente de variación a partir de los siguientes datos:
| Ingresos (en ₹): |
1000 – 1700 |
1700 – 2400 |
2400 – 3100 |
3100 – 3800 |
3800 – 4500 |
4500 – 5200 |
|
Nº de familias: |
12 |
18 |
20 |
25 |
35 |
10 |
Solución:
Clase
yo _
x yo
si yo tu yo
f yo tu yo 2
1000 – 1700
12
1350
-2
-24
48
1700 – 2400
18
2050
-1
-18
18
2400 – 3100
20
2750
0
0
0
3100 – 3800
25
3450
1
25
25
3800 – 4500
35
4150
2
70
140
4500 – 5200
10
4850
3
30
90
Ahora,
norte = 120,
Significar,
Varianza = 1076332.64
Desviación Estándar,
Coeficiente de variación =
= 32,08
∴ El coeficiente de variación es 32.08
Pregunta 5. Un análisis de los salarios semanales pagados a los trabajadores en dos empresas A y B, pertenecientes a la misma industria da los siguientes resultados:
|
Empresa A |
Empresa B |
|
| Nº de asalariados |
586 |
648 |
| Salario promedio semanal |
$52.5 |
$47.5 |
| La varianza de la distribución de los salarios. |
100 |
121 |
(i) ¿Qué empresa A o B paga la mayor cantidad como salarios semanales?
(ii) ¿Qué empresa A o B tiene mayor variabilidad en los salarios individuales?
Solución:
(i) Salario promedio semanal =
Total de salarios semanales = (Promedio de salarios semanales) × (No. de trabajadores)
Salarios semanales totales de la empresa A = 52,5 × 586 = Rs 30765
Salarios semanales totales de la empresa B = 47,5 × 648 = Rs 30780
La empresa B paga una cantidad mayor que la empresa A
(ii) Aquí,
SD (Empresa A) = 10 y SD (Empresa B) = 11
Coeficiente de varianza (Empresa A) =
= 19,04
Coeficiente de varianza (Empresa B) =
= 23,15
∴ El coeficiente de varianza de la empresa B es mayor que el de la empresa A, la empresa B tiene una mayor variabilidad en los salarios individuales.
Pregunta 6. Los siguientes son algunos detalles de la distribución de pesos de niños y niñas en una clase:
| Niños | Muchachas | |
| Número | 100 | 50 |
| Peso medio | 60 kg | 45 kg |
| Diferencia | 9 | 4 |
¿Cuál de las distribuciones es más variable?
Solución:
Dado:
SD (niños) es 3 y SD (niñas) es 2
Coeficiente de varianza (Niños) =
= 5
Coeficiente de varianza (Chicas) =
= 4,4
∴ El coeficiente de varianza de los niños es mayor que el coeficiente de varianza de las niñas, y luego la distribución de pesos de los niños es más variable que la de las niñas.
Pregunta 7. La media y la desviación estándar de las notas obtenidas por 50 estudiantes de una clase en tres materias, matemáticas, física y química se dan a continuación:
|
Tema Significar |
Matemáticas 42 |
Física 32 |
Química 40,9 |
| Desviación Estándar |
12 |
15 |
20 |
Solución:
Para comparar la variabilidad de notas en Matemáticas, Física y Química.
Tenemos que calcular su coeficiente de variación.
Sean σ 1 , σ 2 y σ 3 la desviación estándar de las notas en Matemáticas, Física y Química respectivamente. Además,
sean las puntuaciones medias en Matemáticas, Física y Química respectivamente.
Tenemos
⇒ σ 1 = 12 σ 2 = 15 σ 3 = 20
Ahora,
Coeficiente de variación en Matemáticas =
Coeficiente de variación en Física =
Coeficiente de variación en Química =
Claramente, el coeficiente de variación en las calificaciones es mayor en Química y menor en Matemáticas.
Por lo tanto, las calificaciones en química muestran la mayor variabilidad y las calificaciones en matemáticas muestran la menor variabilidad.
Pregunta 8. A partir de los datos proporcionados a continuación, indique qué grupo es más variable, G 1 o G 2 ?
|
Marcas Grupo G 1 |
10 – 20 9 |
20 – 30 30 – 40 17 32 |
40 – 50 33 |
50 – 60 60 – 70 40 10 |
70 – 80 9 |
| Grupo G 2 | 10 | 20 30 | 25 | 43 15 | 7 |
Solución:
Primero encontremos el coeficiente de la variable para el grupo G 1
CIf
10 – 20 9
20 – 30 17
xu=(x – A)/h
15 -3
25 -2
fu tu 2
-27 9
-34 4
Fu 2
81
68
30 – 40 32
40 – 50 33
35 -1
45 0
-32 1
0 0
32
0
50 – 60 40 55 1 40 1 40 60 – 70 10
70 – 80 9
65 2
75 3
20 4
27 9
40
81
150 -6 342 Aquí, N = 150, A = 45
y h = 10
∴ Media =
Coeficiente de variación =
Ahora, encontremos el coeficiente de la variable para el grupo G 2
CIf
10 – 20 10
20 – 30 20
xu=(x – A)/h
15 -3
25 -2
fu tu 2
-30 9
-40 4
Fu 2
90
80
30 – 40 30
40 – 50 25
35 -1
45 0
-30 1
0 0
30
0
50 – 60 43 55 1 43 1 43 60 – 70 15
70 – 80 7
65 2
75 3
30 4
21 9
60
63
150 -6 366 Aquí, N = 150, A = 45
y h = 10
∴ Media =
Coeficiente de variación =
El grupo G 2 es más variable
Pregunta 9. Encuentra el coeficiente de variación para los siguientes datos:
| Tamaño (en cm): 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 | 30 – 35 | 35 – 40 |
| Nº de artículos: 2 | 8 | 20 | 35 | 20 | 15 |
Solución:
CI f x
10 – 15 2 12,5
15 – 20 8 17,5
u=(x – A)/h fu u 2
-2 -4 4
-1 -8 1
Fu 2
8
8
20 – 25 20 22,5
25 – 30 35 27,5
0 0 0
1 35 1
0
35
30 – 35 20 32,5 2 40 4 80 35 – 40 15 37,5 3 45 9 135 100 108 266 Aquí, N = 100, A = 22,5
y h = 5
∴ Media =
Coeficiente de variación =
Pregunta 10. A partir de los precios de las acciones X e Y que figuran a continuación: averigüe cuál tiene un valor más estable:
| X: | 35 | 54 | 52 | 53 | 56 | 58 | 52 | 50 | 51 | 49 |
| Y: | 108 | 107 | 105 | 105 | 106 | 107 | 104 | 103 | 104 | 101 |
Solución:
x d = (x – Media)
35 -13
24 -24
re 2
169
576
52 4
53 5
dieciséis
25
56 8 64 58 10
52 4
100
dieciséis
50 2 4 51 3 9 49 1 1 480 980 ∴ Media =
Coeficiente de variación =
x d = (x – Media)
35 -13
24 -24
re 2
169
576
52 4
53 5
dieciséis
25
56 8 64 58 10
52 4
100
dieciséis
50 2 4 51 3 9 49 1 1 480 980 ∴ Media =
Coeficiente de variación =
Dado que el coeficiente de variación de la acción Y es menor que el coeficiente de variación de las acciones X, son más estables.
Publicación traducida automáticamente
Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

![Rendered by QuickLaTeX.com \overline{X}=A+h\left(\frac{\sum u_if_i}{N}\right)\\ \overline{X}=2750+700\left(\frac{83}{120}\right)\\ =3234.17\\ Var(X)=h^2\left[\frac{1}{N}\displaystyle\sum_{i=1}^nf_iu_i^2-\left(\frac{1}{N}\sum_{i=1}^nu_if_i\right)^2\right]\\ Var(X)=490000\left[\left(\frac{321}{120}\right)-\left(\frac{83}{120}\right)^2\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-60df97b80025898b88c3abf06c24d3dc_l3.png)
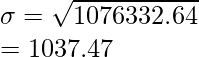
![Rendered by QuickLaTeX.com \overline{x}=A+h\left(\frac{1}{N}\sum f_iu_i\right)\\ \overline{x}=45+10\left(\frac{-6}{150}\right)=44.6\\ Var(x)=h^2\left[\frac{1}{N}\sum f_iu_i^2-\left(\frac{1}{N}\sum f_iu_i\right)^2\right]=100\left[\frac{342}{150}-\left(\frac{-6}{150}\right)^2\right]=227.84\\ S.D.=\sqrt{Var(x)}=\sqrt{227.84}=15.09](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b1fc3698509a65b63b81ee059760b518_l3.png)
![Rendered by QuickLaTeX.com \overline{x}=A+h\left(\frac{1}{N}\sum f_iu_i\right)\\ \overline{x}=45+10\left(\frac{-6}{150}\right)=44.6\\ Var(x)=h^2\left[\frac{1}{N}\sum f_iu_i^2-\left(\frac{1}{N}\sum f_iu_i\right)^2\right]=100\left[\frac{366}{150}-\left(\frac{-6}{150}\right)^2\right]=243.84\\ S.D.=\sqrt{Var(x)}=\sqrt{243.84}=15.62](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e18b459fab2af7e2ebd410714144903b_l3.png)
![Rendered by QuickLaTeX.com \overline{x}=A+h\left(\frac{1}{N}\sum f_iu_i\right)\\ \overline{x}=22.5+5\left(\frac{108}{100}\right)=27.90\\ Var(x)=h^2\left[\frac{1}{N}\sum f_iu_i^2-\left(\frac{1}{N}\sum f_iu_i\right)^2\right]=25\left[\frac{266}{100}-\left(\frac{108}{100}\right)^2\right]=37.34\\ S.D.=\sqrt{Var(x)}=\sqrt{37.34}=6.11](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2a0fa8462c41794aecafd2e42f534bf8_l3.png)
![Rendered by QuickLaTeX.com \overline{x}=\frac{1}{n}\sum x_i=\frac{1}{10}[480]=48\\ Var(x)=\frac{1}{n}\left\{\sum (x_i-\overline{x})^2\right\}=\frac{1}{10}(980)=98\\ S.D(x)=\sqrt{Var(x)}=\sqrt{98}=9.9](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05ef0de6709e01c1c66ec7d31ceea1dc_l3.png)
![Rendered by QuickLaTeX.com \overline{x}=\frac{1}{n}\sum x_i=\frac{1}{10}[1050]=105\\ Var(x)=\frac{1}{n}\left\{\sum (x_i-\overline{x})^2\right\}=\frac{1}{10}(40)=4\\ S.D(x)=\sqrt{Var(x)}=\sqrt{4}=2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e2002196f6bc7a8348f2070393934348_l3.png)