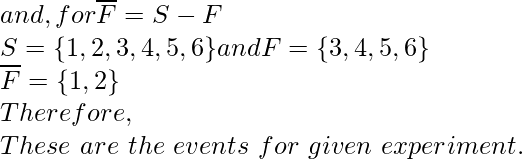Pregunta 1: Se lanza una moneda. Encuentre el número total de eventos elementales y también el número total de eventos asociados con el experimento aleatorio.
Solución:
Dado:
Se lanza una moneda.
Cuando se lanza una moneda, habrá dos resultados posibles, es decir, cara (H) y cruz (T).
Dado que el número de eventos elementales es 2-{H, T}
como sabemos que, si hay ‘n’ elementos en un conjunto, entonces el número total de elementos en su subconjunto es 2n.
Entonces, el número total del experimento es 4,
Hay 4 subconjuntos de S = {H}, {T}, {H, T} y �
Por lo tanto,
Hay un total de 4 eventos en un experimento dado.
Pregunta 2: Enumere todos los eventos asociados con el experimento aleatorio de lanzar dos monedas. ¿Cuántos de ellos son eventos elementales?
Solución:
Dado:
Se lanzan dos monedas una vez.
Como sabemos, cuando se lanzan dos monedas, el número de resultados posibles es 2 2 = 4
Asi que,
Los espacios muestrales son {HH, HT, TT, TH}
Por lo tanto,
Hay un total de 4 eventos asociados con el experimento dado.
Pregunta 3: Se lanzan tres monedas una vez. Describa los siguientes eventos asociados con este experimento aleatorio:
A = Obtener tres caras, B = Obtener dos caras y una cruz, C = Obtener tres cruces, D = Obtener una cara en la primera moneda.
(i) ¿Qué pares de eventos son mutuamente excluyentes?
(ii) ¿Qué eventos son eventos elementales?
(iii) ¿Qué eventos son eventos compuestos?
Solución:
Dado:
Hay tres monedas lanzadas una vez.
Cuando se lanzan tres monedas, los espacios muestrales son:
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Entonces, como dice la pregunta,
A = {HHH}
B = {HHT, HTH, THH}
C = {TTT}
D = {HHH, HHT, HTH, HTT}
Ahora,
A⋂ B = �,
A ⋂ C = �,
UN ⋂ RE = {HHH}
B ⋂ C = �,
segundo ⋂ re = {HHT, HTH}
do ⋂ re = �
Como sabemos, si la intersección de dos conjuntos es nula o vacía, significa que ambos conjuntos son mutuamente excluyentes.
(i) Los eventos A y B, los eventos A y C, los eventos B y C y los eventos C y D son mutuamente excluyentes.
(ii) Ahora, como sabemos que, si un evento tiene solo un punto muestral de un espacio muestral, entonces se llama eventos elementales.
Por lo tanto, A y C son eventos elementales.
(iii) Si hay un evento que tiene más de un punto muestral de un espacio muestral, se le llama evento compuesto.
Ya que, B ⋂ D = {HHT, HTH}
Por lo tanto, B y D son eventos compuestos.
Pregunta 4: En un solo lanzamiento de un dado describe los siguientes eventos:
(i) A = Obtener un número menor que 7
(ii) B = Obtener un número mayor que 7
(iii) C = Obtener un múltiplo de 3
(iv) D = Obtener un número menor que 4
(v) E = Obtener un número par mayor que 4.
(vi) F = Obtener un número no menor a 3.
Además, encuentre A ∪ B, A ∩ B, B ∩ C, E ∩ F, D ∩ F y
*** QuickLaTeX cannot compile formula: *** Error message: Error: Nothing to show, formula is empty
Solución:
Dado:
Se lanza un dado una vez.
Ahora, encuentre los eventos dados, y también encuentre A ∪ B, A ∩ B, B ∩ C, E ∩ F, D ∩ F y
S = {1, 2, 3, 4, 5, 6}
De acuerdo a la pregunta, tenemos ciertos eventos como:
(i) A = Obtener un número por debajo de 7
Por lo tanto, los espacios muestrales para A son:
A = {1, 2, 3, 4, 5, 6}
(ii) B = Obtener un número mayor que 7
Así, los espacios muestrales para B son:
B = {e}
(iii) C = Obtener múltiplo de 3
Por lo tanto, el espacio muestral de C es
C = {3, 6}
(iv) D = Obtener un número menor que 4
Por lo tanto, el espacio muestral para D es
re = {1, 2, 3}
(v) E = Obtener un número par mayor que 4.
Por lo tanto, el espacio muestral para E es
mi = {6}
(vi) F = Obtener un número no menor a 3.
Por lo tanto, el espacio muestral para F es
F = {3, 4, 5, 6}
Aquí,
A = {1, 2, 3, 4, 5, 6} y B = {¬}
UN ⋃ segundo = {1, 2, 3, 4, 5, 6}
A = {1, 2, 3, 4, 5, 6} y B = {¬}
A ⋂ B = {듓}
B = {¬} y C = {3, 6}
si ⋂ do = {¬}
F = {3, 4, 5, 6} y E = {6}
mi ⋂ F = {6}
E = {6} y D = {1, 2, 3}
RE ⋂ F = {3}
Pregunta 5: Se lanzan tres monedas. Describir
(i) dos eventos A y B que son mutuamente excluyentes.
(ii) tres eventos A, B y C que son mutuamente excluyentes y exhaustivos.
(iii) dos eventos A y B que no son mutuamente excluyentes.
(iv) dos eventos A y B que son mutuamente excluyentes pero no exhaustivos.
Solución:
Dado:
Se lanzan tres monedas.
Cuando se lanzan tres monedas, los espacios muestrales son
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Aquí,
(i) Los dos eventos que son mutuamente excluyentes son cuando,
A: sin colas
B: sin sacar cara
Después,
A = {HHH} y B = {TTT}
Entonces, la intersección de este conjunto será nula. O bien, los conjuntos son disjuntos.
(ii) Tres eventos que son mutuamente excluyentes y exhaustivos son:
A: sin sacar cara
B: sacar exactamente una cara
C: obteniendo al menos dos caras
De este modo,
A = {TTT}
B = {TTH, THT, HTT} y,
C = {HHH, HHT, HTH, THH}
Por eso,
UN ⋃ segundo = segundo ⋂ C = C ⋂ UN = � y
A⋃ B⋃ C = S
(iii) Los dos eventos que no son mutuamente excluyentes son:
A: sacando tres caras
B: obtener al menos 2 caras
Asi que,
A = {HHH}
B = {HHH, HHT, HTH, THH}
Por lo tanto, A ⋂ B = {HHH} = �
(iv) Los dos eventos que son mutuamente excluyentes pero no exhaustivos son:
A: sacar exactamente una cara
B: obtener exactamente una cola
Asi que,
A = {HTT, THT, TTH} y B = {HHT, HTH, THH}
Es porque A ⋂ B = � pero A⋃ B ≠ S
Pregunta 6: Se lanza un dado dos veces. Cada vez que se registra el número que aparece en él. Describa los siguientes eventos:
(i) A = Ambos números son impares.
(ii) B = Ambos números son pares
(iii) C = la suma de los números es menor que 6.
Además, encuentra A ∪ B, A ∩ B, A ∪ C, A ∩ C. ¿Qué pares de eventos son mutuamente excluyentes?
Solución:
Dado:
Se lanza un dado dos veces. Cada número de tiempo que aparece en él se registra.
Cuando se lanza un dado dos veces, el número de espacios muestrales es 6 2 = 36
Aquí,
La posibilidad de que ambos números impares sean:
A = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3) , (5, 5)}
Por lo tanto, la posibilidad de ambos números pares es:
B = {(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4) , (6, 6)}
Y, el posible resultado de la suma de los números es menor que 6.
C = {(1, 1)(1, 2)(1, 3)(1, 4)(2, 1)(2, 2)(2, 3)(3, 1)(3, 2)(4) , 1)}
Por eso,
(A�B) = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5) (2, 2)(2, 4)(2, 6)(4, 2)(4, 4)(4, 6)(6, 2)(6, 4)(6) , 6)}
(A y B) = {e}
(AUC) = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5) (1, 2)(1, 4)(2, 1)(2, 2)(2, 3)(3, 1)(3, 2)(4, 1)}
(AC) = {(1, 1), (1, 3), (3, 1)}
Por lo tanto,
(A�B) = � y (A�C) ≠ �, A y B son mutuamente excluyentes, pero A y C no lo son.
Pregunta 7: Se lanzan dos dados. los eventos A, B, C, D, E y F se describen a continuación:
A=Obtener un número par en el primer dado.
B=Obtener un número impar en el primer dado.
C=Obtener como máximo 5 como suma del número de los dos dados.
D=Obtener la suma de los números en los dados mayor que 5 pero menor que 10.
E=Obtener al menos 10 como la suma de los números en los dados.
F=Obtener un número impar en uno de los dados.
(i) Describa los siguientes eventos:
A y B, B o C, B y C, A y E, A o F, A y F
(ii) Indique verdadero o falso:
(a) A y B son mutuamente excluyentes
(b) A y B son eventos mutuamente excluyentes y exhaustivos.
(c) A y C son eventos mutuamente excluyentes.
(d) C y D son eventos mutuamente excluyentes y exhaustivos.
(e) C, D y E son eventos mutuamente excluyentes y exhaustivos.
(f) A’ y B’ son eventos mutuamente excluyentes.
(g) A, B, F son eventos mutuamente excluyentes y exhaustivos.
Solución:
A = Obtener un número par en el primer dado.
A = {(2, 1), (2, 2) (2, 3), (2, 4), (2, 5), (2, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
B = Obtener un número impar en el primer dado.
B = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
C = Obtener como máximo 5 como suma de los números de los dos dados.
C = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1) , (3, 2), (4, 1)}
D = Obtener la suma de los números en los dados > 5 pero < 10.
D = {(1, 5) (1, 6), (2, 4), (2, 5), (2, 6), (3, 3), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (6 , 1), (6, 2), (6, 3)}
F = Obtener un número impar en uno de los dados.
F = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), (6 , 5)}
Está claro que A y B son eventos mutuamente excluyentes y A ∩ B = ∅
B ∪ C = {(1, 1), (1,2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3,3), (3, 4), (3, 6), (5, 1), (5, 2), (5, 3), (5, 5), (5, 6) , (2,1), (2,2), (2, 3), (4, 1)}
segundo ∩ do = {(1, 1), (1, 2), (1, 3), (1, 4), (3, 1), (3, 2)}
UN ∩ MI = {(4, 6), (6, 4), (6, 5), (6, 6)}
A ∪ F = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (5, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4) , (6, 5), (6, 6)
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
A ∩ F = {(2, 1), (2,3), (2,5), (4,1), (4, 3), (4, 5), (6, 1), (6, 3), (6, 5)}
(ii)
a) Cierto, A ∩ B = ∅
b) Cierto, A ∩ B = ∅ y A ∪ B = S
c) Falso, A ∩ C ≠ ∅
d) Falso, A ∩ B = ∅ y A ∪ B ≠ S
e) Cierto, C ∩ D = D ∩ E = C ∩ E = Φ y C ∪ D ∪ E = S
f) Cierto, A’ ∩ B’ = ∅
g) Falso, A ∩ F ≠ ∅
Pregunta 8: Los números 1, 2, 3 y 4 se escriben por separado en cuatro tiras de papel. Luego, las hojas se colocan en una caja y se mezclan bien. Una persona saca dos papeletas de la caja, una tras otra, sin reposición. describir los siguientes eventos:
A=Los números de la primera hoja son más grandes que los de la segunda hoja.
B = El número en el segundo papelito es mayor que 2
C=La suma de los números en los dos papelitos es 6 o 7
D=El número en la segunda hoja es el doble que en la primera hoja.
¿Qué par(es) de eventos es (son) mutuamente excluyentes?
Solución:
Tenemos cuatro tiras de papel con los números 1, 2, 3 y 4.
Una persona saca dos papeletas sin reposición.
∴ Número de eventos elementales = 4 C 2
A = El número de la primera hoja es mayor que el de la segunda hoja
A = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}
B = El número en el segundo papelito es mayor que 2
Por lo tanto,
B = {(1,3), (2,3), (1,4), (2, 4), (3, 4), (4,3)}
C = La suma de los números en los dos papelitos es 6 o 7
Por lo tanto,
C = {(2, 4), (3, 4), (4, 2), (4, 3)}
y,
D = El número en la segunda hoja es el doble que en la primera hoja
re = {(1, 2), (2, 4)}
y, A y D forman un par de eventos mutuamente excluyentes como A ∩ B = ∅
Pregunta 9: Se toma una carta de una baraja de 52 cartas.
(i) ¿Cuál es el espacio muestral del experimento?
(ii) ¿Cuál es el evento de que la carta elegida sea una carta con cara de as?
Solución:
(i) El espacio muestral para tomar una carta de un conjunto de 52 cartas es el mismo conjunto de 52 cartas.
(ii) Para que un evento de la carta elegida sea una carta de cara negra, el evento es un conjunto de jota, rey, reina de picas y tréboles,
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA