Clase 11 RD Sharma Solutions- Capítulo 33 Probabilidad – Ejercicio 33.4 | Serie 1

Pregunta 1(a). Si A y B son eventos mutuamente excluyentes asociados con un experimento aleatorio tal que P(A) = 0.4 y P(B) = 0.5, entonces averigüe:

(i) P(AUB)

(ii)

(iii)

(iv)

Solución:

A y B son eventos mutuamente excluyentes,                

Por lo tanto, P(A n B) = 0

(i) P(AUB) = P(A) + P(B) – P(A n B) -(A y B son eventos mutuamente excluyentes, por lo tanto, P(A n B) = 0)

= 0,4 + 0,5 – 0

= 0,9

(ii)

= 1-0.9

= 0,1

(iii)   = P(B) – P(A ∩ B)

= 0,5 – 0

= 0,5

(iv)  = P(A) – P(A ∩ B)

= 0,4 – 0

= 0,4

Pregunta 1(b). A y B son dos eventos tales que P(A) = 0.54, P(B) = 0.69 & P(A ∩ B) = 0.35, luego encuentre:

(i) P(AUB)

(ii)

(iii)

(iv)

Solución:

(i) P(AUB) = P(A) + P(B) – P(A ∩ B)

P(AUB) = 0,54 + 0,69 – 0,35

P(AUB) = 0,88

(ii)  = 1 – P(AUB)

= 1-0.88

= 0,12

(iii)   = P(A) – P(A ∩ B)

 = 0,54-0,35

= 0,19

(iv)  = P(B)-P(A ∩ B)

= 0,69-0,35

= 0,34

Pregunta 1 c). Completa los espacios en blanco en la siguiente tabla                         

	PENSILVANIA)	P(B)	PAG(A ∩ B)	P(AUB)
i	1/3	1/5	1/15	—
yo	0.35	—	0.25	0.6
iii	0.5	0.35	—	0.7

Solución:

(i) P(A) = 1/3

P(B) = 1/5

P(AUB) = 1/15

P(AUB) = P(A) + P(B) – P(A ∩ B)

= 7/15

(ii) P(A) = 0,35

P(A ∩ B) = 0,25

P(AUB) = 0,6

P(AUB) = P(A) + P(B) – P(A ∩ B)

0,60 = 0,35 + P(B) – 0,25

0,60 – 0,35 + 0,25 = P(B) 

P(B) = 0,50

= 0,50

(iii) P(A) = 0,5

P(B) = 0,35

P(AUB) = 0,7

P(A ∩ B) = P(A) + P(B) – P(AUB)

= 0,5 + 0,35 – 0,7

= 0,15

Pregunta 2. A y B son dos eventos asociados con un experimento aleatorio tal que, P(A) = 0.3, P(B) = 0.4, P(AUB) = 0.5. ¿Encuentra P(A ∩ B)?

Solución:

P(A) = 0,3

P(B) = 0,4

P(AUB) = 0,5

P(A ∩ B) = P(A) + P(B) -P(AUB)

= 0,3+0,4 – 0,5

= 0,2

Pregunta 3. A y B son dos eventos asociados con un experimento aleatorio tal que, P(A) = 0.5, P(B) = 0.3, P(A n B) = 0.2. Encuentre P(AUB)?

Solución:

P(A) = 0,5

P(B) = 0,3

P(AUB) = 0,2

P(AUB) = P(A) + P(B) – P(A ∩ B)

= 0,5 + 0,3 – 0,2

= 0,6

Pregunta 4. A y B son dos eventos asociados con un experimento aleatorio tal que, 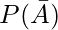  = 0.5, P(AUB) = 0.8, P(A n B) = 0.3. ¿Encuentra P(B)?

Solución:

P(A) = 1 – 

= 1 – 0,5

= 0,5

Aplicando el teorema de probabilidad de la suma:

P(AUB) = P(A) + P(B) – P(A ∩ B)

0,8 = 0,5 +P(B) – 0,3

0,8 = P(B) + 0,2

P(B) = 0,8 – 0,2

= 0,6

Pregunta 5. A y B son dos eventos mutuamente excluyentes tales que P(A) = 1/2 & P(B) = 1/3. ¿Encuentra P(A o B)?

Solución:

 A y B son dos eventos mutuamente excluyentes. 

Por lo tanto, P(A ∩ B) = 0

P(AUB) = P(A) + P(B)

= 1/2 + 1/3

= 5/6

Pregunta 6. Hay tres eventos A, B y C, uno de los cuales solo debe ocurrir. Las probabilidades son de 8 a 3 en contra de A y de 5 a 2 en contra de B, ¿encuentra impar en contra de C?

Solución:

 / P(A) = 8/3

1- P(A)/P(A) = 8/3 -(  = 1 – P(A))

P(A) = 1 + 8/3 = 3/11 -(1)

De manera similar, P(B) = 2/7 -(2)

A, B y C son eventos mutuamente excluyentes 

P(AUBUC) = P(S)

= P(A) + P(B) + P(C) = 1

= 3/11 + 2/7 + P(C) = 1

= 43/77 + P(C) = 1

= 1 – 43/77 = P(C)

= P(C) = 34/77 

=   = 1 – P(C)

= 43/77

Las probabilidades en contra de C son =

 : P(C) = 43/77 : 34/77

= 43 : 34

Pregunta 7. Uno de los dos eventos debe suceder. Dado que la probabilidad de uno es de dos tercios del otro, ¿encuentre probabilidades a favor de los demás?

Solución:

Que el azar a favor de otro sea p,

Asi que, por lo tanto

p + 2/3 p = 1

(5/3) * p = 1

pag = (3/5)

Las probabilidades a favor de otros serán:

= (2/5)/(3/5) = (3/2)

= 3 : 2

Pregunta 8. Se extrae una carta de un paquete bien barajado de 52 cartas. ¿Encuentra la probabilidad de ser espada o rey?

Solución:

Se extrae una carta de un paquete bien barajado de 52 cartas,

Por lo tanto, S(espacio muestral)= ⁵² C ₁

=52 -(1)( ⁿ C _r    = n! / (n – r)! 

                         n – número de artículos 

                         r – cuántas veces se toma un artículo)

Sea A = evento de elegir una carta de espadas

A = ¹³ C ₁           -( un juego de picas tiene 13 cartas)

= 13 -(2)

Sea B = evento de elegir un rey 

B = ⁴ C ₁           -( hay 4 reyes en el paquete de 52 cartas)

= 4 -(3)

También podemos tener un evento donde el rey dibujado es de espadas,

Por lo tanto, P(A n B) = 1 -(4)

P(AUB) = P(A) + P(B) – P(A ∩ B)

= 13/52 + 4/52 – 1/52 -(De 1, 2, 3, 4)

= 18/52

= 4/13

Pregunta 9. En una sola tirada de dos dados, ¿cuál es la probabilidad de que ni el doble ni el total sea 9?

Solución:

Se lanzan dos dados, por lo que el espacio muestral será:

S = 6 ² 

= 36 -(1)

Sea A el evento de elegir doblete: 

A = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)}

A = 6 -(2)

Sea B el evento de elegir suma igual a 9

B = {(3,6), (4,5), (5,4), (6,3)}

B = 4 -(3)

Aquí el evento A y B no pueden ocurrir juntos, es decir, la suma es 9 y los dados son dobletes.

Por lo tanto, P(A ∩ B) = 0          -(4)

Ahora,

P (AUB) = P (A) + P (B) – P (A ∩ B) – (De 1, 2, 3, 4)

= 6/36 + 4/36

= 10/36

= 5/18

Ahora, la probabilidad de que ni el doble ni el total sea 9, 

= 1 – P (AUB)

= 1 – 5/18

= 13/18

Pregunta 10. Se elige al azar un número natural de 500. ¿Cuál es la probabilidad de que un número sea divisible por 5 o por 3?

Solución:

Dado que un número se elige entre los primeros 500 números naturales, 

Por lo tanto, n(S) = 500 -(1)

Sea A el evento de elegir un número divisible por 3,

A = {3,6,9 ……………….., 498}

n(A) = 166 ( t _n  = a + (n-1) *d   

                              a = 3, d = 3, t _n = 498

                              498 = 3 + (n-1)3

                             n = 166)

PA(A) = 166/500 -(2)

Sea B el evento de elegir un número divisible por 5,

B = {5,10,15,20. . . . . .495,500}

n(B) = 100                  

P(G) = 100/500 -(3)

También podemos tener un evento donde el número es divisible por 5 y 3

P(A n B) = {15,30,45. . . . 495}

n(A n B) = 33

P(A n B) = 33/500 -(4)

Ahora,

P(AUB) = P(A) + P(B) – P(A ∩ B)

= 166/500 + 100/500 – 33/500 -(De 1, 2, 3, 4)

= 233/500

Pregunta 11. Se lanza un dado dos veces. ¿Cuál es la probabilidad de que uno de los números resulte en 3?

Solución:

Se lanzan dos dados, por lo que el espacio muestral será

n(S) = 36 -(1)

Sea A el evento de obtener 3 en el primer lanzamiento:

n(A) = 6

P(A) = 6/36

= 1/6 -(2) ((3,1), (3,2). . . (3,6))

Sea B el evento de obtener 3 en el segundo lanzamiento:

n(B) = 6

P(B) = 6/36

= 1/6 -(3)

Además, P(A ∩ B) = 1/36 -(4)(A ∩ B = (3,3))

P(AUB) = P(A) + P(B) – P(A ∩ B)

=1/6 + 1/6 – 1/36 -(De 2, 3, 4)

= 11/36

Pregunta 12. Se saca una carta de un paquete de 52 cartas. Encontrar que es de la espada o un rey?

Solución:

Hay 52 cartas, por lo que el espacio muestral será:

n(S) = 52 -(1)

Sea A el evento de obtener una carta de Picas

n(A) = 13 -( H ay 13 cartas de picas en un paquete de 52 cartas)

P(A) = 13/52

=1/4 -(2)

Sea B el evento de obtener un Rey

n(B) = 4 -( una baraja de cartas tiene 4 reyes)

P(B) = 4/52      

=1/13 -(3)

También,

P(A ∩ B) = 1/52 -(4)( A ∩ B = Un rey de picas)

P(AUB) = P(A) + P(B) – P(A ∩ B)

= 1/4 + 1/13 – 1/52 -(De 2, 3, 4)

= 4/13

Pregunta 13. La probabilidad de que un estudiante apruebe inglés e hindi es 0,5 y la probabilidad de que no apruebe ninguno es 0,1. Si la probabilidad de aprobar en inglés es 0,75, ¿cuál es la probabilidad de aprobar el examen de hindi?

Solución:

Sea E el evento de aprobar el examen de inglés –

P(E) = 0,75 -(1)

Sea H el evento de aprobar el examen de hindi:

P(H) = ?

La probabilidad de que un estudiante apruebe en inglés e hindi es 0.5,

Por lo tanto, P(E n H) = 0.5 – (2)

La probabilidad de que no pase ninguno es 0.1,

Por eso, 

 = 0,1

1 – P(EUH) = 

P(HUE) = 1 – 0,1

= 0,9 -(3)

Ahora,

P(EUH) = P(E) + P(H) – P(E ∩ H)

0,9 = 0,75 + P(H) – 0,5 -(De 1, 2, 3)

P(H) = 0,65
   

Pregunta 14. Se elige un número del 1 al 100. ¿Encuentra la probabilidad de que el número sea divisible por 4 o por 6?

Solución:

Se elige un número del 1 al 100,

Por lo tanto, el espacio muestral es – n(S) – 100

Sea A el evento de elegir un número divisible por 6;

n(A) = {6, 12, 18, 24. . . . 96}

= 25 – ( use la fórmula del término T _{n  )}

PA(A) = 25/100

= 1/4 -(1)

Sea B el evento de elegir un número divisible por 4;

n(B) = {4, 8, 12, 20. . . . 100}

= 25 – ( use la fórmula del término T n)

P (B) = 25/100

= 1/4 -(2)

Además, (A ∩ B) = {12,24,36. . . 96}

n(A ∩ B) = 8

P(A ∩ B) = 8/100 -(3)

P(AUB) = P(A) + P(B) – P(A∩ B)

= 1/4 + 1/4 – 8/100 -(De 1, 2, 3)

= 33/100