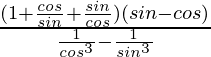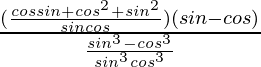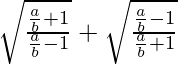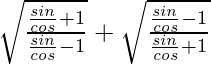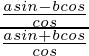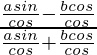Pregunta 14. Demuestra que 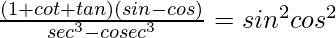
Solución:
Tenemos
Tomando LHS
=
=
=
=
=
=
= sen 2 θ cos 2 θ
Por lo tanto, LHS = RHS (Probado)
Pregunta 15. Demuestra que 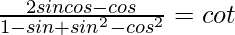
Solución:
Tenemos
Tomando LHS
=
=
=
=
=
= cosθ/senθ
= cunaθ
Por lo tanto, LHS = RHS (Probado)
Pregunta 16. Demuestra que cosθ(tanθ + 2)(2tanθ + 1) = 2secθ + 5sinθ
Solución:
Tenemos
cosθ(tanθ + 2)(2tanθ + 1) = 2secθ + 5sinθ
Tomando LHS
= cosθ(tanθ + 2)(2tanθ + 1)
=
=
=
=
=
=
= 2segθ + 5senθ
Por lo tanto, LHS = RHS (Probado)
Pregunta 17. Si x = 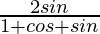 , demuestre que
, demuestre que 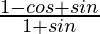 también es igual a x.
también es igual a x.
Solución:
Tenemos
x =
Tomando LHS
=
=
=
=
=
Pregunta 18. Si , entonces encuentre los valores de tanθ, secθ y cosecθ 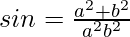
Solución:
Tenemos
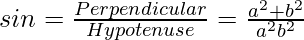
Como sabemos que
cosθ = √1 – sen 2 θ -(1)
Ahora pon el valor de sinθ en la ecuación (1)
cosθ =
=
=
=
=
Entonces el valor de cosθ =
Ahora,
tanθ =
segθ =
cosecθ =
Método alternativo:
Tenemos
Dibujamos un △PQR en ángulo recto en Q PR = a 2 + b 2 y PQ = a 2 – b 2
Por el teorema de Pitágoras, tenemos
PR 2 = PQ 2 + QR 2
QR 2 = (a 2 + b 2 ) 2 – (a 2 – b 2 ) 2
QR 2 = (un 4 + segundo 4 + 2a 2 segundo 2 ) − (un 4 + segundo 4 − 2a 2 segundo 2 )
QR 2 = 4a 2 b 2
QR = 2ab
cosθ =
Ahora,
tanθ =
segθ =
cosecθ =
Pregunta 19. Si tanθ = a/b, encuentra el valor de 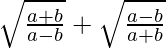
Solución:
Tenemos
=
=
Ahora pon tanθ = a/b
=
=
=
=
=
Pregunta 20. Si tanθ = a/b, demuestre que 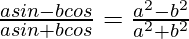 .
.
Solución:
Tenemos
Tomando LHS
=
Dividiendo denominador y numerador por cosθ
=
=
=
=
=
=
Por lo tanto, LHS = RHS (Probado)
Pregunta 21. Si cosecθ – sinθ = a 3 , secθ – cosθ = b 3 , entonces demuestre que a 2 b 2 (a 2 + b 2 ) = 1.
Solución:
Dado: cosecθ – sinθ = a 3
1/senθ − senθ = a 3
= un 3
cos 2 θ/senθ = a 3
a = (cos 2 θ/senθ) 1/3
De manera similar, b = (sen 2 θ/cosθ) 1/3
Ahora poniendo los valores de a y b en la siguiente ecuación
Tomando LHS
= un 2 segundo 2 (un 2 + segundo 2 )
= un 4 segundo 2 + un 2 segundo 4
=
= cos 6/3 θ + sen 6/3 θ
= cos 2 θ + sen 2 θ
= 1
Por lo tanto, LHS = RHS (Probado)
Pregunta 22. Si cotθ(1 + sinθ) = 4m y cotθ(1 − sinθ) = 4n, prueba que (m 2 – n 2 ) 2 = mn.
Solución:
Dado: cotθ(1 + sinθ) = 4m y cotθ(1 − sinθ) = 4n
Multiplicando ambas ecuaciones
16mn = cot 2 θ(1 – sen 2 θ)
16 minutos =
16mn = cos 4 θ/sen 2 θ
mn = cos 4 θ/16sen 2 θ -(1)
Ahora elevando al cuadrado las ecuaciones dadas
16m 2 = cot 2 θ(1 + senθ) 2 y 16n 2 = cot 2 θ(1 – senθ) 2
Al restar ambas ecuaciones, obtenemos
16m 2 – 16n 2 = cot 2 θ(1 + senθ) 2 – cot 2 θ(1 – senθ) 2
16(m 2 – n 2 ) = cot 2 θ((1 + senθ) 2 – (1 – senθ) 2 )
16(m 2 – n 2 ) =
(m 2 – n 2 ) = cos 2 θ/4sinθ
Al elevar al cuadrado ambos lados, obtenemos
(m 2 – n 2 ) 2 = cos 4 θ/16senθ -(2)
De la ecuación (1) y (2)
(m 2 – n 2 ) 2 = min
Por lo tanto probado
Pregunta 23. Si senθ + cosθ = m entonces demuestre que sen 6 θ + cos 6 θ = 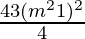 , donde m 2 ≤ 2.
, donde m 2 ≤ 2.
Solución:
Dado: senθ + cosθ = m
Al elevar al cuadrado ambos lados, obtenemos
(senθ + cosθ) 2 = m 2
= sen 2 θ + cos 2 θ + 2 sen θ cos θ = m 2
= 2senθcosθ = metro 2 − 1
Ahora,
Tomando LHS
= sen 6 θ + cos 6 θ
Usando a 3 + b 3 = (a + b)(a 2 + b 2 − ab)
= (sen 2 θ) 3 + (cos 2 θ) 3
= (sen 2 θ + cos 2 θ)(sen 4 θ + cos 4 θ − sen 2 θ cos 2 θ)
= (1)((sen 2 θ) 2 + (cos 2 θ) 2 − sen 2 θcos 2 θ)
= (sen 2 θ + cos 2 θ) 2 − 2 sen 2 θ cos 2 θ − sen 2 θ cos 2 θ
= (1 − 3sen 2 θcos 2 θ)
=
=
=
Por lo tanto, Probado.
Pregunta 24. Si a = secθ – tanθ y b = cosecθ + cotθ, entonces demuestre que ab + a – b + 1 = 0.
Solución:
Tenemos
a = secθ – tanθ y b = cosecθ + cotθ
y tenemos que demostrar que
ab + a – b + 1 = 0
Entonces, tomando LHS
ab + a – b + 1
Ahora pon los valores de a y b, obtenemos
= (secθ – tanθ)(cosecθ + cotθ) – (secθ – tanθ) + (cosecθ + cotθ) + 1
= (1/cosθ – sinθ/cosθ)(1/sinθ + cosθ/sinθ) – (1/cosθ – sinθ/cosθ) + (1/sinθ + cosθ/sinθ) + 1
= 1/cosθsinθ + 1/cosθ x cosθ/sinθ – sinθ/cosθ x 1/sinθ – (sinθ/cosθ) x (cosθ/sinθ) + 1/cosθ – sinθ/cosθ – 1/sinθ – cosθ/sinθ + 1
= 1/cosθsenθ + 1/senθ – 1/cosθ – 1 + 1/cosθ – senθ/cosθ – 1/senθ – cosθ/senθ + 1
= 1/cosθsenθ – senθ/cosθ – cosθ/senθ
= 1 – sen 2 θ – cos 2 θ/senθcosθ
= 1 – (sen 2 θ + cos 2 θ)/sen θ cos θ
= 1 – 1/senθcosθ
= 0
Por lo tanto, LHS = RHS (Probado)
Pregunta 25. 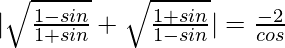 , donde π/2 < θ < π.
, donde π/2 < θ < π.
Solución:
Tenemos
Tomando LHS
=
=
=
=
=
=
=
= 2/cosθ
Dado que π/2 < θ < π , donde cosθ es negativo
Entonces, -2/cosθ
Por lo tanto, LHS = RHS (Probado)
Pregunta 26 (i). Si T n = sen n θ + cos n θ, demuestre que
\frac{T_3-T_5}{T_1}=\frac{T_5-T_7}{T_5}
Solución:
IZQ =
= sen 2 θ cos 2 θ
lado derecho =
=
= sen2θcos 2 θ
Pregunta 26 (ii). Si T n = sen n θ + cos n θ, demuestre que
2T 6 – 3T 4 + 1 = 0
Solución:
LHS = 2(sen 6 θ + cos 6 θ) – 3(sen 4 θ + cos 4 θ) + 1
Usando (a 3 + b 3 ) = (a + b)(a 2 + b 2 – ab)
= 2(sen 2 θ + cos 2 θ)(sen 4 θ + cos 4 θ – sen 2 θcos 2 θ) – 3(sen 4 θ + cos 4 θ) + 1
= 2(1)(sen 4 θ + cos 4 θ – sen 2 θ cos 2 θ) – 3(sen 4 θ + cos 4 θ) + 1
= 2sen 4 θ + 2cos 4 θ – 2sen 2 θcos 2 θ – 3sen 4 θ – 3cos 4 θ + 1
= -sen 4 θ – cos 4 θ – 2sen 2 θ cos 2 θ + 1
= -(sen 2 θ + cos 2 θ) 2 + 1
= -1 + 1 = 0 = RHS (por lo tanto probado)
Pregunta 26 (iii). Si T n = sen n θ + cos n θ, demuestre que
6T 10 – 15T 8 + 10T 6 – 1 = 0
Solución:
T 6 = sen 6 θ + cos 6 θ
Usando a 3 + b 3 = (a + b)(a 2 + b 2 − ab)
= (sen 2 x) 3 + (cos 2 x) 3
= (sen 2 x + cos 2 x)(sen 4 x + cos 4 x − sen 2 x cos 2 x)
Usando a 2 + b 2 = (a + b) 2 − 2ab
= (1)(sen 4 x + cos 4 x − sen 2 x cos 2 x)
= (sen 2 x) 2 + (cos 2 x) 2 − sen 2 x cos 2 x
= (sen 2 x + cos 2 x) 2 − 3 sen 2 x cos 2
= 1 − 3 sen 2 x cos 2 x
De manera similar, obtenemos los valores de T 8 y T 10
T 8 = (sen 6 x + cos 6 x)(sen 2 x + cos 2 x) − sen 2 x cos 2 x (sen 4 x + cos 4 x)
= 1 − 3sen 2 xcos 2 x − sen 2 xcos 2 x(1 − 2sen 2 xcos 2 x)
= 1 − 4 sen 2 x cos 2 x + 2 sen 4 x cos 4 x
T 10 = sen 10 θ + cos 10 θ
= (sen 6 θ + cos6θ)(sen 4 θ + cos 4 θ) − sen4θcos 4 θ(sen 2 θ + cos 2 θ)
= (1 − 3sen 2 xcos 2 x)(1 − 2sen 2 xcos 2 x) − sen 4 xcos 4 x
= 1 − 5 sen 2 x cos 2 x + 5 sen 4 x cos 4 x
Al poner los valores de T6, T8 y T10 en la siguiente ecuación
6T 10 – 15T 8 + 10T 6 – 1
Obtenemos el valor 0.
Por lo tanto probado
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA