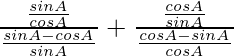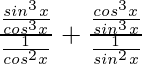Clase 11 Soluciones RD Sharma – Capítulo 5 Funciones trigonométricas – Ejercicio 5.1 | Serie 1

Posted on by Rudeus Greyrat

Demuestra las siguientes identidades (1 – 13)

Pregunta 1. sec 4 θ – sec 2 θ = tan 4 θ + tan 2 θ  

Solución:

Tenemos

segundo 4 θ – segundo 2 θ = bronceado 4 θ + bronceado 2 θ

Tomando LHS

= segundo 4 θ – segundo 2 θ

= segundo 2 θ(segundo 2 θ – 1)

Usando sec 2 θ = tan 2 θ + 1, obtenemos 

= (1 + bronceado 2 θ) bronceado 2 θ         

= tan 2 θ + tan 4 θ

Por lo tanto, LHS = RHS (Probado)

Pregunta 2. sen 6 θ + cos 6 θ = 1 – 3 sen 2 θ cos 2 θ      

Solución:

Tenemos

sen 6 θ + cos 6 θ = 1 – 3 sen 2 θ cos 2 θ 

Tomando LHS

= sen 6 θ + cos 6 θ   

= (sen 2 θ) 3 + (cos 2 θ) 3

Usando a 3 + b 3 = (a + b)(a 2 + b 2 – ab), obtenemos

= (sen 2 θ + cos 2 θ)(sen 4 θ + cos 4 θ – sen 2 θ cos 2 θ)     

Usando a 2 + b 2 = (a + b) 2 – 2ab y sin 2 θ + cos 2 θ = 1, obtenemos

= (1)[(sen 2 θ + cos 2 θ) 2 – 2sen 2 θcos 2 θ – sen 2 θcos 2 θ]             

= (1)[(1) 2 – 3sen 2 θcos 2 θ] 

= 1 – 3sen 2 θcos 2 θ

Por lo tanto, LHS = RHS (Probado)

Pregunta 3. (cosecθ – sinθ)(secθ – cosθ)(tanθ + cotθ) = 1

Solución:

Tenemos

(cosecθ – senθ)(secθ – cosθ)(tanθ + cotθ) = 1

Tomando LHS

= (cosecθ – senθ)(secθ – cosθ)(tanθ + cotθ)

Usando cosecθ = 1/sinθ y secθ = 1/cosθ   

= (\frac{1}{sinθ} - sin θ)(\frac{1}{cosθ}-cos θ)(\frac{sinθ}{cosθ}+\frac{cosθ}{sinθ})   

= (\frac{1- sin^2 θ}{sinθ} )(\frac{1- cos^2 θ}{cosθ})(\frac{sin^2θ+cos^2 θ}{cosθsinθ})   

= (\frac{cos^2 θ}{sinθ} )(\frac{sin^2θ}{cosθ})(\frac{1}{cosθsinθ})

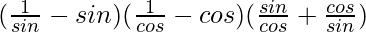
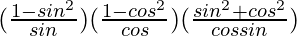
= 1

Por lo tanto, LHS = RHS (Probado)

Pregunta 4. cosecθ(secθ – 1) – cotθ(1 – cosθ) = tanθ – sinθ

Solución:

Tenemos

cosecθ(secθ – 1) – cotθ(1 – cosθ) = tanθ – sinθ

Tomando LHS

= \frac{1}{sinθ}(\frac{1}{cosθ}-1)-\frac{cosθ}{sinθ}(1-cosθ)

= \frac{1}{sinθ}(\frac{1-cosθ}{cosθ})-\frac{cosθ}{sinθ}(1-cosθ)

= \frac{(1-cosθ)}{sinθ}[(\frac{1}{cosθ})-cosθ]

= \frac{(1-cosθ)}{sinθ}(\frac{1-cos^2θ}{cosθ})

= \frac{(1-cosθ)}{sinθ}(\frac{sin^2θ}{cosθ})

= \frac{sinθ}{cosθ}-sinθ

= \frac{sinθ}{cosθ}-sinθ

Por lo tanto, LHS = RHS (Probado)

Pregunta 5. 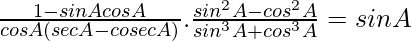\frac{1-sinAcosA}{cosA(secA-cosecA)}.\frac{sin ^2A-cos^2A}{sin^3A+cos^3A}=sinA

Solución:

Tenemos

\frac{1-sinAcosA}{cosA(secA-cosecA)}.\frac{sin ^2A-cos^2A}{sin^3A+cos^3A}=sinA

Tomando LHS

= \frac{1-sinAcosA}{cosA(\frac{1}{cosA}-\frac{1}{sinA})}.\frac{(sin A)^2-(cosA)^2}{(sinA)^3+(cosA)^3}   

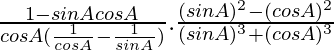
Usando a 2 – b 2 = (a + b)(a – b) y a 3 + b 3 = (a + b)(a 2 + b 2 ab), obtenemos

= \frac{1-sinAcosA}{cosA(\frac{sinA-cosA}{cosAsinA})}.\frac{(sin A+cosA)(sinA-cosA)}{(sinA+cosA)(sin^2A+cos^2A-sinAcosA)}

= \frac{sinA(1-sinAcosA)}{(sinA-cosA)}.\frac{(sin A+cosA)(sinA-cosA)}{(sinA+cosA)(sin^2A+cos^2A-sinAcosA)}

= \frac{sinA(1-sinAcosA)}{1}.\frac{1}{(sin^2A+cos^2A-sinAcosA)}

= \frac{sinA(1-sinAcosA)}{1}.\frac{1}{(1-sinAcosA)}

= senA

Por lo tanto, LHS = RHS (Probado)

Pregunta 6. 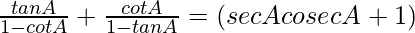\frac{tanA}{1-cotA}+\frac{cotA}{1-tanA}=(secAcosecA+1)

Solución:

Tenemos

\frac{tanA}{1-cotA}+\frac{cotA}{1-tanA}=(secAcosecA+1)

Tomando LHS

= \frac{tanA}{1-cotA}+\frac{cotA}{1-tanA}

Usando tanA = sinA/cosA y cotA = cosA/sinA, obtenemos

= \frac{\frac{sinA}{cosA}}{1-\frac{cosA}{sinA}}+\frac{\frac{cosA}{sinA}}{1-\frac{sinA}{cosA}}                             

= \frac{\frac{sinA}{cosA}}{\frac{sinA-cosA}{sinA}}+\frac{\frac{cosA}{sinA}}{\frac{cosA-sinA}{cosA}}

= \frac{sin^2A}{cosA(sinA-cosA)}-\frac{cos^2A}{sinA(sinA-cosA)}

= \frac{sin^3A-cos^3A}{sinAcosA(sinA-cosA)}

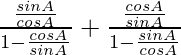
Usando a 3 – b 3 = (a – b)(a 2 + b 2 + ab), obtenemos

= \frac{(sinA-cosA)[(sinA)^2+(cosA)^2+sinAcosA]}{sinAcosA(sinA-cosA)}      

= \frac{(1+sinAcosA)}{sinAcosA}

= \frac{1}{sinAcosA}+\frac{sinAcosA}{sinAcosA}

Usando cosecA = 1/sinA y secA = 1/cosA, obtenemos

= secAcosecA + 1         

Por lo tanto, LHS = RHS (Probado)                

Pregunta 7.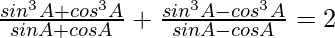 \frac{sin^3A+cos^3A}{sinA+cosA}+\frac{sin^3A-cos^3A}{sinA-cosA}=2

Solución:  

Tenemos

\frac{sin^3A+cos^3A}{sinA+cosA}+\frac{sin^3A-cos^3A}{sinA-cosA}=2

Tomando LHS

= \frac{sin^3A+cos^3A}{sinA+cosA}+\frac{sin^3A-cos^3A}{sinA-cosA}

Usando a 3 ± b 3 = (a ± b)(a 2 + b 2 ± ab), obtenemos

= \frac{(sinA+cosA)((sinA)^2+(cosA)^2-sinAcosA)}{sinA+cosA}+\frac{(sinA-cosA)((sinA)^2+(cosA)^2+sinAcosA)}{sinA-cosA}  

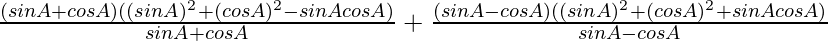
Usando sen 2 θ + cos 2 θ = 1, obtenemos

= 1 – sinAcosA + 1 + sinAcosA          

= 2

Por lo tanto, LHS = RHS (Probado)

Pregunta 8. (secAsecB + tanAtanB) 2 – (secAtanB + tanAsecB) 2 = 1

Solución:

Tenemos

(secAsecB + tanAtanB) 2 – (secAtanB + tanAsecB) 2 = 1

Tomando LHS

= (secAsecB + tanAtanB) 2 – (secAtanB + tanAsecB) 2

Expandiendo la ecuación anterior usando la fórmula  

(a + b) 2 = a 2 + b 2 + 2ab

= (secAsecB) 2 + (tanAtanB) 2 + 2(secAsecB)(tanAtanB) – 

   (secAtanB) 2 – (tanAsecB) 2 – 2(secAtanB)(tanAsecB)

= seg 2 Asec 2 B + tan 2 Atan 2 B – seg 2 Atan 2 B – tan 2 Asec 2 B

= sec 2 A(sec 2 B – tan 2 B) – tan 2 A(sec 2 B – tan 2 B)

= sec 2 A – tan 2 A -(Usando sec 2 θ – tan 2 θ = 1)

= 1

Por lo tanto, LHS = RHS (Probado)

Pregunta 9. 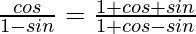\frac{cosθ}{1-sinθ}=\frac{1+cosθ+sinθ}{1+cosθ-sinθ}

Solución:

Tenemos

\frac{cosθ}{1-sinθ}=\frac{1+cosθ+sinθ}{1+cosθ-sinθ}

Tomando RHS

= \frac{1+cosθ+sinθ}{1+cosθ-sinθ}

= \frac{(1+cosθ)+sinθ}{(1+cosθ)-sinθ}

=  \frac{(1+cosθ)+sinθ}{(1+cosθ)-sinθ} ×\frac{(1+cosθ)+sinθ}{(1+cosθ)+sinθ}

= \frac{((1+cosθ)+sinθ)^2}{(1+cosθ)^2-sin^2θ}

= \frac{(1+cosθ)^2+sin^2θ+2(1+cosθ)(sinθ)}{(1)^2+(cosθ)^2+2cosθ-(sin^2θ)}

= \frac{(1)^2+(cosθ)^2+2cosθ+sin^2θ+2sinθ+2cosθsinθ}{(1)^2+(cosθ)^2+2cosθ-(sin^2θ)}

= \frac{1+cos^2θ+sin^2θ+2cosθ+2sinθ+2cosθsinθ}{(1-sin^2θ)+(cosθ)^2+2cosθ}

= \frac{1+1+2cosθ+2sinθ+2cosθsinθ}{cos^2θ+cos^2θ+2cosθ}

= \frac{2(1+cosθ+sinθ+cosθsinθ)}{2cosθ(cosθ+1)}

= \frac{(1+cosθ)+sinθ(1+cosθ)}{cosθ(cosθ+1)}

= \frac{(1+cosθ)(1+sinθ)}{cosθ(cosθ+1)}

= \frac{(1+sinθ)}{cosθ}

=  \frac{(1+sinθ)}{cosθ} ×\frac{cosθ}{cosθ}

= \frac{(1+sinθ)(cosθ)}{cos^2θ}

= \frac{(1+sinθ)(cosθ)}{1-sin^2θ}

= \frac{(1+sinθ)(cosθ)}{(1-sinθ)(1+sinθ)}

= \frac{cosθ}{(1-sinθ)}

Por lo tanto, RHS = LHS (Probado)

Pregunta 10. 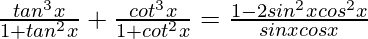\frac{tan^3x}{1+tan^2x} + \frac{cot^3x}{1+cot^2x}=\frac{1-2sin^2xcos^2x}{sinxcosx}

Solución:

Tenemos

\frac{tan^3x}{1+tan^2x} + \frac{cot^3x}{1+cot^2x}=\frac{1-2sin^2xcos^2x}{sinxcosx}

Tomando LHS

= \frac{tan^3x}{1+tan^2x} + \frac{cot^3x}{1+cot^2x}

Usando 1 + tan 2 x = sec 2 x y 1 + cot 2 x = cosec 2 x, obtenemos

= \frac{tan^3x}{sec^2x} + \frac{cot^3x}{cosec^2x}

= \frac{\frac{sin^3x}{cos^3x}}{\frac{1}{cos^2x}} + \frac{\frac{cos^3x}{sin^3x}}{\frac{1}{sin^2x}}

= \frac{sin^3x}{cosx} + \frac{cos^3x}{sinx}

= \frac{sin^4x + cos^4x}{sinxcosx}

= \frac{(sin^2x)^2 + (cos^2x)^2}{sinxcosx}

Usando a 2 + b 2 = (a + b) 2 – 2ab, obtenemos

= \frac{(sin^2x+cos^2x)^2 - 2sin^2xcos^2x}{sinxcosx}

= \frac{(1)^2-2sin^2θcos^2θ}{sinθcosθ}

= \frac{1-2sin^2xcos^2x}{sinxcosx}

Por lo tanto, LHS = RHS (Probado)

Pregunta 11. 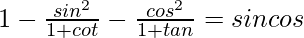1-\frac{sin^2θ}{1+cotθ}-\frac{cos^2θ}{1+tanθ}=sinθcosθ

Solución:

Tenemos

1-\frac{sin^2θ}{1+cotθ}-\frac{cos^2θ}{1+tanθ}=sinθcosθ

Tomando LHS

= 1-\frac{sin^2θ}{1+cotθ}-\frac{cos^2θ}{1+tanθ}

Usando las fórmulas cotθ = cosθ/sinθ y tanθ = sinθ/cosθ, obtenemos

= 1-\frac{sin^2θ}{1+\frac{cosθ}{sinθ}}-\frac{cos^2θ}{1+\frac{sinθ}{cosθ}}

= 1-\frac{sin^3θ}{sinθ+cosθ}-\frac{cos^3θ}{cosθ+sinθ}

= \frac{cosθ+sinθ-sin^3θ-cos^3θ}{sinθ+cosθ}

Usando a 3 +b 3 = (a + b)(a 2 + b 2 – ab), obtenemos  

= \frac{cosθ+sinθ-(sinθ+cosθ)(sin^2θ+cos^2θ-sinθcosθ)}{sinθ+cosθ}                                   

= \frac{(cosθ+sinθ)(1-sin^2θ-cos^2θ+sinθcosθ)}{(sinθ+cosθ)}

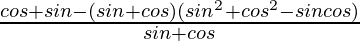
= 1 – (sen 2 θ + cos 2 θ) + sen θ cos θ

= 1 – 1 + senθcosθ

= senθcosθ

Por lo tanto, LHS = RHS (Probado)

Pregunta 12.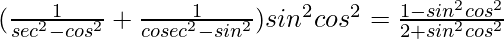(\frac{1}{sec^2θ-cos^2θ}+\frac{1}{cosec^2θ-sin^2θ})sin^2θcos^2θ=\frac{1-sin^2θcos^2θ}{2+sin^2θcos^2θ}

Solución:

Tenemos

= (\frac{1}{sec^2θ-cos^2θ}+\frac{1}{cosec^2θ-sin^2θ})sin^2θcos^2θ=\frac{1-sin^2θcos^2θ}{2+sin^2θcos^2θ}

Tomando LHS

= (\frac{1}{sec^2θ-cos^2θ}+\frac{1}{cosec^2θ-sin^2θ})sin^2θcos^2θ

= (\frac{1}{\frac{1}{cos^2θ}-cos^2θ}+\frac{1}{\frac{1}{sin^2θ}-sin^2θ})sin^2θcos^2θ      

= (\frac{cos^2θ}{1-cos^4θ}+\frac{sin^2θ}{1-sin^4θ})sin^2θcos^2θ

= (\frac{cos^2θ(1-sin^4θ)+sin^2θ(1-cos^4θ)}{(1-cos^4θ)(1-sin^4θ)})sin^2θcos^2θ

= (\frac{cos^2θ-cos^2θsin^4θ+sin^2θ-sin^2θcos^4θ)}{(1-cos^2θ)(1+cos^2θ)(1-sin^2θ)(1+sin^2θ)})sin^2θcos^2θ

= (\frac{1-cos^2θsin^4θ-sin^2θcos^4θ)}{sin^2θ(1+cos^2θ)cos^2θ(1+sin^2θ)})sin^2θcos^2θ

= (\frac{1-cos^2θsin^2θ(sin^2θ+cos^2θ)}{(1+cos^2θ)(1+sin^2θ)})

= \frac{1-cos^2θsin^2θ}{(1+cos^2θ+sin^2θ+cos^2θsin^2θ)}

= \frac{1-cos^2θsin^2θ}{2+cos^2θsin^2θ}

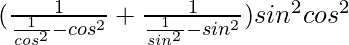
Por lo tanto, LHS = RHS (Probado)

Pregunta 13. (1 + tanαtanβ) 2 + (tanα – tanβ) 2   = sec 2 αsec 2 β

Solución:

Tenemos

(1 + tanαtanβ) 2 + (tanα – tanβ) 2 = sec^2αsec 2 β

Tomando LHS

= (1 + tanαtanβ) 2 + (tanα – tanβ) 2

= (1 + tan 2 αtan 2 β + 2tanαtanβ) + (tan 2 α + tan 2 β – 2tanαtanβ)

= 1 + bronceado 2 α bronceado 2 β + bronceado 2 α + bronceado 2 β

= (1 + tan 2 β) + tan 2 α(1 + tan 2 β)

= (1 + tan 2 β)(1 + tan 2 α)

= segundo 2 α segundo 2 β

Por lo tanto, LHS = RHS (Probado)

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *