Pregunta 1. Encuentra los valores de las otras cinco funciones trigonométricas en cada una de las siguientes:
(i) cot x = 12/5, x en el cuadrante III
(ii) cos x = -1/2, x en el cuadrante II
(iii) tan x = 3/4, x en el cuadrante III
(iv) sen x = 3/5, x en el cuadrante I
Solución:
(i) cot x = 12/5, x en el cuadrante III
Como sabíamos que tan x y cot x son positivos en el tercer cuadrante
y sen x, cos x, sec x, cosec x son negativos.
Usando las fórmulas,
bronceado x = 1/cuna x
=
= 5/12
cosec x =
= -13/5
sen x = 1/coseg x
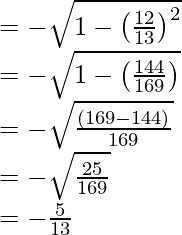
=
=- 5/13
porque x =
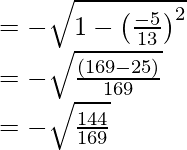
= -12/13
seg x = 1/cos x
=
= – 13/12
Por lo tanto, los valores de las otras cinco funciones trigonométricas son: sin x = -5/13, cos x = -12/13, tan x = 5/12, cosec x = -13/5, sec x = -13/12
(ii) cos x = -1/2, x en el cuadrante II
Como sabíamos que sen x y cosec x son positivos en el segundo cuadrante y
tan x, cot x, cos x, sec x son negativos.
Usando las fórmulas, obtenemos
sen x =
= -2Por lo tanto, los valores de las otras cinco funciones trigonométricas son: sin x = √3/2, tan x = -√3, cosec x = 2/√3, cot x = -1/√3, sec x = -2
(iii) tan x = 3/4, x en el cuadrante III
Como sabíamos que tan x y cot x son positivos en el tercer cuadrante y sen x, cos x, sec x, cosec x son negativos.
Usando las fórmulas,
sen x =
Por lo tanto, los valores de las otras cinco funciones trigonométricas son: sin x = -3/5, cos x = -4/5, cosec x = -5/3, sec x = -5/4, cot x = 4/3
(iv) sen x = 3/5, x en el cuadrante I
Como sabíamos, todas las razones trigonométricas son positivas en el primer cuadrante.
Entonces, usando las fórmulas,
bronceado x =
Por lo tanto, los valores de las otras cinco funciones trigonométricas son: cos x = 4/5, tan x = 3/4, cosec x = 5/3, sec x = 5/4, cot x = 4/3
Pregunta 2. Si sen x = 12/13 y está en el segundo cuadrante, encuentra el valor de sec x + tan x.
Solución:
Dado:
Sin x =
y x está en el segundo cuadrante.
Sabemos que, en el segundo cuadrante, sen x y cosec x son positivos y todas las demás razones son negativas.
Entonces, usando las fórmulas, obtenemos
porque x =
tan x = sen x/cos x
seg x = 1/cos x
sec x + tan x = ((-13/5) +(-12/5))
= (-13 – 12)/5 = -25/5 = -5
Por lo tanto, el valor de Sec x + tan x = -5
Pregunta 3. Si sen x = 3/5, tan y = 1/2 y π /2 < x < π < y < 3 π /2 encuentra el valor de 8 tan x -√5 seg y.
Solución:
Dado, sen x = 3/5, tan y = 1/2, y π /2 < x< π< y< 3 π /2
Aquí, x está en el segundo cuadrante y y está en el tercer cuadrante. Entonces, cos x y
tan x son negativos en el segundo cuadrante y sec y es negativo en el tercer cuadrante.
Entonces, usando la fórmula, obtenemos
porque x =
tan x = sen x/ cos x
porque x =
Sabemos que seg y =
8tan x – √5 seg y = 8 × (-3)/(4) – √5 × (-√5/2) = -6 + (5/2) = (-12 + 5)/2 = -7 /2
8tan x – √5 seg y = -7/2
Por lo tanto, el valor de 8 tan x – √5 seg y = -7/2
Pregunta 4. Si sen x + cos x = 0 y x está en el cuarto cuadrante, encuentra sen x y cos x.
Solución:
Dado, sen x + cos x = 0 y x se encuentra en el cuarto cuadrante.
sen x = -cos x
sen x/cos x = -1
Entonces, tan x = -1 (ya que, tan x = sen x/cos x)
cos x y sec x son positivos en el cuarto cuadrante y
todas las demás proporciones son negativas.
Entonces, usando las fórmulas,
segundo x =
cos x = 1/seg x
sen x =
segundo x =
Por lo tanto, el valor de sen x = -1/√2 y cos x = 1/√2
Pregunta 5. Si cos x = -3/5 y π < x < 3π/2, encuentre los valores de otras cinco funciones trigonométricas y, por lo tanto, evalúe 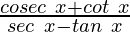
Solución:
Dado, cos x = -3/5 y π <x < 3π/2
tan x y cot x son positivas en el tercer cuadrante y todas las demás proporciones son negativas.
Ahora, usando las fórmulas, obtenemos
sen x = –
tan x = sen x/cos x
cuna x = 1/bronceado x
seg x = 1/cos x
cosec x = 1/sen x
sen x =
bronceado x =
cuna x =
segundo x =
cosec x =
Ahora evaluamos:
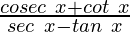
Publicación traducida automáticamente
Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
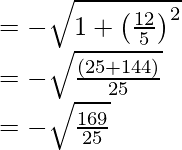
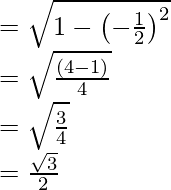
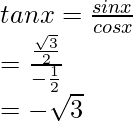
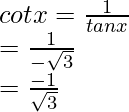
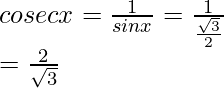
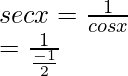
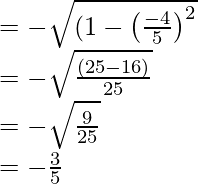
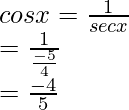
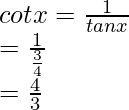
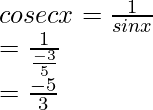
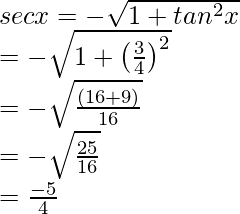
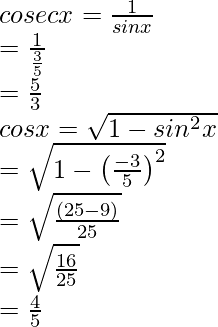
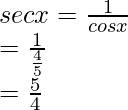
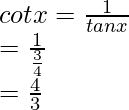
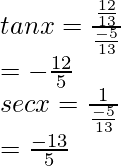
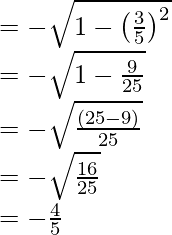
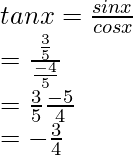
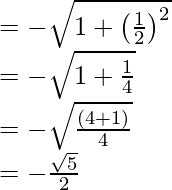
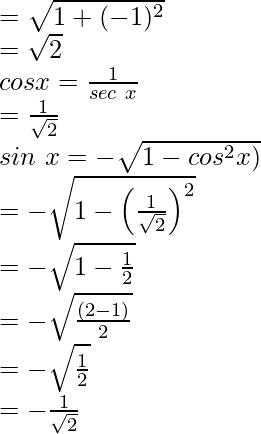
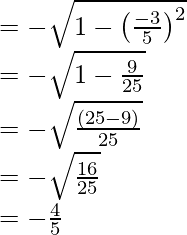
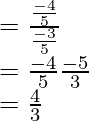
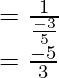
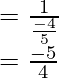
![Rendered by QuickLaTeX.com = \frac{\left[\frac{-5}{4} + \frac{3}{4}\right] }{ \left[\frac{-5}{3} - \frac{4}{3}\right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9dcb5dd7992b7f381d91e7a4338cecc7_l3.png)
![Rendered by QuickLaTeX.com \\ = \frac{\left[\frac{(-5+3)}{4}\right] }{ \left[\frac{(-5-4)}{3}\right]}\\ = \frac{\frac{-2}{4} }{ \frac{-9}{3}}\\ = \frac{-1}{\frac{2} {-3}}\\ = \frac{1}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e13dd7cc33bb3b8e810dc546f8bf392d_l3.png)