Clase 11 Soluciones RD Sharma – Capítulo 5 Funciones trigonométricas – Ejercicio 5.3

Pregunta 1. Encuentra los valores de las siguientes razones trigonométricas:

(i) sen 5π/3

Solución:

Tenemos, sen 5π/3

=sen (2π-π/3) [∵sen(2π-θ)=-senθ]

=-sin(π/3)

= – √3/2

(ii) sen 17π

Solución:

Tenemos, pecado 17π

⇒sen 17π=sen (34×π/2)

Dado que 17π se encuentra en el eje x negativo, es decir, entre el segundo y el tercer cuadrante 

=sen 17π [∵ sin nπ=0] 

= 0

(iii) tan11π/6

Solución:

Claramente, tan(11π/6) = tan ((12π-π)/6)

= bronceado (4π/2-π/6)

claramente, el ángulo se encuentra en el IV cuadrante en el que la función tangente es negativa y el múltiplo de π/2 es par.

= bronceado (4π/2-π/6)= -cot (π/6)

=-1/√3

(iv) coseno (-25π/4)

Solución:

La función coseno es una función par, por lo tanto, 

coseno (-25π/4)=coseno (25π/4)

Ahora, 25π/4=(12×π/2+π/4)  

25π/4 se encuentra en el cuadrante I e incluso múltiplo de π/2 

coseno (25π/4)=coseno (12×π/2+π/4)=coseno π/4=1/√2  

(v) bronceado (7π/4)

Solución:

Tenemos, 7π/4=(8π-π)/4 = 2π-π/4

=tan (2π-π/4) [∵ tan(2π-θ)=-tanθ]    

=-tan π/4

=-1

(vi) sen 17π/6

Solución:

sen 17π/6= sen (3π-π/6)

=sen (2π+(π-π/6))

=sen (π-π/6) [∵ sin(2π+θ)=senθ]    

=sen π/6 [∵ sin(π-θ)=senθ]    

=1/2

(vii) cos 19π/6 

Solución:

cos 19π/6 = cos (3π+(π+π/6))

= coseno (2π+(π+π/6))

=cos (π+π/6) [∵ cos(2π+θ)= cosθ)]

=-cos π/6 [∵ cos(π+θ)=-cosθ]

=-√3/2

(viii) pecado (-11π/6)

Solución:

pecado (-11π/6) = pecado (-(2π-π/6))

=sin (2π-π/6) [∵ sin(-θ)= -sinθ] 

=-(-sin π/6) [∵ sin(2π-θ)= -sinθ] 

= sen π/6

=1/2

(ix) cosec (-20π/3)

Solución:

cosec (-20π/3)= cosec (-(7π-π/3))

= cosec (7π-π/3) [∵ cosec(-θ) = -cosecθ]

= – cosec (2×3π+ (π-π/3))

= – cosec (π-π/3)           

= – cosec π/3 [∵ cosec(π-θ)= cosecθ] 

= – 2/√3

(x) bronceado (-13π/4)

Solución:

tan (-13π/4) = -tan (13π/4) [∵ tan(-θ)=-tanθ]    

=-bronceado (3π+π/4)

=- tan (2π+(π+π/4) [∵ tan(2π+θ)=tanθ]

=-tan π/4 [∵ tan(π+θ)=tanθ]          

= -1

(xi) cos 19π/4  

Solución:

cos 19π/4 = cos (5π-π/4))

= cos (2×2π+(π-π/4)) [∵ cos(2nπ+θ)= cosθ , n ∈ N]  

=cos (π-π/4) [∵ cos(π-θ)= -cosθ]

=-cos π/4

=-1/√2

(xii) pecado (41π/4)

Solución:

pecado (41π/4) = pecado (10π+π/4)

=sin (2×5π+π/4) [∵ sin(-θ)= -sinθ]  

=sen π/4 [∵ sin(2π-θ)= -senθ]  

=1/√2

(xiii) cos 39π/4  

Solución:

cos 39π/4 = cos (10π-π/4))

= coseno (2×5π-π/4)

=cos π/4 [∵ cos(2nπ-θ)= cosθ , n ∈ N]

=1/√2

(xiv) pecado (151π/6)

Solución:

pecado (151π/6) = pecado (25π+π/6)

=sin (2×12π+ (π +π/6)) [∵ sin(2nπ+θ)= sinθ , n ∈ N]  

=sin (π +π/6) [∵ sin(π+θ)= -sinθ]  

=-sen π/6

=-1/2

Pregunta 2. Demuestra que:

(i) bronceado 225° cuna 405°+tan 765° cuna 675°=0

Solución:

Tomando LHS

bronceado 225° cuna 405°+bronceado 765° cuna 675°

= bronceado (π+π/4) cuna (2π+π/4)+tan (4π+π/4) cuna (4π-π/4)

=tan(π/4)×cot(π/4)+tan(π/4)×{-cot(π/4)} [∵ cot(4π-π/4)=-cot(π/4)]  

=1×1+1×(-1)

=0 = RHS (por lo tanto probado)

(ii) sen (8π/3) cos (23π/6)+cos (13π/3) sen (35π/6)=1/2

Solución:

Tomando LHS

sen (8π/3) cos (23π/6)+cos (13π/3) sen (35π/6)

=sen (3π-π/3) cos (4π-π/6)+cos (4π+π/3) sen (6π-π/6)

=sin (π/3) cos (π/6)+cos (π/3) {-sin (π/6)} [∵ sin(6π-θ)= -sinθ]

=√3/2×√3/2+1/2×(-1/2)

=3/4-1/4

=2/4

=1/2= RHS (por lo tanto probado)

(iii) cos 24° + cos55° + cos125° + cos204° + cos300°=1/2

Solución:

Tomando LHS

cos 24° + cos 55° + cos 125° + cos 204° + cos 300°

= cos 24° – cos ( π+24°) + cos 55° + cos (π-55°) + cos ( 2π-π/3)

= cos 24° – cos 24° + cos 55° – cos 55° + cos π/3

= cos π/3

= 1/2 = RHS (por lo tanto probado)

(iv) tan (-225°) cot (-405°)-tan (-765°) cot (675°) = 0

Solución:

Tomando LHS

bronceado (-225°) cuna (-405°)-tan (-765°) cuna (675°)

=-tan 225° {-cot 405°}+tan 765° cuna 675°

= bronceado (π+π/4) cuna (2π+π/4)+tan (4π+π/4) cuna (4π-π/4)

=tan(π/4) cot(π/4)+tan(π/4)×{-cot(π/4)} [∵ cot(4π-π/4)=-cot(π/4)]

=1×1+1×(-1)

=1-1

=0 = RHS (por lo tanto probado)

(v) cos 570° sen 510° + sen (-330°) cos (-390°)=0

Solución:

Tomando LHS

cos 570° sen 510° + sen (-330°) cos (-390°)

=cos (3π+π/6) sin (3π-π/6) – sin 330° cos 390° [∵ sin(-θ)= -sinθ y cos(-θ)= cosθ]

=-cos π/6 sen π/6 + sen π/6 cos π/6 [∵ sen(2π-θ)= -sinθ]

=0=RHS (por lo tanto probado)

(vi) tan (11π/3)- 2sin (4π/6)-3/4cosec ² (π/4)+4cos ² (17π/6)=(3-4√3)/2

Solución:

Tomando LHS

tan (4π-π/3)- 2sen (2π/3)-3/4×(√2) ² +4cos ² (3π-π/6)

=-tan π/3- 2sin (π-π/3)-3/4×2+4cos ² π/6 [∵ tan(nπ-θ)=-tanθ ∵cos(2nπ-θ)= -cosθ , n ∈ N]   

=-√3 – 2sen π/3 -3/2+4×(√3/2) ²

=-√3 – 2×(√3/2) -3/2+4×(3/4)

=-√3 – √3 -3/2+3

=-2√3+(-3+6)/2

=-2√3+3/2

=(3-4√3)/2=RHS (Por lo tanto probado)

(vii) 3sen (π/6) seg (π/3)- 4sen (5π/6) cot (π/4)=1

Solución:

Tomando LHS

3sin (π/6) seg (π/3)- 4sin (5π/6) cot (π/4)

=3×(1/2)×2- 4sen (π-π/6)×1

=3 – 4sen π/6

=3-4×1/2

=3-2=1=RHS (por lo tanto probado)

Pregunta 3. Demuestra que:

(i) 

Solución:

                                        [∵tan(π/2+θ)= -cotθ]

=                                                    [∵seg(π/2+θ)= -cosecθ]

=1

=RHS (por lo tanto probado)

(ii) =2

Solución: 

Tomando LHS

=                                [∵cot(π/2+θ)= -tanθ ∵cot(2π+θ)= cotθ]]

=(sec x+cot(π/2+x))/(secx-tanx)+1

=(seg x-tanx)/(segx-tanx)+1

=1+1

=2=RHS (por lo tanto probado)

{iii}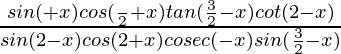 =1

Solución:

Tomando LHS

           [∵ tan(π/2-θ)= cotθ ∵sin(π/2+θ)= -cosθ]

=                                 [∵ cotθ= cosθ/sinθ ∵ cosecθ= 1/sinθ]

=

= 1 = RHS (por lo tanto probado)

(iv) {1+cot x -seg(π/2+x)}{1+cot x + sec(π/2+x)}=2cot x 

Solución:

Tomando LHS

{1+cot x -sec(π/2+x)}{1+cot x + sec(π/2+x)} [∵ sec(π/2+θ)= -cosecθ]

={1+cot x -(-cosec x)}{1+cot x – cosec x}

={(1+cot x) +cosec x}{(1+cot x) – cosec x}

=(1+cuna x) ² -coseg ² x

=1+cot ² x+2cot x -cosec ² x [∵ 1+cot ² θ=cosec ² θ]

=coseg ² x+2cot x -coseg ² x

=2cot x=RHS (por lo tanto probado)

(v)  =1

Solución:

Tomando LHS

=

=1=RHS (por lo tanto probado)

Pregunta 4. Prueba que: sin ² π/18+sin ² π/9+sin ² 7π/18+sin ² 4π/9=2

Solución:

Tomando LHS

sen ² π/18+sen ² π/9+sen ² 7π/18+sen ² 4π/9

=sen ² (π/2-4π/9)+sen ² 4π/9+sen ² π/9+sen ² (π/2-π/9)

=cos ² 4π/9+sen ² 4π/9+sen ² π/9+cos ² π/9

=1+1=2=RHS (por lo tanto probado)

Pregunta 5. Demuestra que: sec(3π/2-x)sec(x-5π/2)+tan(5π/2+x)tan(x-3π/2)=-1

Solución:

Tomando LHS:

segundo(3π/2-x)segundo(x-5π/2)+bronceado(5π/2+x)bronceado(x-3π/2)

=sec(3π/2-x)sec(-(5π/2-x))+tan(5π/2+x)tan(-(3π/2-x)) [∵sec(-θ)=secθ]

=-cosec x seg(5π/2-x)-cot x (-tan(3π/2-x))

=-cosec x cosec x-cot x (-cot x)

=-cosec ² x + cot ² x

=-cosec ² x + cosec ² x – 1 [∵1+cot ² θ=cosec ² θ]

=-1=RHS (por lo tanto probado)

Pregunta 6. En un △ABC, prueba que:

(i) coseno (A+B) + coseno C = 0

Solución:

A+B+C=π

A+B=π-C ———-(1)

Tomando LHS

porque (A+B) + porque C

Poniendo el valor de A+B 

cos (π-C) + cos C [∵ cos(π-θ)= -cosθ]  

=-cos C+ cos C

=0 = RHS (por lo tanto probado)

(ii) cos (A+B)/2=sen C/2

Solución:

Tomando LHS

porque (A+B)/2

Poniendo el valor de A+B de (1)

=cos (π-C)/2

=cos(π/2-C/2) [∵ cos(π/2+θ)= senθ]

=sen C/2 = RHS (por lo tanto probado) 

(iii) bronceado (A+B)/2=cot C/2

Solución:

Tomando LHS

bronceado (A+B)/2

Poniendo el valor de A+B de (1)

= bronceado (π-C)/2

=tan (π/2-C/2) [∵ tan(π/2-θ)= cotθ]

=cot C/2 = RHS (Por lo tanto Probado) 

Pregunta 7. Si A,B,C,D son los ángulos de un cuadrilátero cíclico, tomados en orden, demuestre que

cos(180°-A)+cos(180°+B)+cos(180°+C)-sen(90°+D)=0

Solución:

Como A, B, C, D son los ángulos de un cuadrilátero cíclico

Por lo tanto, A+B+C+D=2π

o A+B=π o C+D=π

A=π-B también C=π-D

Tomando LHS

cos(180°-A)+cos(180°+B)+cos(180°+C)-sen(90°+D)

=cos(π-(π-B))+cos(π+B)+cos(π+(π-D))-sin(π/2+D) [∵ cos(π+θ)= -cosθ]

=cos B +(-cos B) +cos D -cos D

=cos B – cos B +0

=0 =RHS (por lo tanto probado)    

Pregunta 8. Halla x a partir de las siguientes ecuaciones

(i) cosec (π/2+θ) + x cos θ cot(π/2+θ)=sin(π/2+θ)

Solución:

Tenemos,

cosec (π/2+θ) + x cos θ cot(π/2+θ)=sin(π/2+θ)

⇒ sec θ + x cos θ (-tanθ)=cos θ

⇒1/cosθ – x cos θ (senθ/cosθ)=cos θ

⇒1/cosθ – x senθ=cos θ

⇒1-x senθcosθ/cosθ =cos θ

⇒1-x senθcosθ =cos ² θ

⇒1-cos ² θ =x senθcosθ

⇒sen ² θ =x senθcosθ

⇒x=senθ/cosθ

⇒x=tanθ

(ii) x cot (π/2+θ) + tan (π/2+θ)sen θ+ cosec(π/2+θ)=0

Solución:

Tenemos,

x cot (π/2+θ) + tan (π/2+θ)sen θ+ cosec(π/2+θ)=0

⇒-x tan θ – cot θ sen θ+ sec θ=0

⇒-x sen θ/cos θ – (cos θ/sen θ) sen θ+ 1/cos θ=0

⇒-x sen θ/cos θ – cos θ + 1/cos θ=0

⇒(-x sen θ – cos ² θ + 1)/cos θ=0

⇒-x sen θ +1- cos ² θ =0

⇒-x sen θ + sen ² θ =0

⇒x sen θ = sen ² θ =0

⇒x = sen θ 

Pregunta 9. Demostrar que:

(i) tan 4π – cos (3π/2)-sen (5π/6)cos (2π/3)=1/4

Solución:

Tomando LHS

tan 4π – cos (3π/2)-sen (5π/6)cos (2π/3) [∵ tan nπ= 0, ∀ n∈ Z ]

=0- coseno (π+π/2)-sen (π-π/6)coseno(π/2-π/6)          

=0- (cos π/2)- (sen π/6)(-sen π/6)

=0-0+sen ² π/6

=(1/2) ²

=1/4=RHS (por lo tanto probado)

(ii) sen (13π/3) sen (8π/3) + cos (2π/3) sen (5π/6)=1/2

Solución:

Tomando LHS

sen (13π/3) sen (8π/3) + coseno (2π/3) sen (5π/6)

=sin (4π+π/3) sin (3π-π/3) + coseno (π/2+π/6)sin (π-π/6) [∵ sin (4π+θ)= sinθ & sin (3π -θ)= senθ]

=sen π/3 sen π/3 + (-sen π/6) sen π/6

=(√3/2)×(√3/2)-(1/2)×(1/2)

=3/4-1/4

=2/4=1/2=RHS (por lo tanto probado)

(iii) sen (13π/3) sen (2π/3) + cos (4π/3) sen (13π/6)=1/2

Solución:

Tomando LHS

sen (13π/3) sen (2π/3) + coseno (4π/3) sen (13π/6)

=sen (4π+π/3) sen (π/2-π/6) + coseno (π+π/6)sen (2π+π/6)

= sen π/3 cos π/6 – cos π/3 sen π/6

=(√3/2)×(√3/2)-(1/2)×(1/2)

=3/4-1/4

=2/4=1/2=RHS (por lo tanto probado)

(iv) sen (10π/3) cos (13π/6) + cos (8π/3) sen (5π/6)=-1

Solución:

Tomando LHS

sen (10π/3) cos (13π/6) + cos (8π/3) sen (5π/6)

=sen (3π+π/3) coseno (2π+π/6) + coseno (3π-π/3)sen (π-π/6)

=-sin (π/3) cos (π/6) + cos π/3 (- sin π/6) [∵ sin (3π+θ)= -sinθ & cos (3π-θ)= -cosθ]

=(-√3/2)×(-√3/2)-(1/2)×(1/2)

=-3/4-1/4

=-4/4=-1=RHS (por lo tanto probado)

(V) bronceado (5π/4) cuna (9π/4) + bronceado (17π/4) cuna (15π/4)=0

Solución:

Tomando LHS

bronceado (5π/4) cuna (9π/4) + bronceado (17π/4) cuna (15π/4)

= bronceado (π+π/4) cuna (2π+π/4) + bronceado (4π+π/4) cuna (4π-π/4)

=(tan π/4) (cot π/4) + (tan π/4) (-cot π/4)

=1.1+1.(-1)

=1-1=0 RHS (por lo tanto probado)