Dibujar las gráficas de las siguientes funciones:
Pregunta 1: y = sen 2 x
Solución:
Como sabemos que,
y = sen 2 x =
Al desplazar el origen en (0, 1/2), obtenemos
X = x e Y =
Al sustituir estos valores, obtenemos
Los valores máximo y mínimo de Y son
y
respectivamente y lo desplazan 1/2 hacia arriba.
Como la ecuación en forma de y = – f(x), la gráfica se invierte de y = f(x)
Pregunta 2: y = cos 2 x
Solución:
Como sabemos que,
y = cos 2 x =
Al desplazar el origen en
, obtenemos
X = x e Y =
Al sustituir estos valores, obtenemos
Los valores máximo y mínimo de Y son
Pregunta 3: y = sen 2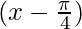 
Solución:
Para obtener esta gráfica y-0 = sen 2
Al desplazar el origen en (
,0), obtenemos
X =
y Y = y – 0
Al sustituir estos valores, obtenemos
Y = sen 2 X
Primero dibujamos la gráfica de Y = sen 2 X y la desplazamos π/4 hacia la derecha.
Pregunta 4: y = tan 2x
Solución:
Para obtener este gráfico y = tan 2x,
Primero dibujamos la gráfica de y = tan x y luego dividimos las coordenadas x de los puntos donde cruza el eje x por 2.
Pregunta 5: y = 2 tan 3x
Solución:
Para obtener este gráfico y = 2 tan 3x,
Primero dibujamos la gráfica de y = tan x y luego dividimos las coordenadas x de los puntos donde cruza el eje x por 3.
Estira el gráfico verticalmente por el factor de 2.
Pregunta 6: y = 2 cuna 2x
Solución:
Para obtener este gráfico y = 2 cot 2x,
Primero dibujamos la gráfica de y = cot x y luego dividimos las coordenadas x de los puntos donde cruza el eje x por 2.
Estira el gráfico verticalmente por el factor de 2.
Dibujar las gráficas de las siguientes funciones en la misma escala:
Pregunta 7: y = cos 2 x, y = cos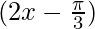 
Solución:
Gráfico 1:
y = cos 2 x
Como sabemos que,
y = cos 2 x =
Al desplazar el origen en (0, 1/2), obtenemos
X = x e Y =
Al sustituir estos valores, obtenemos
Los valores máximo y mínimo de Y son
Gráfico 2:
Para obtener este gráfico y-0 = cos (2x-
) = cos 2(x-
)
Al desplazar el origen en (π/6, 0), obtenemos
X =
y Y = y – 0
Al sustituir estos valores, obtenemos
Y = cos 2X
Primero dibujamos la gráfica de Y = cos 2X y la desplazamos π/6 hacia la derecha.
La gráfica y = cos 2 x y y = cos
están en los mismos ejes es la siguiente:
Pregunta 8: y = sen 2 x, y = sen x
Solución:
Gráfico 1:
y = sen 2 x
Como sabemos que,
y = sen 2 x =
Al desplazar el origen en (0,
X = x e Y =
Al sustituir estos valores, obtenemos
Los valores máximo y mínimo de Y son
Como la ecuación en forma de y = – f(x), la gráfica se invierte de y = f(x)
Gráfico 2:
y = sen x
La gráfica y = sen 2 x y y = sen x están en los mismos ejes son las siguientes:
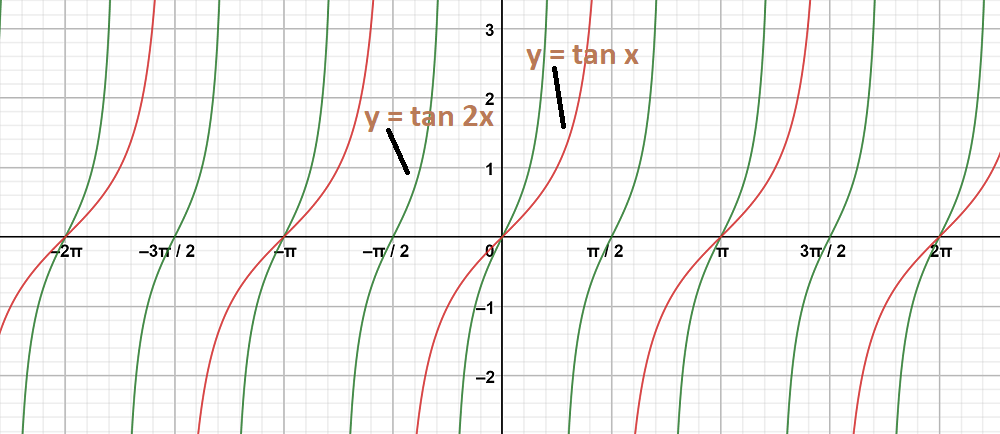
Pregunta 9: y = tan x, y = tan 2 x
Solución:
Gráfico 1:
y = bronceado x
Gráfico 2:
y = bronceado 2 x
El gráfico y = tan x y y = tan 2 x están en los mismos ejes son los siguientes:
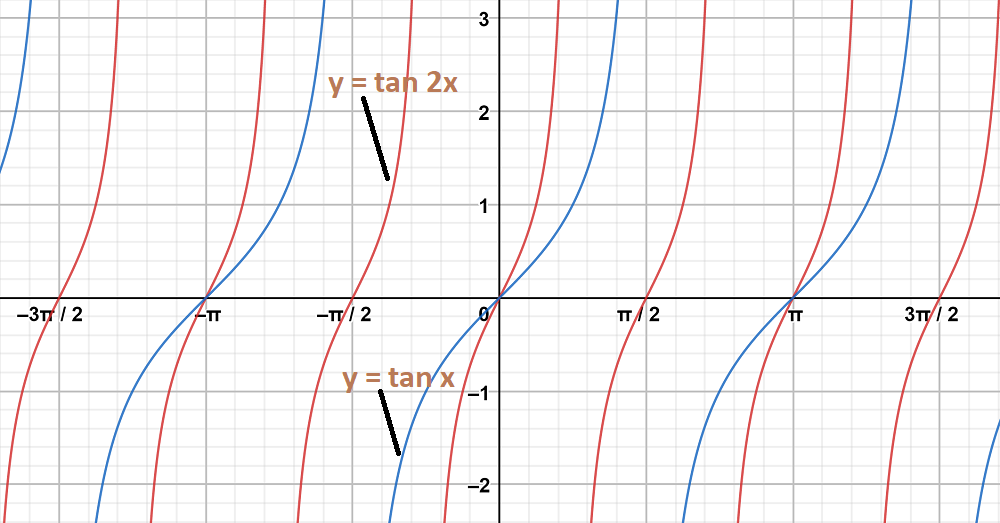
Pregunta 10: y = tan 2x, y = tan x
Solución:
Gráfico 1:
Para obtener este gráfico y = tan 2x,
Primero dibujamos la gráfica de y = tan x y luego dividimos las coordenadas x de los puntos donde cruza el eje x por 2.
Gráfico 2:
y = bronceado x
El gráfico y = tan 2x y y = tan x están en los mismos ejes son los siguientes:
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA