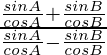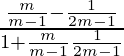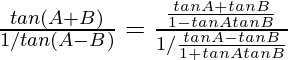Clase 11 Soluciones RD Sharma – Capítulo 7 Razones trigonométricas de ángulos compuestos – Ejercicio 7.1 | Serie 1

Pregunta 1. Si sen A = 4/5 y cos B = 5/13, donde 0 < A, B < π/2, encuentre los valores de lo siguiente:

(i) pecado (A + B)

(ii) porque (A + B)

(iii) pecado (A – B)

(iv) porque (A – B)

Solución:

Dado que

sen A = 4/5 y cos B = 5/13

Como sabemos, cos A = (1 – sen ² A) y sen B = (1 – cos ² B), donde 0 <A, B < π/2

Ahora encontramos el valor de cosA y senB

cos A = √(1 – sen ² A)

= √(1 – (4/5) ² ) 

= √(1 – (16/25))

= √((25 – 16)/25)

= √(9/25)

= 3/5

sen B = √(1 – cos ² B)

= √(1 – (5/13) ² )

= √(1 – (25/169))

= √(169 – 25)/169)

= √(144/169)

= 12/13

(i) pecado (A + B)

sen (A + B) = senA cosB + cosA senB

= 4/5 × 5/13 + 3/5 × 12/13

= 20/65 + 36/65 

= (20 + 36)/65

= 56/65

(ii) porque (A + B)

cos (A + B) = cosA cosB – senA senB

= 3/5 × 5/13 – 4/5 × 12/13

= 15/65 – 48/65

= -33/65

(iii) pecado (A – B)

sen (A – B) = senA cosB – cosA senB

= 4/5 × 5/13 – 3/5 × 12/13

= 20/65 – 36/65

= – 16/65

(iv) porque (A – B)

cos (A – B) = cos A cos B + sen A sen B

= 3/5 x 5/13 + 4/5 x 12/13

= 15/65 + 48/65

= 63/65

Pregunta 2. (a) Si senA = 12/13 y sen B = 4/5, donde π/2 < A <π y 0 < B π/2, encuentre lo siguiente:

(i) pecado (A + B) 

(ii) porque (A + B)

Solución:

Tenemos,

sinA = 12/13 y sinB = 4/5, donde π/2 < A < y 0 < B < π/2

Como sabemos, cosA = – √(1 – sen ² A) y cosB = √(1 – sen ² B)

Ahora encontramos el valor de cosA y cosB

cosA = – √(1 – sen ² A)

= – √(1 – (12/13) ² )

= – √(1 – 144/169)

= – √((169 – 144)/169)

= – √(25/169)

= – 5/13

cosB = √(1 – sen ² B)

= √(1 – (4/5) ² )

= √(1 – 16/25)

= √((25 – 16)/25)

= √(9/25)

= 3/5

(i) pecado (A + B)

Ya que, sen (A + B) = senA cosB + cosA senB

= 12/13 x 3/5 + (-5/13) x 4/5

= 36/65 – 20/65

= 16/65

(ii) porque (A + B)

Ya que, cos (A + B) = cos A cos B – sen A sen B

= – 5/13 x 3/5 – 12/13 x 4/5

= – 15/65 – 48/65

= – 63/65

(b) Si senA = 3/5, cosB = 12/13, donde A y B, ambos se encuentran en el segundo cuadrante, encuentre el valor de sen (A + B).

Solución:

Tenemos,

sinA = 3/5, cosB = -12/13, donde A y B, ambos se encuentran en el segundo cuadrante.

Como sabemos cosA = – √(1- sen ² A) y senB = √(1 – cos ² B)

Ahora encontramos el valor de cosA y senB

cos A = – √(1 – sen ² A)

= -√(1 – (3/5) ² )

= -√(1 – 9/25)

= – √((25 – 9)/25)

= – √(16/25)

= – 4/5

senB = √(1 – cos ² B)

= √(1 – (-12/13)2)

= √(1 – 144/169)

= √((169 – 144)/169)

= √(25/169)

= 5/13

Necesitamos encontrar el valor del pecado (A + B)

Ya que, sen (A + B) = senA cosB + cosA senB

= 3/5 × (-12/13) + (-4/5) × 5/13

= -36/65 – 20/65

= -56/65

Pregunta 3. Si cosA = -24/25 y cosB = 3/5, donde π < A < 3π/2 y 3π/2 < B < 2π, encuentre lo siguiente:

(i) sen(A + B) 

(ii) cos(A + B)

Solución:

Tenemos,

cosA = -24/25 y cosB = 3/5, donde π < A < 3π/2 y 3π/2 < B < 2π

Como sabemos que A está presente en el tercer cuadrante, B está 

presente en el cuarto cuadrante, por lo que la función seno es Negativa.

Usando las fórmulas, sinA = √(1 – cos ² A) y sinB = -√(1 – cos ² B)

Encontramos el valor de sinA y sinB

senA = – √(1 – cos ² A)

= – √(1 – (-24/25) ² )

= – √(1 – 576/625)

= – √((625 – 576)/625)

= – √(49/625)

= – 7/25

senB = – √(1 – cos ² B)

= – √(1 – (3/5)²)

= – √(1 – 9/25) 

= – √((25 – 9)/25)

= – √(16/25)

= – 4/5

(i) pecado (A + B)

Ya que, sen (A + B) = senA cosB + cosA senB

= -7/25 x 3/5 + (-24/25) x (-4/5)

= -21/125 + 96/125

= 75/125

= 3/5

(ii) porque (A + B)

Ya que, cos (A + B) = cosA cosB – sinA sinB

= (-24/25) x 3/5 – (-7/25) × (-4/5)

= – 72/125 – 28/125

=- 100/125

= – 4/5

Pregunta 4. Si tanA = 3/4, cosB = 9/41, donde π < A < 3π/2 y 0 < B < π/2, encuentre tan(A + B).

Solución:

Tenemos,

tanA = 3/4 y cosB = 9/41, donde π < A < 3π/2 y 0 < B < π/2

Como sabemos que, A está presente en el tercer cuadrante, B está presente en el primer cuadrante

Entonces, las funciones tan y sin son positivas.

Ahora usando la fórmula,

senB = √(1 – cos ² B)

Hallamos el valor de sen B.

senB = √(1 – cos ² B)

= √(1 – (9/41) ² )

= √(1 – 81/1681)

= √((1681 – 81)/1681)

= √(1600/1681)

= 40/41

Como sabemos que, tanB = senB/cosB, entonces

= (40/41)/(9/41)

= 40/9

Dado que, tan(A + B) = (tanA + tanB)/(1 – tanA tanB), entonces

= (3/4 + 40/9)/(1 – 3/4 x 40/9)

= (187/36)/(1 – 120/36)

= (187/36)/((36 – 120)/36)

= (187/36)/(- 84/36)

= -187/84

Por lo tanto, tan(A + B) = -187/84

Pregunta 5. Si sinA = 1/2, cosB = 12/13, donde π/2 < A < π y 3π/2 < B < 2π, encuentre tan(A – B).

Solución:

Tenemos,

sinA = 1/2, cosB = 12/13, donde π/2 < A < π y 3π/2 < B < 2π

Como sabemos, A está presente en el segundo cuadrante y B está presente en el cuarto cuadrante.

Entonces, la función seno es positiva, las funciones coseno y tan son negativas en el segundo cuadrante

y las funciones seno y tan son negativas, la función coseno es positiva en el cuarto cuadrante

Ahora usando las siguientes fórmulas,

cosA = -√(1 – sen ² A) y senB = -√(1 – cos ² B)

Encontramos el valor de cosA y senB

cosA = – √(1 – sen ² A)

= – √(1 – (1/2) ² )

= – √(1 – 1/4)

= – √((4 – 1)/4)

= – √(3/4)

= – √3/2

senB = – √(1 – cos ² B)

= – √(1 – (12/13) ² )

= – √(1 – 144/169)

= – √((169 – 144)/169)

= – √(25/169)

= – 5/13

Como sabemos, tanA = sinA/cosA y tanB = sinB / cosB

tanA = (1/2)/(-√3/2) = -1/√3 y

tanB = (-5/13)/(12/13) = -5/12

Dado que, tan (A – B) = (tanA – tanB) / (1 + tanA tanB), entonces

= ((-1/√3) – (-5/12)) / (1 + (-1/√3) x (-5/12))

= ((-12 + 5√3)/12√3) / (1 + 5/12√3)

= ((-12 + 5√3)/12√3) / ((12√3 + 5)/12√3)

= (5√3 – 12)/(5 + 12√3)

Por lo tanto, tan (A – B) = (5√3 – 12)/(5 + 12√3)

Pregunta 6. Si sinA = 1/2, cosB = √3/2, donde π/2 < A < π y 0 < B < π/2, encuentre lo siguiente:

(i) bronceado (A + B) 

(ii) bronceado (A – B) 

Solución:

Tenemos,

SinA = 1/2 y cosB = √3/2, donde π/2 < A < π y 0 < B < π/2

Como sabemos que A está en el segundo cuadrante, B está en el primer cuadrante.

Entonces, todas las funciones son positivas en el primer cuadrante y la función seno es positiva, 

Las funciones coseno y tan son negativas en el segundo cuadrante. 

Entonces, usando las siguientes fórmulas,

cosA = – √(1 – sen ² A) y senB = √(1 – cos ² B)

Encontramos el valor de cosA y senB

cosA = – √(1 – sen ² A)

= – √(1 – (1/2) ² )

= – √(1 – 1/4)

= – √((4 – 1)/4)

= – √(3/4)

= – √3/2

senB = √(1 – cos ² B)

= √(1 – (√3/2) ² )

= √(1 – 3/4)

= √((4 – 3)/4)

= √(1/4)

= 1/2

Como sabemos que, tanA = sinA / cosA y tanB = sinB / cosB

Entonces, tanA = (1/2)/(-√3/2) = -1/√3 y

tanB = (1/2)/(√3/2) = 1/√3

(i) Dado que, tan(A + B) = (tanA + tanB)/(1 – tanA tanB), entonces

= (-1/√3 + 1/√3)/(1 – (-1/√3) × 1/√3)

= 0/(1 + 1/3)

= 0

Por lo tanto, tan(A + B) = 0

(ii) Dado que, tan(A – B) = (tanA – tanB)/(1 + tanA tanB), entonces

= ((-1/√3) – (1/√3))/(1 + (-1/√3) x (1/√3))

= ((-2/√3)/(1 – 1/3)

= ((-2/√3)/(3 – 1)/3)

= ((-2/√3)/2/3)

= -√3

Por lo tanto, tan(A – B) = -√3

Pregunta 7. Evalúa lo siguiente:

(i) sen 78° cos 18⁰- cos 78° sen 18⁰ 

(ii) cos 47° cos 13⁰ – sen 47⁰ sen 13⁰ 

(iii) sen 36° cos 9⁰+ cos 36° sen 9⁰ 

(iv) cos 80° cos 20⁰+ sen 80° sen 20⁰ 

Solución:

(i) sen 78° cos 18° – cos 78° sen 18°

Ya que, sinAcosB – cosAsinB = sin(A – B)

Asi que

sen 78° cos 18° – cos 78° sen 18° = sen(78 – 18)°

= sen 60°

= √3/2

(ii) cos 47° cos 13° – sen 47° sen 13°

Ya que, cosA cosB – senA senB = cos(A + B)

Entonces, cos 47° cos 13° – sen 47° sen 13° = cos (47 + 13)°

= cos 60°

= 1/2

(iii) sen 36° cos 9° + cos 36° sen 9°

Ya que, sen A cos B + cos A sen B = sen (A + B) 

Entonces, sen 36° cos 9° + cos 36° sen 9° = sen (36 + 9)°

= sen 45°

= 1/√2

(iv) cos 80° cos 20° + sen 80° sen 20⁰

Ya que, cos A cos B + sen A sen B = cos (A – B)

Entonces, cos 80° cos 20° + sen 80° sen 20° = cos (80 – 20)°

= cos 60°

= 1/2

Pregunta 8. Si cosA = -12/13 y cotB = 24/7, donde A se encuentra en el segundo cuadrante y B en el tercero, encuentre los valores de lo siguiente:

(i) sen(A + B) 

(ii) cos(A + B) 

(iii) bronceado (A + B)

Solución:

Tenemos,

cosA = -12/13 y cotB= 24/7

Se da que, A se encuentra en el segundo cuadrante, B en el tercer cuadrante.

Entonces, la función seno es positiva en el segundo cuadrante y tanto el seno como el coseno 

Las funciones son negativas en el tercer cuadrante.

Entonces, usando las siguientes fórmulas,

senA = √(1 – cos ² A), senB = 1/√(1 + cot ² B) y cosB = -√(1 – sen ² B),

Encontramos el valor de sinA y sinB

senA = √(1 – cos ² A)

= √(1 -(-12/13) ² )

= √(1 – 144/169) 

= √((169 – 144)/169)

= √(25/169)

= 5/13

senB = -1/√(1 + cuna ² B)

= -1/√(1 + (24/7) ² )

= -1/√(1 + 576/49)

= -1/√((49 + 576)/49)

= -1/√(625/49)

= -1/(25/7)

= -7/25

cosB = -√(1 – sen ² B)

= -√(1 -(-7/25) ² )

= -√(1 – (49/625))

= -√((625 – 49)/625)

= -√(576/625)

= -24/25

(i) sen(A + B)

Ya que, sen(A + B) = senA cosB + cosA senB

Asi que, 

= 5/13 x (-24/25) + (-12/13) x (-7/25)

= -120/325 + 84/325

= -36/325

(ii) cos(A + B)

Ya que, cos(A + B) = cosA cosB – senA senB

Asi que, 

= -12/13 x (-24/25) – (5/13) x (-7/25)

= 288/325 + 35/325

= 323/325

(iii) bronceado (A + B)

Ya que, tan(A + B) = sin(A + B) / cos(A + B)

Asi que, 

= (-36/325)/(323/325)

=-36/323

Pregunta 9. Demuestra que: cos 7π/12 + cos π/12 = sen 5π/12 – sen π/12

Solución:

Como sabemos que, 

7π/12 = 105°, π/12 = 15°, 5π/12 = 75°

Ahora, LHS = cos 105° + cos 15°

= coseno (90° + 15°) + sen (90° – 75°)

= -sen 15° + sen 75°

= sen 75° – sen 15°

= lado derecho

Entonces, LHS = RHS

Por lo tanto probado.

Pregunta 10. Demuestra que: (tanA + tanB) / (tanA – tanB) = sin(A + B) / sin(A – B)

Solución:

Vamos a resolver, LHS = (tanA + tanB) / (tanA – tanB)

= 

= 

Como sabemos que, 

sen(A ± B) = senA cosB ± cosA senB 

Asi que, 

= {pecado(A + B)} / {pecado(A – B)}

= lado derecho

Entonces, LHS = RHS

Por lo tanto probado.

Pregunta 11. Demostrar que:

(i) (cos 11° + sen 11°)/(cos 11° – sen 11°) = tan 56° 

(ii) (cos 9⁰+ sen 9″) / (cos 9″- sen 9°) = tan 54°

(iii) (cos 8° – sen 8°) / (cos 8° + sen 8°) = tan 37⁰

Solución:

(i) (cos 11° + sen 11°) / (cos 11° – sen 11°) = tan 56°

Vamos a resolver, LHS = (cos 11° + sen 11°)/(cos 11° – sen 11°)

Ahora dividiendo el numerador y el denominador por cos 11° obtenemos,

(cos 11° + sen 11°)/(cos 11° – sen 11°) = (1 + tan 11°)/(1 – tan 11°)

= (1+ tan 11°)/(1 – 1 x tan 11°)

= (tan 45° + tan 11°)/(1 – tan 45° x tan 11°)

Como sabemos que, 

tan(A + B) = (tanA + tanB)/(1 – tanA tanB) 

Asi que,

(bronceado 45° + bronceado 11°)/(1 – bronceado 45° x bronceado 11°) = bronceado (45° + 11°)

= bronceado 56°

= lado derecho

Entonces, LHS = RHS

Por lo tanto probado.

(ii) (cos 9° + sen 9°)/(cos 9° – sen 9°) = tan 54°

Vamos a resolver, LHS = (cos 9° + sen 9°)/(cos 9° – sen 9°)

Ahora dividiendo el numerador y el denominador por cos 9° obtenemos, 

(cos 9° + sen 9°)/(cos 9° – sen 9°) = (1 + tan 9°)/(1 – tan 9°)

= (1 + bronceado 9°) / (1 – 1 x bronceado 9°)

= (tan 45° + tan 9°)/(1 – tan 45° x tan 9°)

Como sabemos que

tan(A + B) = (tanA + tanB)/(1 – tanA tanB)

Asi que, 

(tan 45° + tan 9°)/(1 – tan 45° x tan 9°) = tan (45° + 9°)

= bronceado 54°

= lado derecho

Entonces, LHS = RHS

Por lo tanto probado.

(iii) (cos 8° – sen 8°)/(cos 8° + sen 8°) = tan 37⁰

Resolvamos, LHS = (cos 8° – sen 8°) / (cos 8° + sen 8°)

Ahora dividiendo el numerador y el denominador por cos 8° obtenemos,

(cos 8° – sen 8°) / (cos 8° + sen 8°) = (1 – tan 8°)/(1 + tan 8°) 

= (1 – tan 8°)/(1 + 1 x tan 8°)

= (bronceado 45° – bronceado 8°) / (1 + bronceado 45° x bronceado 8″)

Como sabemos que

tan(A + B) = (tanA + tanB)/(1 – tanA tanB)

Asi que,

(tan 45° – tan 8°)/(1 + tan 45° x tan 8°) = tan (45° – 8°)

= bronceado 37°

 = lado derecho

LHS = RHS

Por lo tanto probado.

Pregunta 12. Demostrar que:

(i) sen (π/3 – x) cos(π/6 + x) + cos (π/3 – x) sen(π/6 + x) = 1

(ii) sen (4π/9 + 7) cos(π/9 + 7) – cos (4π/9 + 7) sen (π/9 + 7) = √3/2

(iii) sen ( 3π/8 – 5) cos (π/8 + 5) + cos (3π/8 – 5) sen(π/8 + 5) = 1

Solución:

(i) sen (π/3 – x) cos(π/6 + x) + cos (π/3 – x) sen(π/6 + x) = 1

Vamos a resolver, LHS = sin (π/3 – x) cos(π/6 + x) + cos (π/3 – x) sin(π/6 + x)

Como sabemos que

sen(A + B) = senA cosB + cosA senB

sen (π/3 – x) cos(π/6 + x) + cos (π/3 – x) sen(π/6 + x) = sen (π/3 – x + π/6 + x)

= pecado ((2π + π)/6)

= pecado (π/2) 

= sen 90°

= 1

= lado derecho

LHS = RHS

Por lo tanto probado.

(ii) sen (4π/9 + 7) cos(π/9 + 7) – cos (4π/9 + 7) sen (π/9 + 7) = √3/2

Vamos a resolver, LHS = sin (4π/9 + 7) cos(π/9 + 7) – cos (4π/9 + 7) sin (π/9 + 7)

Como sabemos que

sen(A – B) = senA cosB – cosA senB

sen (4π/9 + 7) cos(π/9 + 7) – cos (4π/9 + 7) sen (π/9 + 7) = sen (4π/9 + 7 – π/9 – 7)

= pecado (3π/9)

= pecado (π/3)

= sen 60° 

= √3/2 

= lado derecho

LHS = RHS

Por lo tanto probado.

(iii) sen ( 3π/8 – 5) cos (π/8 + 5) + cos (3π/8 – 5) sen(π/8 + 5) = 1

Vamos a resolver, LHS = sin ( 3π/8 – 5) cos (π/8 + 5) + cos (3π/8 – 5) sin (π/8 + 5) 

Como sabemos que

sen(A + B) = senA cosB + cosA senB

sen ( 3π/8 – 5) cos (π/8 + 5) + cos (3π/8 – 5) sen(π/8 + 5) = sen (3π/8 – 5 + π/8 + 5)

= pecado ((3π + π)/8)

= pecado (4π/8)

= pecado (π/2)

= sen 90°

= 1

= lado derecho

LHS = RHS

Por lo tanto probado.

Pregunta 13. Demostrar que: (tan 69° + tan 66°)/(1 – tan 69° tan 66°) = -1

Solución:

Vamos a resolver, LHS = (tan 69°+tan 66°)/(1-tan 69° tan 66°)

Como sabemos que

tan(A + B) = (tanA + tanB) / (1 – tanA tanB)

= (tan 69° + tan 66°)/(1 – tan 69° tan 66°)

= bronceado (69 +66)°

= bronceado 135⁰

= – bronceado 45º

= -1

= lado derecho

LHS = RHS

Por lo tanto probado.

Pregunta 14. (i) Si tanA = 5/6 y tanB = 1/11, demuestre que (A + B) = π/4

(ii) Si tanA = m/(m-1) y tanB = 1/(2m – 1), entonces demuestre que (A – B) = π/4

Solución:

(yo) tenemos,

tanA = 5/6 y tanB = 1/11

Como sabemos que

tan(A + B) = (tanA + tanB)/(1 – tanA tanB)

= [(5/6) + (1/11)] /[1 – (5/6) x (1/11)]

= (55 + 6)/(66 – 5)

= 61/61

= 1

= tan 45° o tan π/4

Tan(A + B) = tan π/4

(A + B) = π/4

Por lo tanto probado.

(ii) Tenemos,

tanA = m/(m – 1) y tanB = 1/(2m – 1)

Como sabemos que

tan(A – B) = (tanA – tanB) / (1 + tanA tanB)

= 

= (2m2 ^– metro – metro + 1)/(2m2 – metro – 2m + 1 + metro ⁾

= (2m2 – 2m + 1)/(2m2 ^{– 2m +} 1)

= 1

= tan 45° o tan π/4

Tan(A – B) = tan π/4

(A – B) = π/4

Por lo tanto probado.

Pregunta 15. Demuestre que:

(i) cos ² π/4 – sen ² π/12 = √3/4 

(ii) sen ² (n + 1)A – sen ² nA = sen (2n + 1)A sen A

Solución:

(i) cos ² π/4 – sen ² π/12 = √3/4

Vamos a resolver, LHS = cos ² π/4 sen ² π/12

Como sabemos que

cos ² A – sen ² B = cos (A + B) cos (A – B)

Asi que, 

cos ² π/4 – sen ² π/12 = cos (π/4 + π/12) cos (π/4 – π/12)

= coseno 4π/12 coseno 2π/12

= cos π/3 cos π/6

= 1/2 x √3/2

= √3/4 = lado derecho

LHS = RHS 

Por lo tanto probado.

(ii) sen ² (n + 1)A – sen ² nA = sen (2n + 1)A senA

Vamos a resolver, LHS = sen ² (n+1)A – sen ² nA

Como sabemos que

sen ² A – sen ² B = sen (A + B) sen (A – B)

Donde, A = (n + 1)A y B = nA

Asi que,

sen ² (n + 1)A – sen ² nA = sen((n + 1)A + nA) sen((n + 1)A – nA)

= sen(nA + A + nA) sen (nA + A – nA)

= sen(2nA + A) senA

= sen(2n + 1)A senA 

= lado derecho

LHS = RHS

Por lo tanto probado.

Pregunta 16. Demostrar que:

(i) {sen(A + B) + sin(A – B)}/{cos(A + B) + cos(A – B)} = tanA

Solución:

Demostrar: {sen(A + B) + sin(A – B)}/{cos(A + B) + cos(A – B)} = tanA

Prueba:

Vamos a resolver, LHS = {sin(A + B) + sin(A – B)}/{cos(A + B) + cos(A – B)}

Como sabemos que, sin (A ± B) = sinA cosB ± cosA sinB y cos(A ± B) = cosA cosB ± sinA sinB

Asi que,

= 

=    

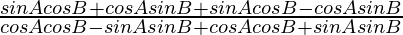
= (2cosA cosB)(2cosA cosB)

= bronceado A

= lado derecho

LHS = RHS

Por lo tanto probado.

(ii) {sen(A – B)/cosA.cosB} + {sen(B – C)/cosB.cosC} + {sen(C – A)/cosC.cosA} = 0

Solución:

Demostrar: {sen(A – B)/cosA.cosB} + {sen(B – C)/cosB.cosC} + {sen(C – A)/cosC.cosA} = 0

Prueba:

Vamos a resolver, LHS = {sin(A – B)/cosA.cosB} + {sin(B – C)/cosB.cosC} + {sin(C – A)/cosC.cosA}

Como sabemos que

sen(A – B) = senA cosB – cosA senB

Asi que, 

= {sen(A – B)/cosA.cosB} + {sen(B – C)/cosB.cosC} + {sen(C – A)/cosC.cosA}

= (senA cosB – cosA senB)/(cosA cosB) + (senB cosC – cosB senC)/(cosB cosC) + 

   (sinC cosA – cosC sinA)/(cosC cosA)

= (senA cosB)/(cosA senB) – (cosA senB)/(cosB cosC) + (senB cosC)/(cosB cosC) – 

  (cosB sinC)/(cosB cosC) + (sinC cosA)/(cosC cosA)

= tanA – tanB + tanB – tanC+ tanC – tanA

= 0

= lado derecho

LHS = RHS

Por lo tanto probado.

(iii) {sin(A – B)/sinA.sinB} + {sin(B – C)/sinB.sinC} + {sin(C – A)/sinC.sinA} = 0

Solución:

Demostrar: {sin(A – B)/sinA.sinB} + {sin(B – C)/sinB.sinC} + {sin(C – A)/sinC.sinA} = 0

Prueba:

Vamos a resolver, LHS = {sin(A – B)/sinA.sinB} + {sin(B – C)/sinB.sinC} + {sin(C – A)/sinC.sinA}

Como sabemos que

sen(A – B) = senA cosB – cosA senB

= {sen(A – B)/senA.senB} + {sen(B – C)/senB.senC} + {sen(C – A)/senC.senA}

= (sinA cosB – cosA sinB)/(sinA sinB) + (sinB cosC – cosB sinC)/(sinB sinC) + 

    (sinC cosA- cosC sinA)/(sinC sinA)

= (senA.cosB)/(senA.senB) – (cosA.senB)/(senA.senB) + (senB.cosC)/(senB.senC) – 

   (cosB.sinC)/(sinB.sinC) +(sinC.cosA)/(sinC.sinA) – (cosC.sinA)/(sinC.sinA)

= cunaB – cunaA + cunaC – cunaB + cunaA – cuna C

= 0

= lado derecho

LHS = RHS

Por lo tanto probado.

(iv) sen ² B = sen ² A + sen ² (A – B) – 2 sen A cos B sen (A – B)

Solución:

Demostrar: sen ² B = sen ² A + sen ² (A – B) – 2 sen A cosB sen (A – B)

Prueba:

Resolvamos RHS = sin ² A + sin ² (A – B) – 2 sinA cosB sin(A – B)

= sen ² A+ sen(A -B)[sen(A – B) – 2 senA cosB]

Como sabemos que

sen(A – B) = senA cosB – cosA senB

Asi que,

= sen ² A + sen (A -B) [ senA cosB – cosA senB – 2 senA cosB]

= sen ² A + sen (AB) [- sen A cos B – cos A sen B] 

= sen ² A – sen (A -B) [ sen A cos B + cos A sen B]

Como sabemos que

sen (A +B) = sen A cos B + cos A sen B 

Asi que,

= sen ² A – sen(A – B) sen(A + B).

= sen ² A – sen ² A + sen ² B

= sen ² B

= LHS

LHS = RHS

Por lo tanto probado.

(v) cos ² A + cos ² B – 2 cos A cos B cos (A + B) = sen ² (A + B)

Solución:

Demostrar: cos ² A + cos ² B – 2 cosA cosB cos(A + B) = sen ² (A + B)

Prueba:

Resolvemos LHS = cos ² A + cos ² B – 2 cosA cosB cos(A + B)

= cos ² A + 1 – sen ² B – 2 cos A cos B cos (A + B)

= 1 + cos ² A – sen ² B – 2 cos A cos B cos (A + B)

Como sabemos que cos ² A – sen ² B = cos(A + B) cos(A – B)

Asi que,

= 1 + cos(A + B) cos(A – B) – 2 cosA cosB cos(A + B)

= 1 + cos(A + B)[cos(A – B) – 2 cosA cosB]

También, 

cos(A – B) = cosA cosB + senA senB

Asi que,

= 1 + cos(A +B)[cosA cosB + senA senB – 2 cosA cosB]

= 1 + cos(A +B)[-cosA cosB + senA senB]

= 1 cos(A +B)[cosA cosB – senA senB]

También,

cos(A + B) = cosA cosB – senA senB

Asi que,

1 – cos ² (A + B) = sen ² (A + B) = lado derecho

LHS = RHS

Por lo tanto probado.

(vi) tan(A + B)/cot(A – B) = (tan ² A – tan ² B)/(1 – tan ² A tan ² B)

Solución:

Demostrar: tan(A + B)/cot(A – B) = (tan ² A – tan ² B)/(1 – tan ² A tan ² B)

Prueba:

Resolvemos LHS = tan(A + B)/cot(A – B)

Como sabemos que

tan (A ± B) = (tanA ± tanB) / (1 ± tanA tanB)

Asi que, 

 

= 

Sabemos que, (x+y) (x – y) = x ² – y ²

Asi que,

 

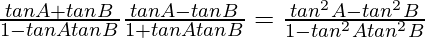
= lado derecho

LHS = RHS 

Por lo tanto probado.