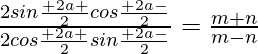Pregunta 11. Si cosec A + sec A = cosec B + sec B, demuestre que tan A tan B = 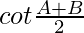 .
.
Solución:
Tenemos, cosec A + sec A = cosec B + sec B
=> segundo A − segundo segundo = segundo segundo − segundo segundo
=>
=>
=>
=> bronceado A bronceado B =
=> bronceado A bronceado B =
Por lo tanto probado.
Pregunta 12. Si sen 2A = λ sen 2B, demuestre que 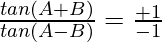 .
.
Solución:
Nos dan, sen 2A = λ sen 2B
=>
Aplicando Componendo y Dividendo se obtiene,
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 13. Demostrar que:
(i) 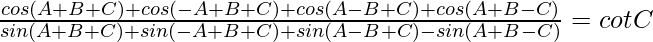
Solución:
Tenemos,
IZQ =
=
=
=
=
=
=
=
= cuna C
= lado derecho
Por lo tanto probado.
(ii) sen (B−C) cos (A−D) + sen (C−A) cos (B−D) + sen (A−B) cos (C−D) = 0
Solución:
Tenemos, LHS = sen (B−C) cos (A−D) + sen (C−A) cos (B−D) + sen (A−B) cos (C−D)
=
=
=
=
= 0
= lado derecho
Por lo tanto probado.
Pregunta 14. Si 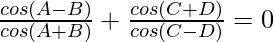 , demuestre que tan A tan B tan C tan D = −1.
, demuestre que tan A tan B tan C tan D = −1.
Solución:
Tenemos,
=>
=>
=>
=>
=>
=>
=>
=>
. . . . (1)
También,
=>
=>
=>
=>
=>
. . . . (2)
Dividiendo (1) por (2), obtenemos,
=>
=>
=>
=> tan A tan B tan C tan D = −1
Por lo tanto probado.
Pregunta 15. Si cos ( α+β) sin(γ+δ) = cos (α−β) sin(γ−δ), demuestre que cot α cot β cot γ = cot δ.
Solución:
Tenemos, cos (α+β) sen(γ+δ) = cos (α−β) sen(γ−δ)
=>
=>
=>
=>
=>
. . . . (1)
También,
=>
=>
=>
=>
. . . . (2)
Dividiendo (1) por (2), obtenemos,
=>
=>
=> cuna α cuna β = tan γ cuna δ
=> cuna α cuna β cuna γ = cuna δ
Por lo tanto probado.
Pregunta 16. Si y sen Ø = x sen (2 θ + Ø), demuestre que (x + y) cot ( θ + Ø) = (y − x) cot θ.
Solución:
Dado, y sen Ø = x sen (2θ + Ø)
=>
Aplicando Componendo y Dividendo se obtiene,
=>
=>
=>
=>
=> tan (Ø+θ) cot θ =
=>
=> (y − x) cuna θ = (x + y) cuna (θ + Ø)
=> (x + y) cuna (θ + Ø) = (y − x) cuna θ
Por lo tanto probado.
Pregunta 17. Si cos (A+B) sen (C − D) = cos (A−B) sen (C+D), demuestre que tan A tan B tan C+ tan D = 0.
Solución:
Nos dan, cos (A+B) sen (C−D) = cos (A−B) sen (C+D)
=>
Aplicando Componendo y Dividendo se obtiene,
=>
=>
=>
=>
=> −tan D = tan A tan B tan C
=> tan A tan B tan C+ tan D = 0
Por lo tanto probado.
Pregunta 18. Si 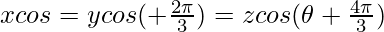 , prueba que xy + yz + zx = 0.
, prueba que xy + yz + zx = 0.
Solución:
Tenemos,
= k (digamos)
x =
y =
z =
Entonces, LHS = xy + yz + zx
=
=
=
=
=
=
= 0
= lado derecho
Por lo tanto probado.
Pregunta 19. Si m sen θ = n sen ( θ + 2a), demuestre que  .
.
Solución:
Nos dan, m sen θ = n sen (θ + 2a)
=>
Aplicando Componendo y Dividendo se obtiene,
=>
=>
=>
=>
=>
Por lo tanto, probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA


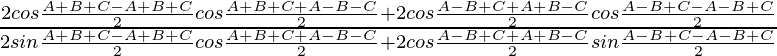

![Rendered by QuickLaTeX.com \frac{1}{2}[sin(B−C+A-D)+sin(B−C-A+D)+sin(C−A+B-D)+sin(C-A-B+D)+sin(A−B+C-D)+sin(A-B-C+D)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-01968bbbcc3faa38ed801c0f505d39d7_l3.png)
![Rendered by QuickLaTeX.com \frac{1}{2}[sin(A+B−C-D)-sin(A+C-B-D)-sin(A+D-B-C)-sin(A+B-C-D)+sin(A+C−B-D)+sin(A+D-B-C)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0874d0183d99c72eb3e8db6358494780_l3.png)
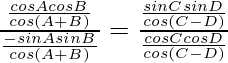
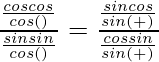
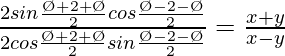
![Rendered by QuickLaTeX.com k^2\left[\frac{1}{cos\theta cos(\theta+\frac{2\pi}{3})}+\frac{1}{cos(\theta+\frac{2\pi}{3}) cos(\theta+\frac{4\pi}{3})}+\frac{1}{cos\theta cos(\theta+\frac{4\pi}{3})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a8eab68c4664758098153e16492be091_l3.png)
![Rendered by QuickLaTeX.com k^2\left[\frac{cos(\theta+\frac{4\pi}{3})+cos\theta +cos(\theta+\frac{2\pi}{3})}{cos\theta cos(\theta+\frac{2\pi}{3})cos(\theta+\frac{4\pi}{3})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d8e833292aff47d77ceb266714242f26_l3.png)
![Rendered by QuickLaTeX.com k^2\left[\frac{cos\theta cos\frac{4\pi}{3}-sin\theta sin\frac{4\pi}{3}+cos\theta +cos\theta cos\frac{2\pi}{3}-sin\theta sin\frac{2\pi}{3}}{cos\theta cos(\theta+\frac{2\pi}{3})cos(\theta+\frac{4\pi}{3})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52b1c56e816fe8234ad95d78b994a590_l3.png)
![Rendered by QuickLaTeX.com k^2\left[\frac{cos\theta(\frac{-1}{2})-sin\theta(\frac{-\sqrt{3}}{2})+cos\theta +cos\theta (\frac{-1}{2})-sin\theta (\frac{\sqrt{3}}{2})}{cos\theta cos(\theta+\frac{2\pi}{3})cos(\theta+\frac{4\pi}{3})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-26cd5a0f2ae49128371f8abd010cd4c8_l3.png)
![Rendered by QuickLaTeX.com k^2\left[\frac{-cos\theta+sin\theta(\frac{\sqrt{3}}{2})+cos\theta -sin\theta (\frac{\sqrt{3}}{2})}{cos\theta cos(\theta+\frac{2\pi}{3})cos(\theta+\frac{4\pi}{3})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cbfa2dfeace9590becfc360f8ca53709_l3.png)
![Rendered by QuickLaTeX.com k^2\left[\frac{0}{cos\theta cos(\theta+\frac{2\pi}{3})cos(\theta+\frac{4\pi}{3})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bfe1ffd69f291c0dcc30df52dd683e63_l3.png)