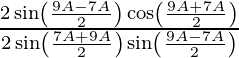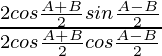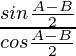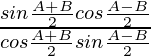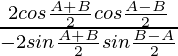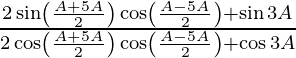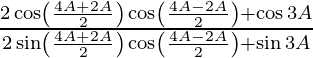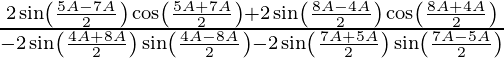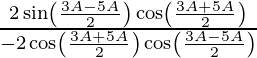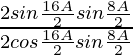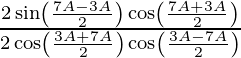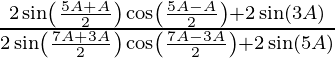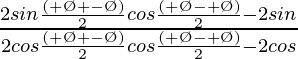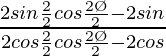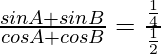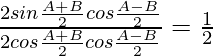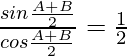Pregunta 1. Exprese cada uno de los siguientes como el producto de senos y cosenos:
(i) sen 12θ + sen 4θ
Solución:
Sabemos, sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2
sen 12θ + sen 4θ = 2 sen (12θ + 4θ)/2 coseno (12θ – 4θ)/2
= 2 sen 16θ/2 cos 8θ/2
= 2 sen 8θ cos 4θ
(ii) sen 5 θ – sen θ
Solución:
Sabemos, sen A – sen B = 2 cos (A+B)/2 sen (A–B)/2
sen 5θ – sen θ = 2 cos (5θ + θ)/2 sen (5θ – θ)/2
= 2 cos 6θ/2 sen 4θ/2
= 2 cos 3θ sen 2θ
(iii) cos 12θ + cos 8θ
Solución:
Sabemos, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
coseno 12θ + coseno 8θ = 2 coseno (12θ + 8θ)/2 coseno (12θ – 8θ)/2
= 2 cos 20θ/2 cos 4θ/2
= 2 cos 10θ cos 2θ
(iv) cos 12θ – cos 4θ
Solución:
Sabemos, cos A – cos B = –2 sen (A+B)/2 sen (A–B)/2
cos 12θ – cos 4θ = –2 sen (12θ + 4θ)/2 sen (12θ – 4θ)/2
= –2 sen 16θ/2 sen 8θ/2
= –2 sen 8θ sen 4θ
(v) sen 2θ + cos 4θ
Solución:
sen 2θ + cos 4θ = sen 2θ + sen (90 o – 4θ)
Sabemos, sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2
sen 2θ + sen (90 o – 4θ) = 2 sen (2x + 90 o – 4θ)/2 cos (2θ – 90 o + 4θ)/2
= 2 sen (90 ° – 2θ)/2 coseno (6θ – 90 ° )/2
= 2 sen (45 o – θ) cos (3θ – 45 o )
= 2 sen (45 o – θ) cos [–(45 o – 3θ)]
= 2 sen (45 o – θ) cos (45 o – 3θ)
= 2 sen (π/4 – θ) cos (π/4 – 3θ)
Pregunta 2. Demuestra que:
(i) sen 38° + sen 22° = sen 82°
Solución:
Dado, LHS = sen 38° + sen 22°.
Sabemos, sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2
sen 38° + sen 22° = 2 sen (38 o + 22 o )/2 cos (38 o – 22 o )/2
= 2 sen 60 o /2 cos 16 o /2
= 2 sen 30 o cos 8 o
= 2 × (1/2) × cos 8 o
= cos 8 o
= coseno (90° – 82°)
= sen 82°
= lado derecho
Por lo tanto probado.
(ii) cos 100° + cos 20° = cos 40°
Solución:
Dado, LHS = cos 100° + cos 20°.
Sabemos, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos 100° + cos 20° = 2 cos (100 o + 20 o )/2 cos (100 o – 20 o )/2
= 2 cos 120 o /2 cos 80 o /2
= 2 cos 60 o cos 40 o
= 2 × (1/2) × cos 40 o
= cos 40 o
= lado derecho
Por lo tanto Probado.
(iii) sen 50° + sen 10° = cos 20°
Solución:
Dado, LHS = sen 50° + sen 10°.
Sabemos que sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2.
sen 50° + sen 10° = 2 sen (50 o + 10 o )/2 cos (50 o – 10 o )/2
= 2 sen 60 o /2 cos 40 o /2
= 2 sen 30 o cos 20 o
= 2 × (1/2) × cos 20 o
= cos 20 o
= lado derecho
Por lo tanto Probado.
(iv) sen 23° + sen 37° = cos 7°
Solución:
Dado LHS = sen 23° + sen 37°.
Sabemos que sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2
sen 23° + sen 37° = 2 sen (23 o + 37 o )/2 cos (23 o – 37 o )/2
= 2 sen 60 o /2 coseno (–14 o /2)
= 2 sen 30 o cos (–7 o )
= 2 × (1/2) × cos 7 o
= cos 7 o
= lado derecho
Por lo tanto Probado.
(v) sen 105° + cos 105° = cos 45°
Solución:
Dado, LHS = sin 105° + cos 105°
sen 105° + cos 105° = sen 105 o + sen (90 o – 105 o )
= sen 105 o + sen (–15 o )
= sen 105 o – sen 15 o
Sabemos, sen A – sen B = 2 cos (A+B)/2 sen (A–B)/2
sen 105 o – sen 15 o = 2 cos (105 o + 15 o )/2 sen (105 o – 15 o )/2
= 2 cos 120 o /2 sen 90 o /2
= 2 cos 60 o sen 45 o
= 2 × (1/2) × (1/√2)
= 1/√2
= cos 45 o
= lado derecho
Por lo tanto Probado.
(vi) sen 40° + sen 20° = cos 10°
Solución:
Dado, LHS = sen 40° + sen 20°.
Sabemos, sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2
sen 40° + sen 20° = 2 sen (40 o + 20 o )/2 cos (40 o – 20 o )/2
= 2 sen 60 o /2 cos 20 o /2
= 2 sen 30 o cos 10 o
= 2 × (1/2) × cos 10 o
= cos 10 o
= lado derecho
Por lo tanto Probado.
Pregunta 3. Demuestra que:
(i) cos 55° + cos 65° + cos 175° = 0
Solución:
Dado, LHS = cos 55° + cos 65° + cos 175°.
Sabemos, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos 55° + cos 65° + cos 175° = 2 cos (55 o + 65 o )/2 cos (55 o – 65 o ) + cos (180 o – 5 o )
= 2 cos 120 o /2 cos (–10o)/2 – cos 5 o
= 2 cos 60° cos (–5°) – cos 5°
= 2 × (1/2) × cos 5 o – cos 5 o
= cos 5 o – cos 5 o
= 0
= lado derecho
Por lo tanto Probado.
(ii) sen 50° – sen 70° + sen 10° = 0
Solución:
Dado, LHS = sen 50° – sen 70° + sen 10°.
Sabemos, sen A – sen B = 2 cos (A+B)/2 sen (A–B)/2
sen 50° – sen 70° + sen 10° = 2 cos (50 o + 70 o )/2 sen (50 o – 70 o ) + sen 10 o
= 2 cos 120 o /2 sen (–20 o )/2 + sen 10 o
= 2 cos 60 o (–sen 10 o ) + sen 10 o
= 2 × (1/2) × (–sen 10 o ) + sen 10 o
= 0
= lado derecho
Por lo tanto Probado.
(iii) cos 80° + cos 40° – cos 20° = 0
Solución:
Dado LHS = cos 80° + cos 40° – cos 20°.
Sabemos, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos 80° + cos 40° – cos 20° = 2 cos (80 o + 40 o )/2 cos (80 o – 40 o ) – cos 20 o
= 2 cos 120 o /2 cos 40 o /2 – cos 20 o
= 2 cos 60° cos 20 o – cos 20°
= 2 × (1/2) × cos 20 o – cos 20 o
= 0
= lado derecho
Por lo tanto Probado.
(iv) cos 20° + cos 100° + cos 140° = 0
Solución:
Dado, LHS = cos 20° + cos 100° + cos 140°.
Sabemos, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2.
cos 20° + cos 100° + cos 140° = 2 cos (20 o + 100 o )/2 cos (20 o – 100 o ) + cos (80 o – 40 o )
= 2 cos 120 o /2 cos (–80 o )/2 – cos 40 o
= 2 cos 60° cos (–40°) – cos 40°
= 2 × (1/2) × cos 40 o – cos 40 o
= 0
= lado derecho
Por lo tanto Probado.
(v) sen 5π/18 – cos 4π/9 = √3 sen π/9
Solución:
Dado, LHS = sin 5π/18 – cos 4π/9
= sen 5π/18 – sen (π/2 – 4π/9)
= sen 5π/18 – sen (9π – 8π)/18
= sen 5π/18 – sen π/18
Sabemos, sen A – sen B = 2 cos (A+B)/2 sen (A– B)/2
= 2 coseno (6π/36) sen (4π/36)
= 2 cos π/6 sen π/9
= 2 cos 30 o sen π/9
= 2 × (√3/2) × sen π/9
= √3 sen π/9
= lado derecho
Por lo tanto Probado.
(vi) cos π/12 – sen π/12 = 1/√2
Solución:
Dado, cos π/12 – sen π/12 = sen (π/2 – π/12) – sen π/12
= sen (6π – 5π)/12 – sen π/12
= sen 5π/12 – sen π/12
Sabemos, sen A – sen B = 2 cos (A+B)/2 sen (A–B)/2
= 2 coseno (6π/24) sen (4π/24)
= 2 cos π/4 sen π/6
= 2 cos 45 o sen 30 o
= 2 × (1/√2) × (1/2)
= 1/√2
= lado derecho
Por lo tanto Probado.
(vii) sen 80° – cos 70° = cos 50°
Solución:
Tenemos, sen 80° = cos 50° + cos 70 o
Aquí, RHS = cos 50° + cos 70 o
Sabemos,
cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos 50° + cos 70 o = 2 cos (50 o + 70 o )/2 cos (50 o – 70 o )/2
= 2 cos 120 o /2 cos (–20 o )/2
= 2 cos 60 o cos (–10 o )
= 2 × (1/2) × cos 10 o
= cos 10 o
= coseno (90° – 80°)
= sen 80°
= LHS
Por lo tanto Probado.
(viii) sen 51° + cos 81° = cos 21°
Solución:
Dado, LHS = sen 51° + cos 81°
= sen 51 o + sen (90 o – 81 o )
= sen 51 o + sen 9 o
Sabemos, sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2
sen 51 o + sen 9 o = 2 sen (51 o + 9 o )/2 cos (51 o – 9 o )/2
= 2 sen 60 o /2 cos 42 o /2
= 2 sen 30 o cos 21 o
= 2 × (1/2) × cos 21 o
= cos 21 o
= lado derecho
Por lo tanto Probado.
Pregunta 4. Demuestra que:
(i) cos (3π/4 + x) – cos (3π/4 – x) = –√2 sen x
Solución:
Dado, LHS = cos (3π/4 + x) – cos (3π/4 – x)
Sabemos, cos A – cos B = –2 sen (A+B)/2 sen (A–B)/2
cos (3π/4 + x) – cos (3π/4 – x) = –2 sen (3π/4 + x + 3π/4 – x)/2 sen (3π/4 + x – 3π/4 + x) /2
= –2 sen (6π/4)/2 sen 2x/2
= –2 sen 6π/8 sen x
= –2 sen 3π/4 sen x
= –2 sen (π – π/4) sen x
= –2 sen π/4 sen x
= –2 × (1/√2) × sen x
= –√2 sen x
= lado derecho
Por lo tanto probado.
(ii) cos (π/4 + x) + cos (π/4 – x) = √2 cos x
Solución:
Dado, LHS = cos (π/4 + x) + cos (π/4 – x)
Sabemos, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
coseno (π/4 + x) + coseno (π/4 – x) = 2 coseno (π/4 + x + π/4 – x)/2 coseno (π/4 + x – π/4 + x)/ 2
= 2 porque (2π/4)/2 porque 2x/2
= 2 cos 2π/8 cos x
= 2 sen π/4 cos x
= 2 × (1/√2) × cos x
= √2 cos x
= lado derecho
Por lo tanto probado.
Pregunta 5. Demuestre que:
(i) sen 65 o + cos 65 o = √2 cos 20 o
Solución:
Dado LHS = sen 65 o + cos 65 o
= sen 65 o + sen (90 o – 65 o )
= sen 65 o + sen 25 o
Sabemos, sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2
sen 65 o + sen 25 o = 2 sen (65 o + 25 o )/2 cos (65 o – 25 o )/2
= 2 sen 90 o /2 cos 40 o /2
= 2 sen 45 o cos 20 o
= 2 × (1/√2) × cos 20 o
= √2 cos 20 o
= lado derecho
Por lo tanto probado.
(ii) sen 47 o + cos 77 o = cos 17 o
Solución:
Dado, LHS = sen 47 o + cos 77 o
= sen 47 o + sen (90 o – 77 o )
= sen 47 o + sen 13 o
Sabemos, sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2
sen 47 o + sen 13 o = 2 sen (47 o + 13 o )/2 cos (47 o – 13 o )/2
= 2 sen 60 o /2 cos 34 o /2
= 2 sen 30 o cos 17 o
= 2 × (1/2) × cos 17 o
= cos 17 o
= lado derecho
Por lo tanto probado.
Pregunta 6. Demuestra que:
(i) cos 3A + cos 5A + cos 7A + cos 15A = 4 cos 4A cos 5A cos 6A
Solución:
Dado, LHS = cos 3A + cos 5A + cos 7A + cos 15A
= (cos 5A + cos 3A) + (cos 15A + cos 7A)
Sabemos, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
= (cos 5A + cos 3A) + (cos 15A + cos 7A)
= [2 cos (5A+3A)/2 cos (5A–3A)/2] + [2 cos (15A+7A)/2 cos (15A–7A)/2]
= [2 cos 8A/2 cos 2A/2] + [2 cos 22A/2 cos 8A/2]
= [2 cos 4A cos A] + [2 cos 11A cos 4A]
= 2 cos 4A (cos 11A + cos A)
= 2 cos 4A [2 cos (11A+A)/2 cos (11A-A)/2]
= 2 cos 4A [2 cos 12A/2 cos 10A/2]
= 2 cos 4A [2 cos 6A cos 5A]
= 4 cos 4A cos 5A cos 6A
= lado derecho
Por lo tanto probado.
(ii) cos A + cos 3A + cos 5A + cos 7A = 4 cos A cos 2A cos 4A
Solución:
Dado LHS = cos A + cos 3A + cos 5A + cos 7A
= (cos 3A + cos A) + (cos 7A + cos 5A)
Sabemos, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
= (cos 3A + cos A) + (cos 7A + cos 5A)
= [2 cos (3A+A)/2 cos (3A–A)/2] + [2 cos (7A+5A)/2 cos (7A–5A)/2]
= [2 cos 4A/2 cos 2A/2] + [2 cos 12A/2 cos 2A/2]
= [2 cos 2A cos A] + [2 cos 6A cos A]
= 2 cos A (cos 6A + cos 2A)
= 2 cos A [2 cos (6A+2A)/2 cos (6A–2A)/2]
= 2 cos A [2 cos 8A/2 cos 4A/2]
= 2 cos A [2 cos 4A cos 2A]
= 4 cos A cos 2A cos 4A
= lado derecho
Por lo tanto probado.
(iii) sen A + sen 2A + sen 4A + sen 5A = 4 cos A/2 cos 3A/2 sen 3A
Solución:
Dado, LHS = sen A + sen 2A + sen 4A + sen 5A
= (sen 2A + sen A) + (sen 5A + sen 4A)
Sabemos, sen A + sen B = 2 sen (A+B)/2 cos (A–B)/2
= (sen 2A + sen A) + (sen 5A + sen 4A)
= [2 sen (2A+A)/2 cos (2A–A)/2] + [2 sen (5A+4A)/2 cos (5A–4A)/2]
= [2 sen 3A/2 cos A/2] + [2 sen 9A/2 cos A/2]
= 2 cos A/2 (sen 9A/2 + sen 3A/2)
= 2 cos A/2 [2 sen (9A/2 + 3A/2)/2 cos (9A/2 – 3A/2)/2]
= 2 cos A/2 [2 sen ((9A+3A)/2)/2 cos ((9A–3A)/2)/2]
= 2 cos A/2 [2 sen 12A/4 cos 6A/4]
= 2 cos A/2 [2 sen 3A cos 3A/2]
= 4 cos A/2 cos 3A/2 sen 3A
= lado derecho
Por lo tanto probado.
(iv) sen 3A + sen 2A – sen A = 4 sen A cos A/2 cos 3A/2
Solución:
Dado, LHS = sen 3A + sen 2A – sen A
= (sen 3A – sen A) + sen 2A
Sabemos, sen A – sen B = 2 cos (A+B)/2 sen (A–B)/2
= (sen 3A – sen A) + sen 2A
= 2 coseno (3A + A)/2 sen (3A – A)/2 + sen 2A
= 2 cos 4A/2 sen 2A/2 + sen 2A
= 2 cos 2A sen A + 2 sen A cos A
= 2 sen A (cos 2A + cos A)
= 2 sen A [2 cos (2A+A)/2 cos (2A-A)/2]
= 2 sen A [2 cos 3A/2 cos A/2]
= 4 sen A cos A/2 cos 3A/2
= lado derecho
Por lo tanto probado.
(v) cos 20 o cos 100 o + cos 100 o cos 140 o – cos 140 o cos 200 o = – 3/4
Solución:
Dado LHS = cos 20 o cos 100 o + cos 100 o cos 140 o – cos 140 o cos 200 o
= 1/2 [2 cos 100 o cos 20 o + 2 cos 140 o cos 100 o – 2 cos 200 o cos 140 o ]
Sabemos que, 2 cos A cos B = cos (A+B) + cos (A–B)
= 1/2 [cos (100 o + 20 o ) + cos (100 o – 20 o ) + cos (140 o + 100 o ) + cos (140 o – 100 o ) – cos (200 o + 140 o ) – porque (200 o – 140 o )]]
= 1/2 [cos 120 o + cos 80 o + cos 240 o + cos 40 o – cos 340 o – cos 60 o ]
= 1/2 [cos (90 o + 30 o ) + cos 80 o + cos (180 o + 60 o ) + cos 40 o – cos (360 o – 20 o ) – cos 60 o ]
= 1/2 [–sen 30 o + cos 80 o – cos 60 o + cos 40 o – cos 20 o – cos 60 o ]
= 1/2 [–sen 30 o + cos 80 o + cos 40 o – cos 20 o – 2 cos 60 o ]
= 1/2 [–sen 30 o + 2 cos (80 o +40 o )/2 cos (80 o –40 o )/2 – cos 20 o – 2 × 1/2]
= 1/2 [–sen 30 o + 2 cos 120 o /2 cos 40 o /2 – cos 20 o – 1]
= 1/2 [–sen 30 o + 2 cos 60 o cos 20 o – cos 20 o – 1]
= 1/2 [–1/2 + 2×(1/2)×cos 20 o – cos 20 o – 1]
= 1/2 [–1/2 + cos 20 o – cos 20 o – 1]
= 1/2 [–1/2 –1]
= 1/2 [–3/2]
= –3/4
= lado derecho
Por lo tanto probado.
(vi) sen x/2 sen 7x/2 + sen 3x/2 sen 11x/2 = sen 2x sen 5x
Solución:
Dado LHS = sen x/2 sen 7x/2 + sen 3x/2 sen 11x/2
= 1/2 [2 sen 7x/2 sen x/2 + 2 sen 11x/2 sen 3x/2]
Sabemos, 2 sen A sen B = cos (A–B) – cos (A+B)
= 1/2 [cos (7x/2 – x/2) – cos (7x/2 + x/2) + cos (11x/2 – 3x/2) – cos (11x/2 + 3x/2)]
= 1/2 [cos (7x–x)/2 – cos (7x+x)/2 + cos (11x–3x)/2 – cos (11x+3x)/2]
= 1/2 [cos 6x/2 – cos 8x/2 + cos 8x/2 – cos 14x/2]
= 1/2 [cos 3x – cos 7x]
= –1/2 [cos 7x – cos 3x]
= –1/2 [–2 sen (7x+3x)/2 sen (7x–3x)/2]
= –1/2 [–2 sen 10x/2 sen 4x/2]
= –1/2 [–2 sen 5x sen 2x]
= –2/–2 sen 5x sen 2x
= sen 2x sen 5x
= lado derecho
Por lo tanto probado.
(vii) cos x cos x/2 – cos 3x cos 9x/2 = sen 4x sen 7x/2
Solución:
Dado LHS = cos x cos x/2 – cos 3x cos 9x/2
= 1/2 [2 cos x cos x/2 – 2 cos 9x/2 cos 3x]
Sabemos, 2 cos A cos B = cos (A+B) + cos (A–B)
= 1/2 [cos (x + x/2) + cos (x – x/2) – cos (9x/2 + 3x) – cos (9x/2 – 3x)]
= 1/2 [cos (2x+x)/2 + cos (2x–x)/2 – cos (9x+6x)/2 – cos (9x–6x)/2]
= 1/2 [cos 3x/2 + cos x/2 – cos 15x/2 – cos 3x/2]
= 1/2 [cos x/2 – cos 15x/2]
= – 1/2 [cos 15x/2 – cos x/2]
= – 1/2 [–2 sen (15x/2 + x/2)/2 sen (15x/2 – x/2)/2]
= -1/2 [–2 sen (16x/2)/2 sen (14x/2)/2]
= -1/2 [–2 sen 16x/4 sen 7x/2]
= – 1/2 [–2 sen 4x sen 7x/2]
= –2/–2 [sen 4x sin 7x/2]
= sen 4x sen 7x/2
= lado derecho
Por lo tanto probado.
Pregunta 7. Demuestra que:
(i) 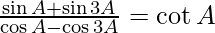
Solución:
Tenemos,
IZQ =
=
=
=
= cuna A
= lado derecho
Por lo tanto probado.
(ii) 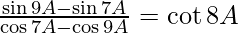
Solución:
Tenemos,
IZQ =
=
=
= cuna 8A
= lado derecho
Por lo tanto probado.
(iii)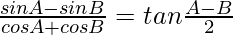
Solución:
Tenemos,
IZQ =
=
=
=
= lado derecho
Por lo tanto probado.
(iv)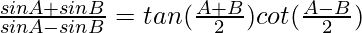
Solución:
Tenemos,
IZQ =
=
=
=
= lado derecho
Por lo tanto probado.
(iv)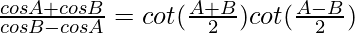
Solución:
Tenemos,
IZQ =
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 8. Demuestre que:
(i) 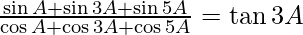
Solución:
Tenemos,
IZQ =
=
=
=
=
=
= bronceado 3A
= lado derecho
Por lo tanto probado.
(ii)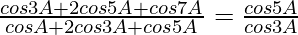
Solución:
Tenemos,
IZQ =
=
=
=
=
= lado derecho
Por lo tanto probado.
(iii) 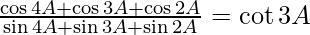
Solución:
Tenemos,
IZQ =
=
=
=
=
= cuna 3A
= lado derecho
Por lo tanto probado.
(iv) 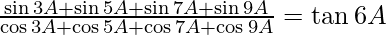
Solución:
Tenemos,
IZQ =
=
=
=
=
=
= bronceado 6A
= lado derecho
Por lo tanto probado.
(v) 
Solución:
Tenemos,
IZQ =
=
=
=
=
=
= cuna 6A
= lado derecho
Por lo tanto probado.
(vi) 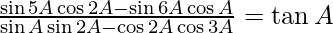
Solución:
Tenemos,
IZQ =
Multiplicando numerador y denominador por 2, obtenemos
=
=
=
=
=
=
=
=
=
= bronceado A
= lado derecho
Por lo tanto probado.
(vii)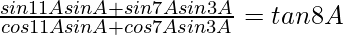
Solución:
Tenemos,
IZQ =
=
=
=
=
= bronceado 8A
= lado derecho
Por lo tanto probado.
(viii) 
Solución:
Tenemos,
IZQ =
Al multiplicar el numerador y el denominador por 2, obtenemos
=
=
=
=
=
=
=
=
= bronceado 2A
= lado derecho
Por lo tanto probado.
(ix) 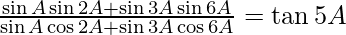
Solución:
Tenemos,
IZQ =
Al multiplicar el numerador y el denominador por 2, obtenemos
=
=
=
=
=
=
=
= bronceado 5A
= lado derecho
Por lo tanto probado.
(X) 
Solución:
Tenemos,
IZQ =
=
=
=
=
= sen3A/sen5A
= lado derecho
Por lo tanto probado.
(xi)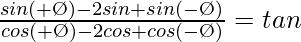
Solución:
Tenemos,
IZQ =
=
=
=
=
=
=
= bronceado θ
= lado derecho
Por lo tanto probado.
Pregunta 9. Demostrar que:
(i) sen α + sen β + sen γ – sen (α + β + γ) = 4 sen (α + β)/2 sen (β + γ)/2 sen (α + γ)/2
Solución:
Tenemos,
LHS = sen α + sen β + sen γ – sen (α + β + γ)
=
=
=
=
=
=
= 4 sen (α + β)/2 sen (β + γ)/2 sen (α + γ)/2
= lado derecho
Por lo tanto probado.
(ii) cos (A + B + C) + cos (A – B + C) + cos (A + B – C) + cos (–A + B + C) = 4 cos A cos B cos C
Solución:
Tenemos,
LHS = coseno (A + B + C) + coseno (A – B + C) + coseno (A + B – C) + coseno (–A + B + C)
=
=
= 2 coseno (A + C) coseno B + 2 coseno B coseno (A − C)
= 2 cos B [cos (A + C) + cos (A − C)]
= 2 cos B
= 2 cos B [2 cos A cos C]
= 4 cos A cos B cos C
= lado derecho
Por lo tanto probado.
Pregunta 10. Si cos A + cos B = 1/2 y sen A + sen B = 1/4, prueba que 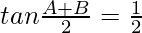 .
.
Solución:
Tenemos,
cos A + cos B = 1/2
sen A + sen B = 1/4
=>
=>
=>
=>
=>
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA