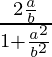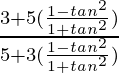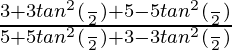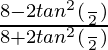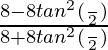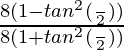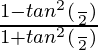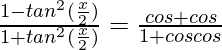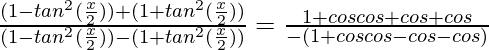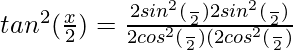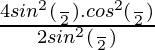Pregunta 30(i). Si 0 ≤ x≤ π y x se encuentra en el segundo cuadrante tal que senx = 1/4, encuentre los valores de cos(x/2), sen(x/2) y tan(x/2).
Solución:
Dado que,
senx = 1/4
Como sabemos, senx = √(1 – cos 2 x)
Asi que,
⇒ (1/4) 2 = (1 – porque 2 x)
⇒ (1/16) – 1 = – porque 2 x
cos x = ± √15/4
Se da que x está en el segundo cuadrante, por lo que cosx es negativo.
cos x = – √15/4
Ahora,
Como sabemos que, cosx = 2 cos 2 (x/2) – 1
Asi que,
⇒ – √15/4 = 2cos 2 (x/2) – 1
⇒ cos 2 (x/2) = – √15/8 + 1/2
cos(x/2) = ± (4-√15)/8
Se da que x está en el segundo cuadrante, por lo que cos(x/2) es positivo.
cos(x/2) = (4 – √15)/8
Otra vez,
cosx = cos 2 (x/2) – sen 2 (x/2)
⇒ – √15/4 = {(4 – √15)/8} 2 – sen 2 (x/2)
⇒ sen 2 (x/2) = (4 + √15)/8
⇒ sin(x/2) = ± √{(4 + √15)/8} = √{(4 + √15)/8}
Ahora,
tan(x/2) = sin(x/2) / cos(x/2)
=
=
=
=
=
= 4 + √15
Por lo tanto, el valor de cos(x/2) = (4 – √15)/8, sin(x/2) = √{(4 + √15)/8}, y tan(x/2) = 4 + √15 .
Pregunta 30(ii). Si cosx = 4/5 yx es aguda, encuentre tan2x.
Solución:
Dado que,
cos x = 4/5
Como sabemos, senx = √(1 – cos 2 x)
Asi que,
= √(1 – (4/5) 2 )
= √(1 – 16/25)
= √{(25 – 16)/25}
= √(9/25)
= 3/5
Como tanx = senx/cosx, entonces
= (3/5) / (4/5)
= 3/4
Como sabemos que,
tan2x = 2tanx / (1 – tan 2x )
= 2(3/4) / {1 – (3/4) 2 }
= 2(3/4) / (1 – 9/16)
= (3/2) / (7/16)
= 24/7
Por lo tanto, el valor de tan2x es 24/7
Pregunta 30(iii). Si senx = 4/5 y 0 < x < π/2, encuentre el valor de sen4x.
Solución:
Dado que,
senx = 4/5
Como sabemos, senx = √(1 – cos 2 x)
Asi que,
⇒ (4/5) 2 = 1 – porque 2 x
⇒ 16/25 – 1 = -cos 2 x
⇒ 9/25 = cos 2 x
⇒cosx = ±3/5
Se da que, x está en el 1er cuadrante
Entonces, cos x = 3/5
Ahora,
sen4x = 2 sen2x cos2x
= 2 (2 senx cosx)(1 – 2sen 2 x)
= 2(2 × 4/5 × 3/5)(1 – 2(4/5) 2 )
= 2(24/25)(1-32/25)
= 2(24/25)((25-32)/25)
= 2(24/25)(-7/25)
= -336/625
Por lo tanto, el valor de sen4x es (- 336/625)
Pregunta 31. Si tanx = b/a, encuentra el valor de 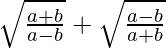
Solución:
Tenemos que encontrar el valor de
Asi que,
=
Se da que tanx = b/a, entonces
=
=
=
=
=
=
Por lo tanto, el valor de
es
Pregunta 32. Si tanA = 1/7 y tanB = 1/3, demuestre que cos2A = sen4B
Solución:
Dado que, tanA = 1/7 y tanB = 1/3
Mostrar: cos2A = sen4B
Como sabemos, tan2B = 2tanB / (1 – tan 2 B)
= (2 × 1/3)(1 – 1/9) = 3/4
Entonces, cos2A = (1 – tan 2 A)/(1 + tan 2 A)
= {1-(1/7) 2 }/{1+(1/7) 2 }
= 48/50
= 24/25
Y sen4B = 2tan2B / (1 + tan 2 2B)
= {2 × 3/4}{1 + (3/4) 2 }
= 24/25
Por lo tanto, cos2A = sen4B
Pregunta 33. cos7° cos14° cos28° cos56° = sen68°/16cos83°
Solución:
Resolvamos LHS
= cos7° cos14° cos28° cos56°
Al dividir y multiplicar por 2sen7°, obtenemos
=
× 2sen7° × cos7° × cos14° × cos28° × cos56°
=
× cos28° × cos56°
=
× cos56°
=
=
=
LHS = RHS
Por lo tanto probado.
Pregunta 34. Probó que, cos(2π/15)cos(4π/15)cos(8π/15)cos(16π/15) = 1/16
Solución:
Resolvamos LHS
= cos(2π/15)cos(4π/15)cos(8π/15)cos(16π/15)
Al dividir y multiplicar por 2sin(2π/15), obtenemos
=
=
=
=
=
=
= 1/16
LHS = RHS
Por lo tanto probado.
Pregunta 35. Probó que, cos(π/5)cos(2π/5)cos(4π/5)cos(8π/5) = -1/16
Solución:
Resolvamos LHS
= cos(π/5)cos(2π/5)cos(4π/5)cos(8π/5)
Al dividir y multiplicar por 2sin(2π/5), obtenemos
=
× 2sen(π/5)cos(π/5)cos(2π/5)cos(4π/5)cos(8π/5)
=
(sen(2π/5)cos(2π/5)cos(4π/5)cos(8π/5))
=
[2sen(2π/5)cos(2π/5)cos(4π/5)cos(8π/5)]
=
[sen(4π/5)cos(4π/5)cos(8π/5)]
=
[2sen(4π/5)cos(4π/5)cos(8π/5)]
=
[sen(8π/5)cos(8π/5)]
=
[2sen(8π/5)cos(8π/5)]
=
=
=
= -1/16
LHS = RHS
Por lo tanto probado.
Pregunta 36. Probó que, cos(π/65)cos(2π/65)cos(4π/65)cos(8π/65)cos(16π/65)cos(32π/65) = 1/64
Solución:
Resolvamos LHS
= cos(π/65)cos(2π/65)cos(4π/65)cos(8π/65)cos(16π/65)cos(32π/65)
Ahora al dividir y multiplicar por 2sin(π/65), obtenemos
=
× 2sen(π/65)cos(π/65)cos(2π/65)cos(4π/65)cos(8π/65)cos(16π/65)cos(32π/65)
=
× [cos(2π/65) × cos(4π/65) × cos(8π/65) × cos(16π/65) × cos(32π/65)]
=
× coseno(4π/65) × coseno(8π/65) × coseno(16π/65) × coseno(32π/65)
=
× cos(8π/65) × cos(16π/65) × cos(32π/65)
=
× cos(16π/65) × cos(32π/65)
=
× cos(32π/65)
=
=
=
= 1/64
LHS = RHS
Por lo tanto probado
Pregunta 37. Si 2tanα = 3tanβ, prueba que tan(α – β) = sen2β / (5 – cos2β)
Solución:
Dado que,
2tanα = 3tanβ
Demostrar: tan(α – β) = sen2β / (5 – cos2β)
Prueba:
Resolvamos LHS
=
=
=
=
=
=
=
=
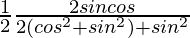
=
=
=
=
=
=
LHS = RHS
Por lo tanto probado.
Pregunta 38(i). Si senα + senβ = a y cosα + cosβ = b, demuestre que sen(α + β) = 2ab/(a 2 + b 2 )
Solución:
Dado que,
sinα + sinβ = a y cosα + cosβ = b
Demostrar: sen(α + β) = 2ab/(a 2 + b 2 )
Prueba:
Como sabemos que,
entonces
……(yo)
Ahora, usando la identidad
…..(ii)
Ahora al dividir la ecuación (i) y (ii), obtenemos
tan(α + β)/2 = a/b
Como sabemos que,
sen2x = 2 tanx/(1 + tan 2 x)
=
= 2ab/(a 2 + b 2 )
LHS = RHS
Por lo tanto probado
Pregunta 38(ii). Si senα + senβ = a y cosα + cosβ = b, demuestre que cos(α – β) = (a 2 + b 2 – 2)/2
Solución:
Dado que,
senα + senβ = a ……(i)
cosα + cosβ = b …….(ii)
Ahora, al elevar al cuadrado las ecuaciones (i) y (ii) y luego sumarlas, obtenemos
sen 2 α + sen 2 β + 2sinαsinβ + cos 2 α + cos 2 β + 2cosαcosβ = a 2 + b 2
⇒ 1 + 1 + 2(sinαsinβ + cosαcosβ) = a 2 + b 2
⇒ 2(sinαsinβ + cosαcosβ) = a 2 + b 2 – 2
⇒ 2 cos(α – β) = a 2 + b 2 – 2
⇒ cos(α – β) = (a 2 + b 2 – 2)/2
Por lo tanto probado.
Pregunta 39. Si 2tan(α/2) = tan(β/2), prueba que cosα = 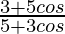
Solución:
Dado que,
2tan(α/2) = tan(β/2)
Demostrar: cosα =
Prueba:
Resolvamos RHS
=
=
=
=
=
=
=
= cosα
RHS = LHS
Por lo tanto probado.
Pregunta 40. Si cosx = 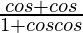 , demuestre que tan(x/2) = ± tan(α/2)tan(β/2).
, demuestre que tan(x/2) = ± tan(α/2)tan(β/2).
Solución:
Dado que,
…..(i)
⇒
Ahora, por componendo y dividendo, obtenemos
⇒
⇒
⇒
⇒
⇒ bronceado 2 (x/2) = bronceado 2 (α/2) bronceado 2 (β/2)
⇒ tan(x/2) = ±tan(α/2)tan(β/2)
Por lo tanto Probado.
Pregunta 41. Si sec(x + α) + sec(x – α) = 2secx, prueba que cosx = ± √2 cos(α/2).
Solución:
Dado que,
segundo(x + α) + segundo(x – α) = 2segx
Asi que,
⇒
⇒
⇒
⇒ cos 2 xcosα = cos 2 x(cos 2 α + sen 2 α) – sen 2 α
⇒ cos 2 x(1 – cosα) = sen 2 α
⇒
=
⇒ cosx = ± √2 cos(α/2)
Por lo tanto probado
Pregunta 42. Si cosα + cosβ = 1/3 y senα + sinβ = 1/4, demuestre que cos(α – β)/2 = ±5/24.
Solución:
Dado que,
cosα + cosβ = 1/3
sinα + sinβ = 1/4, obtenemos
Demostrar: cos(α – β)/2 = ±5/24
Prueba:
(cos 2 α + cos 2 β + cosαcosβ) + (sen 2 α + sen 2 β + 2sinαsenβ) = 1/9 + 1/16
1 + 1 + 2(cosαcosβ + sinαsinβ) = 25/144
2 + 2cos(α – β) = -263/288 …..(i)
Ahora,
=
[De (i)]
= 25/576
= ± 5/24
Por lo tanto probado.
Pregunta 43. Si senα = 4/5 y cosβ = 5/13, prueba que cos{(α – β)/2} = 8/√65.
Solución:
Dado que,
senα = 4/5 y cosβ = 5/13
Como sabemos eso.
cosα = √(1 – sen 2 α)
Asi que,
= √{1 – (4/5) 2 }
= 3/5
Además, senβ = √(1 – cos 2 β)
= √{1 – (5/13) 2 }
= 12/13
Ahora,
cos(α – β) = cosα cosβ + sinα sinβ
= (3/5)(5/13)(4/5)(12/13)
= 63/65
De este modo,
cos{(α – β)/2} =
=
= 8/√65
Por lo tanto Probado.
Pregunta 44. Si acos2θ + bsin2θ = c tiene como raíces α y β prueba que,
(i) tanα + tanβ = 2b/(a + c)
(ii) tanα tanβ = (c – a)/(c + a)
(iii) tan(α + β) = b/a
Solución:
Como sabemos que
Ahora sustituimos estos valores en la ecuación dada, obtenemos
a(1 – tan 2 θ) + b(2tan θ) = c(1 + tan 2 θ)
(c + a)tan 2 θ + 2btanθ + c – a = 0
(i) Como α y β son raíces
Entonces, suma de las raíces:
tanα + tanβ = 2b / (c + a)
(ii) Como α y β son raíces
Entonces, producto de raíces:
tanα tanβ = (c – a) / (c + a)
(iii) tan(α + β)=
=
= b/a
Por lo tanto probado.
Pregunta 45. Si cosα + cosβ = 0 = sinα + sinβ, entonces prueba que cos2α + cos2β = -2cos(α + β).
Solución:
Dado que,
cosα + cosβ = 0 = senα + senβ
Demostrar: cos2α + cos2β = -2cos(α + β)
Prueba:
cosα + cosβ = 0
Al elevar al cuadrado en ambos lados, obtenemos
cos 2 α + cos 2 β + 2 cosα cosβ = 0 ….(i)
Similarmente
sinα + sinβ = 0
Al elevar al cuadrado en ambos lados, obtenemos
sen 2 α + sen 2 β + 2 senα senβ = 0 …..(ii)
Ahora, restando la ecuación (ii) de (i), obtenemos
⇒ (cos 2 α + cos 2 β + 2 cosα cosβ) – (sen 2 α + sen 2 β + 2 senα senβ) = 0
⇒ cos 2 α – sen 2 α + cos 2 β – sen 2 β + 2(cosα cosβ – senα senβ) = 0
⇒ cos2α + cos2β + 2cos(α + β) = 0
⇒ cos2α + cos2β = -2cos(α + β)
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
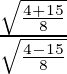
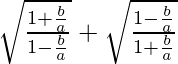
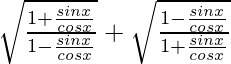
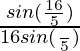
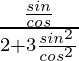
![Rendered by QuickLaTeX.com sin(α+β)=\frac{2tan[\frac{(α+β)}{2}]}{1+tan^2[\frac{(α+β)}{2}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-084e9356b7903d17c0e812fcb05679b6_l3.png)