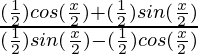Acreditar las siguientes identidades:
Pregunta 1. √[(1 – cos2x)/(1 + cos2x)] = tanx
Solución:
Resolvamos LHS,
= √[(1 – cos2x)/(1 + cos2x)]
Como sabemos que, cos2x =1 – 2 sen 2 x
= 2 cos 2 x – 1
Asi que,
= √[(1 – cos2x)/(1 + cos2x)]
= √[(1 – (1 – 2sen 2 x))/(1 + (2cos 2 x – 1))]
= √(1 – 1 + 2sen 2 x)/(1 + 2cos 2 x – 1)1
= √[2 sen 2 x/2 cos 2 x]
= senx / cosx
= tangente
LHS = RHS
Por lo tanto probado.
Pregunta 2. sen2x/(1 – cos2x) = cotx
Solución:
Resolvamos LHS,
= sen 2x/(1 – cos 2x)
Como sabemos que,
cos 2x = 1 – 2 sen 2 x
sen 2x = 2 sen x cos x
Asi que,
sen 2x/(1-cos 2x) = (2 sen x cos x)/(1 – (1 – 2sen 2 x))
= (2 sen x cos x)/(1 – 1 + 2 sen 2 x)]
= [2 sen x cos x/2 sen 2 x]
= cos x/sen x
= cuna x
LHS = RHS
Por lo tanto probado.
Pregunta 3. sen 2x/(1 + cos 2x) = tan x
Solución:
Resolvamos LHS,
= sen 2x / (1+cos 2x)
Como sabemos que,
cos 2x = 1 – 2 sen 2 x
= 2 cos 2 x – 1
sen 2x = 2 sen x cos x
Asi que,
sen 2x / (1 + cos2x) = [2 sen x cos x / (1 + (2cos 2 x – 1))]
= [2 sen x cos x / (1+2 cos 2 x – 1)]
= [2 sen x cos x/2 cos 2 x]
= sen x/cos x
= bronceado x
LHS = RHS
Por lo tanto probado.
Pregunta 4. 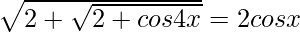 , 0 < r < π/4
, 0 < r < π/4
Solución:
Resolvamos LHS,
Como sabemos que,
cos 2x = 2 cos 2 x – 1 ⇒ cos 4x = 2 cos 2 2x – 1
Asi que,
=
=
=
=
=
=
= 2 cos x
LHS = RHS
Por lo tanto probado.
Pregunta 5. [1 – cos 2x + sen 2x]/[1 + cos 2x + sen 2x] = tan x
Solución:
Resolvamos LHS,
= [1 – cos 2x + sen 2x]/[1 + cos 2x + sen 2x]
Como sabemos que,
cos 2x = 1 – 2 sen 2 x
= 2 cos 2 x – 1
sen 2x = 2 sen x cos x
Asi que,
= {1 – (1 – 2sen 2 x) + 2senxcosx} / {1 + (2 cos 2 x – 1) + 2 sen x cosx}
= {1 − 1 + 2sen 2 x + 2senxcosx} / {1 + 2cos 2 x − 1 + 2senx cosx}
= {2 sen 2 x + 2 senxcosx} / {2 cos 2 x + 2 senxcosx}
= {2senx (senx + cosx)} / {2 cos x (cosx + sen x)}
= senx/cosx
= bronceado x
LHS = RHS
Por lo tanto probado.
Pregunta 6. [sen x + sen 2x]/[1 + cos x + cos2x] = tanx
Solución:
Resolvamos LHS,
= [sen x + sen 2x]/[1 + cos x + cos 2x]
Como sabemos que,
cos 2x = cos 2 x sen 2 x
sen 2x = 2 sen x cos x
Asi que,
{sen x + sen 2x} / {1 + cos x + cos 2x} = {sen x + 2 sen x cos x} / {1 + cosx + ( 2 cos 2 x − 1)}
= {senx + 2 senx cos x} / {1 + cosx + 2cos 2 x − 1}
= {sen x + 2 sen x cosx} / {cosx + 2cos 2 x}
= {senx (1 + 2 cos x)} / {cosx (1 + 2cosx)}
= senx / cosx
= bronceado x
LHS = RHS
Por lo tanto probado.
Pregunta 7. cos 2x / (1+ sen 2x) = tan (π/4 – x)
Solución:
Resolvamos LHS,
= cos 2x / (1 + sen 2x)
Como sabemos que,
cos 2x = cos 2 x – sen 2 x
sen 2x = 2 sen x cos x
Asi que,
{cos 2x} / {1 + sen 2x} = {cos 2 x – sen 2 x} / {1 + 2 sen x cos x}
= {(cosx – senx)(cosx + senx)} / {sen 2 x + cos 2 x + 2 sen x cos x}
Ya que, a 2 – b 2 = (a – b)(a + b) y sen 2 x + cos 2 x = 1
Asi que,
= {(cosx – senx)(cosx + senx)} / {(senx + cos x) 2
Ya que, a 2 + b 2 + 2ab = (a + b) 2
Asi que,
= {(cosx – senx)(cosx + senx)} / {(senx + cosx)(senx + cosx)}
= (cos x – sen x) / (sen x + cos x)
Ahora, multiplicando el numerador y el denominador por 1/√2, obtenemos,
=
=
=
Como, 1/√2 = sen π/4, entonces
=
Usando las fórmulas, obtenemos
sen(A – B) = senA cosB – senB cosA
cos(A – B)= cosA cosB + senA senB
= bronceado (π/4 – x)
LHS = RHS
Por lo tanto probado.
Pregunta 8. cos x/(1 – sen x) = tan (π/4 + x/2)
Solución:
Resolvamos LHS,
= cos x/(1 – sen x)
Como sabemos que,
cos 2x = cos 2 x – sen 2 x
cos x = cos 2 x/2 – sen 2 x/2
sen 2x = 2 sen x cos x
sen x = 2 sen x/2 cos x/2
Asi que,
=
Usando las fórmulas,
a 2 – b 2 = (a – b)(a + b) y sen 2 x + cos 2 x = 1), obtenemos
=
=
=
=
Ahora multiplicamos numerador y denominador por 1/√2, obtenemos,
=
=
=
=
= bronceado (π/4 – x)
LHS = RHS
Por lo tanto probado.
Pregunta 9. cos 2 π/8 + cos 2 3π/8 + cos 2 5π/8 + cos 2 7π/8 = 2
Solución:
Resolvamos LHS,
= cos 2 π/8 + cos 2 3π/8 + cos 2 5π/8 + cos 2 7π/8
Como sabemos que,
cos 2x = 2 cos 2 x – 1
cos 2x+1=2 cos 2 x
cos 2 x = (cos 2x + 1)/2
Asi que,
= cos 2 π/8 + cos 2 3π/8 + cos 2 5π/8 + cos 2 7π/8
=
=
=
Como sabemos que, cos (π – A) =- cos A, cos (π+ A) = -cos A y cos (2π – A) = cos A
= 2 x {1 + cos(2π/8)/2} + 2 x {1 – cos(2π/8)/2}
= 1 + cos(2π/8) + 1 – cos(2π/8)
= 2
LHS = RHS
Por lo tanto Probado.
Pregunta 10. sen 2 π/8 + sen 2 3π/8 + sen 2 5π/8 + sen 2 7π/8
Solución:
Resolvamos LHS,
= sen 2 π/8 + sen 2 3π/8 + sen 2 5π/8 + sen 2 7π/8
Como sabemos que,
cos 2x = 1 – 2sen 2 x
2sen 2x = 1 – cos 2x
sen 2 x = (1 – cos 2x)/2
Asi que,
=
=
=
Como sabemos, cos (π – A) = -cos A, cos (π + A) = -cos A y cos (2π – A) = cos A
= 2 x {1 – cos(2π/8)/2} + 2 x {1 + cos(2π/8)/2}
= 1 – coseno(2π/8) + 1 + coseno(2π/8)
= 2
LHS = RHS
Por lo tanto probado.
Pregunta 11. (cos α + cos β) 2 + (sen α + sen β) 2 = 4 cos 2 (α – β)/2
Solución:
Resolvamos LHS,
= (cos α+ cos β) 2 + (sen α+ sen β) 2
Al expandir, obtenemos,
= cos 2 α + cos 2 β + 2 cos α cos β + sen 2 α+ sen 2 β + 2 sen α sen β
= 2+2 cos α cos β + 2 sen α sen β
= 2 (1+ cos α cos β+ sen α sen β)
= 2 (1 + cos (α – β)) [Usando, cos (A – B) = cos A cos B+ sen A sen B]
= 2 (1 + 2 cos 2 (α – β)/2 – 1) [Usando, cos2x = 2 cos 2 x – 1]
= 2 (2 cos 2 (α – β)/2)
= 4 cos 2 (α – β)/2
LHS = RHS
Por lo tanto Probado.
Pregunta 12. sen 2 (π/8 + x/2) – sen 2 (π/8 – x/2) = 1/√2 sen x
Solución:
Resolvamos LHS,
= sen 2 (π/8 + x/2) – sen 2 (π/8 – x/2)
Como sabemos que,
sen 2 A – sen 2 B = sen (A + B) sen (AB)
Asi que,
sen 2 (π/8 + x/2) – sen 2 (π/8 – x/2) = sen (π/8 + x/2 + π/8 – x/2) sen (π/8 + x/ 2 – (π/8 – x/2))
= sen (π/8 + π/8) sen (π/8 + x/2 – π/8 + x/2)
= sen π/4 sen x
= 1/√2 sen x [Como sabemos, π/4 = 1/√2]
LHS = RHS
Por lo tanto probado.
Pregunta 13. 1 + cos 2 2x = 2 (cos 4 x + sen 4 x)
Solución:
Resolvamos LHS,
= 1 + cos 2 2x
Como sabemos que,
cos2x = cos 2 x sen 2 x
cos 2 x+ sen 2 x = 1
Asi que,
1 + cos 2 2x = (cos 2 x+ sen 2 x) 2 + (cos 2 x – sen 2 x) 2
= (cos 4 x + sen 4 x + 2 cos 2 x sen 2 x) + (cos 4 x + sen 4 x – 2 cos 2 x sen 2 x)
= cos 4 x + sen 4 x + cos 4 x + sen 4 x
= 2 cos 4 x + 2 sen 4 x
= 2 (cos 4 x + sen 4 x)
LHS = RHS
Por lo tanto probado.
Pregunta 14. cos 3 2x + 3 cos 2x = 4 (cos 6 x – sen 6 x)
Solución:
Resolvamos RHS,
= 4 (cos 6 x – sen 6 x)
Al expandir, obtenemos,
4 (cos 6 x – sen 6 x) = 4 [(cos 2 x) 3 – (sen 2 x) 3 ]
= 4 (cos 2 x – sen 2 x) (cos 4 x + sen 4 x + cos 2 x sen 2 x)
Ahora, usando la fórmula, obtenemos
a 3 – b 3 = (a – b) (a 2 + b 2 + ab)
= 4 cos 2x (cos 4 x + sen 4 x + cos 2 x sen 2 x + cos 2 x sen 2 x – cos 2 x sen 2 x
Como sabemos que,
cos 2x = cos 2 x – sen 2 x
Asi que,
= 4 cos 2x (cos 4 x + sen 4 x + 2 cos 2 x sen 2 x – cos 2 x sen 2 x)
= 4 cos 2x [(cos 2 x) 2 + (sen 2 x) 2 + 2 cos 2 x sen 2 x – cos 2 x sen 2 x]
Usando la fórmula,
a 2 + b 2 + 2ab = (a + b) 2 , obtenemos
= 4 cos 2x [(1) 2 – 1/4 (4 cos 2 x sen 2 x)]
= 4 cos 2x [(1) 2 -1/4 (2 cos x sen x) 2 ]
Ya que
sen 2x = 2 sen x cos x
= 4 cos 2x [(1 2 ) – 1/4 (sen 2x) 2 ]
= 4 cos 2x (1 – 1/4 sen 2 2x)
Ya que
sen 2 x = 1 – cos 2 x
= 4 cos 2x [1 – 1/4 (1 – cos 2 2x)]
= 4 cos 2x [1 – 1/4 + 1/4 cos 2 2x]
= 4 cos 2x [3/4 + 1/4 cos 2 2x]
= 4 (3/4 cos 2x + 1/4 cos³ 2x)
= 3 cos 2x + cos 3 2x
= cos 3 2x + 3 cos 2x
LHS = RHS
Por lo tanto probado.
Pregunta 15. (sen 3A + sen A) sen A + (cos 3A – cos A) cos A = 0
Solución:
Resolvamos LHS,
= (sen 3A + sen A) sen A + (cos 3A – cos A) cos A
= (sen 3A) (sen A) + sen 2 A + (cos 3A) (cos A) – cos 2 A
= [(sen 3A) (sen A) + (cos 3A) (cos A)] + (sen 2 A – cos 2 A)
= [(sen 3A) (sen A) + (cos 3A) (cos A)] – (cos 2 A – sen 2 A)
= coseno (3A – A) – coseno 2A
Como sabemos que,
cos 2x = cos 2 A – sen 2 A
cos A cos B + sen A sen B = cos (A – B)
Asi que,
= cos 2A – cos 2A
= 0
LHS = RHS
Por lo tanto Probado.
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
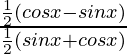
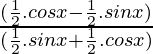
![Rendered by QuickLaTeX.com \frac{\frac{1}{√2}[cos(\frac{x}{2})+sin(\frac{x}{2})]}{\frac{1}{√2}[sin(\frac{x}{2})-cos(\frac{x}{2})]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d4a0ad0e2bba8c67e1e0547194680501_l3.png)