Clase 11 Soluciones RD Sharma – Capítulo 20 Progresiones geométricas – Ejercicio 20.3

Pregunta 12. Encuentra la suma: 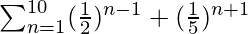$\sum_{n=1}^{10}(\frac{1}{2})^{n-1}+(\frac{1}{5})^{n+1}$

Solución:

La suma dada se puede escribir como,

S = $\sum_{n=1}^{10}(\frac{1}{2})^{n-1}+\sum_{n=1}^{10}(\frac{1}{5})^{n+1}$

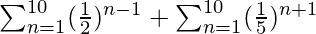
= (1 + 1/2 + 1/2 ² + . . . . 10 términos) + (1/5 ² + 1/5 ³ + 1/5 ⁴ + . . . . 10 términos)

= $\left[\frac{1-\frac{1}{2^{10}}}{1-\frac{1}{2}}\right]+\left[\frac{1-\frac{1}{5^{10}}}{1-\frac{1}{5}}\right]$

= $\frac{2^{10}-1}{2^9}+\frac{5^{10}-1}{4(5^{11})}$

Por lo tanto, la suma de la serie es $\frac{2^{10}-1}{2^9}+\frac{5^{10}-1}{4(5^{11})}$ .

Pregunta 13. El quinto término de un GP es 81 mientras que su segundo término es 24. Encuentra la serie y la suma de sus primeros ocho términos.

Solución:

Sabemos que el término n de GP viene dado por, a _n = ar ^n-1 .

De acuerdo con la pregunta, tenemos,

=> ar ⁴ = 81 . . . . (1)

=> ar = 24 . . . . (2)

Dividiendo (2) por (1),

=> ^r3 = 81/24

=> ^r3 = 27/8

=> r = 3/2

Poniendo r = 3/2 en (2), obtenemos,

=> un = (24)(2)/3

=> un = 16

Sabemos que la suma de n términos de GP viene dada por, S _n = a(r ⁿ −1)/(r−1).

Entonces, S ₈ = 16[(3/2) ⁸ −1]/[(3/2)−1]

= 16[3 ⁸ − 2 ⁸ ]/2 ⁷

= 6305/8

Como a = 16 y r = 3/2, la serie sería 16, 24, 36, 54, . . . .

Además, la suma de los primeros 8 términos de GP es 6305/8.

Pregunta 14. Si S ₁ , S ₂ , S ₃ son respectivamente la suma de n, 2n, 3n términos de un GP, entonces demuestre que S ²₁ +S ²₂ = S ₁ (S ₂ +S ₃ ).

Solución:

Se nos da,

S ₁ = Suma de n términos = a[1−r ⁿ ]/(1−r)

S ₂ = Suma de 2n términos = a[1−r ²ⁿ ]/(1−r)

S ₃ = Suma de 3n términos = a[1−r ³ⁿ ]/(1−r)

Tenemos,

IZQ = S ²₁ +S ²₂

= $\left[\frac{a(1-r^n)}{1-r}\right]^2+\left[\frac{a(1-r^{2n})}{1-r}\right]^2$

= $\frac{a^2}{(1-r)^2}[(1-r^n)^2+(1-r^{2n})^2]$

= $\frac{a^2}{(1-r)^2}[1+r^{2n}-2r^n+1+r^{4n}-2r^{2n}]$

= $\frac{a^2}{(1-r)^2}[2-r^{2n}-2r^n+r^{4n}]$

Y RHS = S ₁ (S ₂ + S ₃ )

= $\frac{a(1-r^n)}{1-r}\left[\frac{a(1-r^{2n})}{1-r}+\frac{a(1-r^{3n})}{1-r}\right]$

= $\frac{a^2}{(1-r)^2}[(1-r^n)(1-r^{2n})+(1-r^n)(1-r^{3n})]$

= $\frac{a^2}{(1-r)^2}[1-r^{2n}-r^n+r^{3n}+1-r^{3n}-r^n+r^{4n}]$

= $\frac{a^2}{(1-r)^2}[2-r^{2n}-2r^n+r^{4n}]$

= LHS

Por lo tanto, probado.

Pregunta 15. Muestre que la razón de la suma de n términos de un GP a la suma de términos de (n+1) ^th a (2n) ^th término es 1/r ⁿ .

Solución:

Sabemos que la suma de n términos de un GP está dada por, S ₁ = a[1−r ⁿ ]/(1−r).

Y la suma de los términos de (n+1) ^th a (2n) ^th término será,

S ₂ = ar ^norte + ar ^norte+1 + ar ^norte+2 + . . . . ar ^2n-1

= ar norte [1−r ^norte^] /(1−r)

IZQ = $\frac{S_1}{S_2} = \frac{\frac{a(1-r^n)}{1-r}}{\frac{ar^n(1-r^n)}{1-r}}$

= 1/r ^norte

= lado derecho

Por lo tanto, probado.

Pregunta 16. Si a y b son raíces de x ² – 3x + p = 0 y c, d son raíces de x ² – 12x + q = 0, donde a, b, c, d, forman un GP Demuestra que ( q + p):(q – p) = 17:15.

Solución:

Se nos da que a, b, c, d están en GP. Supongamos que la razón común es r.

Entonces, b=ar, c=ar ² y d=ar ³

Ahora a y b son las raíces de x ² – 3x + p = 0.

Suma de raíces = a + b = 3

=> a + ar = 3

=> a(1+r) = 3 ….. (1)

Producto de raíces = ab = p

=> a(ar) = p

=> un ² r = p ….. (2)

Y c, d son las raíces de x ² − 12x + q = 0

Suma de raíces = c + d = 12

=> ar ² + ar ³ = 12

=> ar ² (1+r) = 12 ….. (3)

Producto de raíces = cd = q

=> ar ² (ar ³ ) = q

=> a ² r ⁵ = q ….. (4)

Dividiendo la ecuación (3) por (1), obtenemos,

=> $\frac{ar^2(1+r)}{a(1+r)}$ = $\frac{12}{3}$

=> r ² = 4

=> r = ±2

Cuando r=2, de (1), obtenemos,

=> un(1+2) = 3

=> un = 1

Poniendo a=1 y r=2 en (2),

=> p = (1) ² (2) = 2

De (4) obtenemos,

q = (1) ² (2) ⁵ = 32

Ahora LHS = $\frac{q+p}{q−p}$ = $\frac{32+2}{32−2}$ = $\frac{34}{30}$ = $\frac{17}{15}$

= lado derecho

Cuando r=−2, de (1), obtenemos,

=> a(1−2) = 3

=> un = −3

Poniendo a=−3 y r=−2 en (2),

p = (−3) ² (−2) = −18

De (4) obtenemos,

q = (−3) ² (−2) ⁵ = −288

Ahora LHS = $\frac{q+p}{q−p}$ = $\frac{−288+(−18)}{−288−(−18)}$ = $\frac{−306}{−270}$ = $\frac{17}{15}$

= lado derecho

Por lo tanto, probado.

Pregunta 17. ¿Cuántos términos del GP 3, 3/2, 3/4,… se necesitan para dar la suma 3069/512?

Solución:

Dado que GP tiene el primer término (a) = 3, razón común (r) = (3/2)/3 = 1/2 y suma de términos (S _n ) = 3069/512.

Sabemos que la suma de n términos de un GP está dada por S _n = a(r ⁿ –1)/(r–1).

=> 3069/512 = 3[1–(1/2) ⁿ ] / [1–(1/2)]

=> 2(2 ⁿ –1)/(2 ⁿ ) = 1023/512

=> 1023(2) ⁿ = 1024(2) ⁿ – 1024

=> 2 ⁿ = 1024

=> norte = 10

Por lo tanto, 10 términos del GP deben tomarse juntos para hacer 3069/512.

Pregunta 18. Una persona tiene 2 padres, 4 abuelos, 8 bisabuelos , etc. Encuentre el número de sus antepasados durante las diez generaciones anteriores a la suya.

Solución:

Tenemos la secuencia, 2,4,8, . . . . que forma un GP con primer término (a) = 2 y razón común (r) = 4/2 = 2.

Sabemos que la suma de n términos de un GP está dada por S _n = a(r ⁿ –1)/(r–1).

Número de antepasados durante las diez generaciones = Suma de los primeros 10 términos del PG

S ₁₀ = 2(2 ¹⁰ –1)/(2–1)

= 2(1023)

= 2046

Por lo tanto, el número de sus antepasados durante las diez generaciones anteriores a la suya es 2046.

Pregunta 19. S ₁ , S ₂ , S ₃ , . . . ., S _n son las sumas de n términos de GP’s cuyo primer término es 1 en cada uno y las razones comunes son 1,2,3, . . . ., n respectivamente, luego demuestre que S ₁ + S ₂ + 2S ₃ + 3S ₄ + . . . . _{+ ( n} –1)S norte = 1 ^norte + 2 ^norte + 3 ^norte + . . . . + norte ^norte

Solución:

S ₁ , S ₂ , S ₃ , . . . ., S _n son las sumas de n términos de GP’s cuyo primer término es 1 en cada uno y las razones comunes son 1,2,3, . . . ., n respectivamente.

Aquí para S ₁ , la serie será 1,1,1,1, . . . hasta n términos como primer término (a) y razón común (r) ambos son iguales a 1.

Entonces, S ₁ = 1+1+1+1+ . . . . hasta n términos = n

Entonces, LHS = S ₁ + S ₂ + 2S ₃ + 3S ₄ + . . . . + (n–1) _Sn

= $n+\frac{2^n-1}{2-1}+2(\frac{3^n-1}{3-1})+3(\frac{4^n-1}{4-1})+....+(n-1)(\frac{n^n-1}{n-1})$

= norte + (2 ^norte – 1) + (3 ^norte – 1) + (4 ^norte – 1) + . . . . (n ^norte – 1)

= n + (2 ⁿ + 3 ⁿ + 4 ⁿ +. . . . + n ⁿ ) – (1 + 1 +1 + 1 + . . . . (n–1) términos)

= norte + (2 ^norte + 3 ^norte + 4 ^norte +. . . . + norte ^norte ) – norte + 1

= 1 + 2 ^norte + 3 ^norte + 4 ^norte +. . . . + norte ^norte

= 1 ^norte + 2 ^norte + 3 ^norte + 4 ^norte +. . . . + norte ^norte

= lado derecho

Por lo tanto, probado.

Pregunta 20. Un GP consta de un número par de términos. Si la suma de todos los términos es 5 veces la suma de los términos que ocupan los lugares impares. Encuentre la razón común del GP

Solución:

Como el número de términos es par, sea 2n el número de términos del GP.

Según la pregunta,

Suma de todos los términos = 5 (Suma de los términos que ocupan los lugares impares)

=> un ₁ + un ₂ + un ₃ + . . . . + un _n = 5 (un ₁ + un ₃ + un ₅ + . . . . un _2n–1 )

=> un + ar + ar ² + . . . . + ar ^n–1 = 5 (a + ar ² + ar ⁴ + . . . . + ar ^2n–2 )

=> a(1–r ²ⁿ )/(1–r) = 5a(1–r ²ⁿ )/(1–r ² )

=> a/(1–r) = 5a/(1–r ² )

=> a/(1–r) = 5a/[(1–r)(1+r)]

=> 5/(1+r) = 1

=> 1+r = 5

=> r = 4

Por lo tanto, la razón común del GP es 4.

Pregunta 21. Sea a _n el n-ésimo término del GP de números positivos. Sea $\sum_{n=1}^{100} a_{2n} = α$ y $\sum_{n=1}^{100} a_{2n-1} = β$ , tal que α ≠ β . Demuestre que la razón común de la GP es α/β.

Solución:

Tenemos, $\sum_{n=1}^{100} a_{2n} = α$

=> un ₂ + un ₄ + un ₆ + . . . . + un ₂₀₀ = α

=> ar + ar ³ + ar ⁵ + . . . . + ar ¹⁹⁹ = α

=> ar(r ²⁽¹⁰⁰⁾ –1)/(r–1) = α

=> ar(r ²⁰⁰ –1)/(r–1) = α . . . . (1)

También tenemos, $\sum_{n=1}^{100} a_{2n-1} = β$

=> un ₁ + un ₃ + un ₅ + . . . . + un ₁₉₉ = β

=> un + ar ² + ar ⁴ + . . . . + ar ¹⁹⁸ = β

=> a(r ²⁽¹⁰⁰⁾ –1)/(r–1) = β

=> a(r ²⁰⁰ –1)/(r–1) = β . . . . (2)

Dividiendo (2) por (1), obtenemos,

=> $\frac{\frac{ar(r^{200}-1)}{(r-1)}}{\frac{a(r^{200}-1)}{(r-1)}}$ = $\frac{α}{β}$

=> r = $\frac{α}{β}$

Por lo tanto, probado.

Pregunta 22. Encuentra la suma de 2n términos de la serie donde cada término par es ‘a’ por el término anterior y cada término impar es ‘c’ por el término anterior, siendo el primer término la unidad.

Solución:

Supongamos que tenemos la serie, a ₁ ,a ₂ ,a ₃ , . . . . un _n _

Según la pregunta, tenemos, a ₁ = 1, a ₂ = a, a ₃ = ca, a ₄ = a ² c, a ₅ = a ² c ² y así sucesivamente.

Ahora, suma de 2n términos de la serie = a ₁ + a ₂ + a ₃ + . . . . + un _2n

S _2n = 1 + un + ca + un ² do + un ² do ² + . . . . 2n términos

= (1+a) + ca(1+a) + a ² c ² (1+a) + . . . . n términos

Ahora bien, este es un GP con el primer término (a) = (1+a) y razón común (r) = ca. Entonces, obtenemos

S2n = _{_} $\frac{(1+a)[(ac)^n-1]}{ac-1}$

Por tanto, la suma de 2n términos de la serie es $\frac{(1+a)[(ac)^n-1]}{ac-1}$ .

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 20 Progresiones geométricas – Ejercicio 20.3 | conjunto 2

Pregunta 12. Encuentra la suma: $\sum_{n=1}^{10}(\frac{1}{2})^{n-1}+(\frac{1}{5})^{n+1}$

Pregunta 13. El quinto término de un GP es 81 mientras que su segundo término es 24. Encuentra la serie y la suma de sus primeros ocho términos.

Pregunta 14. Si S ₁ , S ₂ , S ₃ son respectivamente la suma de n, 2n, 3n términos de un GP, entonces demuestre que S ²₁ +S ²₂ = S ₁ (S ₂ +S ₃ ).

Pregunta 15. Muestre que la razón de la suma de n términos de un GP a la suma de términos de (n+1) ^th a (2n) ^th término es 1/r ⁿ .

Pregunta 16. Si a y b son raíces de x ² – 3x + p = 0 y c, d son raíces de x ² – 12x + q = 0, donde a, b, c, d, forman un GP Demuestra que ( q + p):(q – p) = 17:15.

Pregunta 17. ¿Cuántos términos del GP 3, 3/2, 3/4,… se necesitan para dar la suma 3069/512?

Pregunta 18. Una persona tiene 2 padres, 4 abuelos, 8 bisabuelos , etc. Encuentre el número de sus antepasados durante las diez generaciones anteriores a la suya.

Pregunta 20. Un GP consta de un número par de términos. Si la suma de todos los términos es 5 veces la suma de los términos que ocupan los lugares impares. Encuentre la razón común del GP

Pregunta 21. Sea a _n el n-ésimo término del GP de números positivos. Sea $\sum_{n=1}^{100} a_{2n} = α$ y $\sum_{n=1}^{100} a_{2n-1} = β$ , tal que α ≠ β . Demuestre que la razón común de la GP es α/β.

Pregunta 22. Encuentra la suma de 2n términos de la serie donde cada término par es ‘a’ por el término anterior y cada término impar es ‘c’ por el término anterior, siendo el primer término la unidad.

Deja una respuesta Cancelar la respuesta

Pregunta 12. Encuentra la suma:

Pregunta 13. El quinto término de un GP es 81 mientras que su segundo término es 24. Encuentra la serie y la suma de sus primeros ocho términos.

Pregunta 14. Si S 1 , S 2 , S 3 son respectivamente la suma de n, 2n, 3n términos de un GP, ​​entonces demuestre que S 2 1 +S 2 2 = S 1 (S 2 +S 3 ).

Pregunta 15. Muestre que la razón de la suma de n términos de un GP a la suma de términos de (n+1) th a (2n) th término es 1/r n .

Pregunta 16. Si a y b son raíces de x 2 – 3x + p = 0 y c, d son raíces de x 2 – 12x + q = 0, donde a, b, c, d, forman un GP Demuestra que ( q + p):(q – p) = 17:15.

Pregunta 17. ¿Cuántos términos del GP 3, 3/2, 3/4,… se necesitan para dar la suma 3069/512?

Pregunta 18. Una persona tiene 2 padres, 4 abuelos, 8 bisabuelos , etc. Encuentre el número de sus antepasados ​​durante las diez generaciones anteriores a la suya.

Pregunta 20. Un GP consta de un número par de términos. Si la suma de todos los términos es 5 veces la suma de los términos que ocupan los lugares impares. Encuentre la razón común del GP

Pregunta 21. Sea a n el n-ésimo término del GP de números positivos. Sea y , tal que α ≠ β . Demuestre que la razón común de la GP es α/β.

Pregunta 22. Encuentra la suma de 2n términos de la serie donde cada término par es ‘a’ por el término anterior y cada término impar es ‘c’ por el término anterior, siendo el primer término la unidad.

Deja una respuesta Cancelar la respuesta

Pregunta 12. Encuentra la suma: $\sum_{n=1}^{10}(\frac{1}{2})^{n-1}+(\frac{1}{5})^{n+1}$

Pregunta 14. Si S ₁ , S ₂ , S ₃ son respectivamente la suma de n, 2n, 3n términos de un GP, entonces demuestre que S ²₁ +S ²₂ = S ₁ (S ₂ +S ₃ ).

Pregunta 15. Muestre que la razón de la suma de n términos de un GP a la suma de términos de (n+1) ^th a (2n) ^th término es 1/r ⁿ .

Pregunta 16. Si a y b son raíces de x ² – 3x + p = 0 y c, d son raíces de x ² – 12x + q = 0, donde a, b, c, d, forman un GP Demuestra que ( q + p):(q – p) = 17:15.

Pregunta 18. Una persona tiene 2 padres, 4 abuelos, 8 bisabuelos , etc. Encuentre el número de sus antepasados durante las diez generaciones anteriores a la suya.

Pregunta 21. Sea a _n el n-ésimo término del GP de números positivos. Sea $\sum_{n=1}^{100} a_{2n} = α$ y $\sum_{n=1}^{100} a_{2n-1} = β$ , tal que α ≠ β . Demuestre que la razón común de la GP es α/β.