Pregunta 1. Encuentra la suma de las siguientes progresiones geométricas:
(i) 2, 6, 18, … a 7 términos
Solución:
Dado que GP tiene el primer término (a) = 2, razón común (r) = 6/2 = 3 y número de términos (n) = 7
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
S 7 = 2(3 7 –1)/(3–1)
= 2(3 7 –1)/2
= 2187–1
= 2186
Por lo tanto, la suma de 7 términos del GP es 2186.
(ii) 1, 3, 9, 27, … a 8 términos
Solución:
Dado que GP tiene el primer término (a) = 1, razón común (r) = 3 y número de términos (n) = 8
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
S 8 = 1(3 8 –1)/(3–1)
= 6560/2
= 3280
Por lo tanto, la suma de 8 términos del GP es 3280.
(iii) 1, –1/2, 1/4, –1/8, ….
Solución:
Dado que GP tiene el primer término (a) = 1, la razón común (r) = –1/2 y el número de términos (n) es infinito.
Sabemos que la suma de n términos de un GP infinito viene dada por S = a/(1–r).
S = 1/[1 – (–1/2)]
= 1/(3/2)
= 2/3
Por lo tanto, la suma de infinitos términos del GP es 2/3.
(iv) (a 2 – b 2 ), (a – b), (a–b)/(a+b), … a n términos
Solución:
Dado que GP tiene el primer término (a) = (a 2 – b 2 ), razón común (r) = (a – b)/(a 2 – b 2 ) = 1/(a+b) y el número de términos es n .
Sabemos que la suma de n términos de un GP infinito viene dada por S n = a(r n –1)/(r–1).
S norte =
=
=
Por lo tanto, la suma de n términos del GP es
.
(v) 4, 2, 1, 1/2… a 10 términos
Solución:
Dado que GP tiene el primer término (a) = 4, razón común (r) = 2/4 = 1/2 y número de términos (n) = 10.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
S 10 =
![Rendered by QuickLaTeX.com 4\left[\frac{(\frac{1}{2})^{10}-1}{(\frac{1}{2})-1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3331ec1f8cdd544042493b770bde7f53_l3.png)
=
=
=
Por lo tanto, la suma de 10 términos del GP es
.
Pregunta 2. Encuentra la suma de las siguientes series geométricas:
(i) 0.15 + 0.015 + 0.0015 + … a 8 términos
Solución:
Dado que GP tiene el primer término (a) = 0,15, razón común (r) = 0,015/0,15 = 1/10 y número de términos (n) = 8.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
S 8 =
= 0,15 (10/9) (1 – 1/10 8 )
= (1/6) (1 – 1/10 8 )
Por lo tanto, la suma de 8 términos del GP es (1/6) (1 – 1/10 8 ).
(ii) √2 + 1/√2 + 1/2√2 + …. a 8 términos
Solución:
Dado que GP tiene el primer término (a) = √2, razón común (r) = (1/√2)/√2 = 1/2 y número de términos (n) = 8.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
S 8 = √2[(1/2) 8 –1]/[(1/2)–1]
= √2(1–1/256)/(1/2)
= √2 (255/256) (2)
= (255√2)/128
Por lo tanto, la suma de 8 términos del GP es (255√2)/128.
(iii) 2/9 – 1/3 + 1/2 – 3/4 + … a 5 términos
Solución:
Dado que GP tiene el primer término (a) = 2/9, razón común (r) = (–1/3)/(2/9) = –3/2 y número de términos (n) = 5.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
S 5 =
=
=
Por lo tanto, la suma de 5 términos del GP es
.
(iv) (x + y) + (x 2 + xy + y 2 ) + (x 3 + x 2 y + xy 2 + y 3 ) + …. a n términos
Solución:
La serie dada se puede escribir como,
S norte = (x + y) + (x 2 + xy + y 2 ) + (x 3 + x 2 y + xy 2 + y 3 ) + . . . . a n términos
(x – y) S norte = (x + y) (x – y) + (x 2 + xy + y 2 ) (x – y) . . . a n términos
(x – y) S norte = x 2 – y 2 + x 3 + x 2 y + xy 2 – x 2 y – xy 2 – y 3 . . . a n términos
(x – y) S n = (x 2 + x 3 + x 4 + . . . n términos) + (y 2 + y 3 + y 4 + . . . n términos)
(x – y) S norte = x 2 [(x norte – 1)/(x – 1)] – y 2 [(y norte – 1)/(y – 1)]
S norte = [x 2 [(x norte – 1)/(x – 1)] – y 2 [(y norte – 1)/(y – 1)]]/(x – y)
Por lo tanto, la suma de n términos de la serie es [x 2 [(x n – 1)/(x – 1)] – y 2 [(y n – 1)/(y – 1)]]/(x – y) .
(v) 3/5 + 4/5 2 + 3/5 3 + 4/5 4 + … en n términos
Solución:
La serie dada se puede escribir como,
S n = (3/5 + 3/5 3 + . . . a n términos) + (4/5 2 + 4/5 4 + . . . a n términos)
=
=
=
Por lo tanto, la suma de n términos de la serie es
.
(vi) ![]()
Solución:
Dado que GP tiene el primer término (a) =
, razón común (r) =
=
y el número de términos es n.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
S norte =
=
= –ai[1–(1+i) -n ]
Por lo tanto, la suma de n términos de GP es –ai[1–(1+i) -n ].
(vii) 1, –a, a 2 , –a 3 , . . . . a n términos (a ≠ 1)
Solución:
Dado que GP tiene el primer término (a) = 1, la razón común (r) = –ay el número de términos es n.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
S norte = [(–a) norte –1]/(–a–1)
= [1–(–a) n ]/(a+1)
Por lo tanto, la suma de n términos de GP es [1–(–a) n ]/(a+1).
(viii) x 3 + x 5 + x 7 + . . . . n términos
Solución:
Dado que GP tiene el primer término (a) = x, razón común (r) = x 5 /x 3 = x 2 y el número de términos es n.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
= x 3 [x 2n –1]/[x 2 –1]
Por lo tanto, la suma de n términos de GP es x 3 [x 2n –1]/[x 2 –1].
(ix) √7 + √21 + 3√7 + . . . . n términos
Solución:
Dado que GP tiene el primer término (a) = √7, razón común (r) = √21/√7 = √3 y número de términos = n.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
S norte = √7[(√3) norte –1]/(√3–1 )
Por lo tanto, la suma de n términos de GP es √7[(√3) n –1]/(√3–1).
Pregunta 3. Evalúa lo siguiente:
(i) ![]()
Solución:
La suma dada se puede escribir como,
S 11 = (2+3 1 ) + (2+3 2 ) + (2+3 3 ) + . . . . + (2+3 11 )
= 2(11) + (3 1 + 3 2 + 3 3 + . . . . 3 11 )
= 2(11) + 3(3 11 –1)/(3–1)
= 22 + 265719
= 265741
Por lo tanto, el valor de la sumatoria es 265741.
(ii) ![]()
Solución:
La suma dada se puede escribir como,
S norte = (2+3 0 ) + (2 2 +3 1 ) + (2 3 +3 2 ) + . . . . + (2 n +3 n-1 )
= (2 1 + 2 2 + 2 3 + . . . . + 2 n ) + (3 0 + 3 1 + 3 2 + . . . . + 3 n-1 )
= 2(2 n –1)/(2–1) + 3 0 (3 n –1)/(3–1)
= 2(2 n –1) + (3 n –1)/2
Por lo tanto, el valor de la sumatoria es 2(2 n –1) + (3 n –1)/2.
(iii) ![]()
Solución:
La suma dada se puede escribir como,
S 10-2+1 = S 9 = 4 2 + 4 3 + 4 4 + . . . . 4 10
= 4 2 (4 9 –1)/(4–1)
= 16[4 9 –1]/3
Por lo tanto, el valor de la sumatoria es 16[4 9 –1]/3.
Pregunta 4. Encuentra la suma de la serie:
(i) 5 + 55 + 555 + … a n términos
Solución:
Tenemos S n = 5 + 55 + 555 + ….. hasta n términos.
Multiplicando y dividiendo por 9, obtenemos
=
[9+99+999+…a n términos]
=
[(10–1)+(10 2 –1)+(10 3 –1)…a n términos]
=
[(10+10 2 +10 3 +….n términos) – (1+1+1+…..n términos)]
=
=
Por tanto, la suma de la serie hasta n términos es
.
(ii) 7 + 77 + 777 + … a n términos
Solución:
Tenemos S n = 7 + 77 + 777 + … en n términos.
Multiplicando y dividiendo por 9, obtenemos,
=
[9+99+999+…a n términos]
=
[(10–1)+(10 2 –1)+(10 3 –1)…a n términos]
=
[(10+10 2 +10 3 +….n términos) – (1+1+1+…..n términos)]
=
=
Por tanto, la suma de la serie hasta n términos es
.
(iii) 9 + 99 + 999 + … a n términos
Solución:
Tenemos S n = 9 + 99 + 999 + … en n términos. Se puede escribir como,
= (10–1)+(10 2 –1)+(10 3 –1)…a n términos
= (10+10 2 +10 3 +….n términos) – (1+1+1+…..n términos)
=
Por tanto, la suma de la serie hasta n términos es
.
(iv) 0.5 + 0.55 + 0.555 + … a n términos
Solución:
Tenemos S n = 0.5 + 0.55 + 0.555 + … en n términos. Se puede escribir como,
=
=
=
=
=
Por tanto, la suma de la serie hasta n términos es
.
(v) 0.6 + 0.66 + 0.666 + … en n términos
Solución:
Tenemos S n = 0,6 + 0,66 + 0,666 + … en n términos. Se puede escribir como,
=
=
=
=
=
Por tanto, la suma de la serie hasta n términos es
.
Pregunta 5. ¿Cuántos términos del GP 3, 3/2, 3/4,… se toman juntos para hacer 3069/512?
Solución:
Dado que GP tiene el primer término (a) = 3, razón común (r) = (3/2)/3 = 1/2 y suma de términos (S n ) = 3069/512.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
=> 3069/512 = 3[1–(1/2) n ] / [1–(1/2)]
=> 2(2 n –1)/(2 n ) = 1023/512
=> 1023(2) n = 1024(2) n – 1024
=> 2 n = 1024
=> norte = 10
Por lo tanto, 10 términos del GP deben tomarse juntos para hacer 3069/512.
Pregunta 6. ¿Cuántos términos de la serie 2 + 6 + 18 + …. debe tomarse para que la suma sea igual a 728?
Solución:
Dado que GP tiene el primer término (a) = 2, razón común (r) = 6/2 = 3 y suma de términos (S n ) = 728.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
=> 728 = 2[3 n –1]/[3–1]
=> 3 n –1 = 728
=> 3 n = 729
=> norte = 6
Por lo tanto, 6 términos del GP deben tomarse juntos para que la suma sea igual a 728.
Pregunta 7. ¿Cuántos términos de la sucesión √3, 3, 3√3,… hay que tomar para hacer la suma 39+ 13√3 ?
Solución:
Dado que GP tiene el primer término (a) = 2, razón común (r) = 3/√3 = 1/√3 y suma de términos (S n ) = 39+ 13√3.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
=> 39+13√3 = √3[3 n/2 –1]/(√3–1)
=> (39+13√3)(√3–1) = √3(3 n/2 –1)
=> 39√3–39+39–13√3 = 3 (n+1)/2 –√3
=> 3 (n+1)/2 = 27√3
=> 3 n/2 √3 = 27√3
=> 3 n/2 = 27
=> n/2 = 3
=> norte = 6
Por lo tanto, se deben tomar 6 términos del GP para hacer la suma 39+ 13√3.
Pregunta 8. La suma de n términos del GP 3, 6, 12, … es 381. Encuentra el valor de n.
Solución:
Dado que GP tiene el primer término (a) = 3, razón común (r) = 6/3 = 2 y suma de términos (S n ) = 381.
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
=> 381 = 3(2 n –1)/(2–1)
=> 2 n – 1 = 127
=> 2 n = 128
=> norte = 7
Por lo tanto, el valor de n es 7.
Pregunta 9. La razón común de un GP es 3, y el último término es 486. Si la suma de estos términos es 728, encuentre el primer término.
Solución:
Dado que GP tiene razón común (r) = 3, último término (a n ) = 486 y suma de términos (S n ) = 728.
Sabemos que el término n de un GP está dado por a n = ar n-1 .
=> 486 = a(3) n-1
=> 486 = un(3) n /3
=> un(3) norte = 1458 . . . . (1)
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
=> 728 = a(3 n –1)/(3–1)
=> 1456 = a(3) n –a
Usando (1) en la ecuación, obtenemos,
=> un = 1458 – 1456 = 2
Por lo tanto, el primer término del GP es 2.
Pregunta 10. La razón de la suma de los primeros tres términos a la de los primeros 6 términos de un GP es 125: 152. Encuentra la razón común.
Solución:
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
De acuerdo con la pregunta, tenemos,
=>
=> (r 3 –1)/(r 6 –1) = 125/152
=> 1/( r3+ 1 ) = 125/152
=> 125r 3 + 125 = 152
=> r3 = 27/125
=> r = 3/5
Por lo tanto, la razón común es 3/5.
Pregunta 11. Los términos 4 y 7 de un GP son 1/27 y 1/729 respectivamente. Encuentre la suma de n términos del GP
Solución:
Sabemos que el término n de un GP está dado por a n = ar n-1 .
De acuerdo con la pregunta, tenemos,
=> ar 3 = 1/27 . . . . (1)
=> ar 6 = 1/729 . . . . (2)
Dividiendo (2) por (1), obtenemos,
=> r3 = 27/729 = 1/27
=> r = 1/3
Poniendo r = 1/3 en (1), obtenemos,
=> un(1/3) 3 = 1/27
=> un(1/27) = 1/27
=> un = 1
Sabemos que la suma de n términos de un GP está dada por S n = a(r n –1)/(r–1).
=> S norte = 1[(1/3) norte –1]/[(1/3)–1]
= 3[1–(1/3) n ]/2
Por lo tanto, la suma de n términos del GP es 3[1–(1/3) n ]/2.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com (a^2-b^2)\left[\frac{1-(\frac{1}{a+b})^n}{1-(\frac{1}{a+b})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1cb4ce8a57dbeae8883b023297b3dfe2_l3.png)

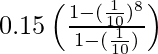
![Rendered by QuickLaTeX.com \frac{2}{9}\left[\frac{(\frac{3}{2})^5-1}{\frac{3}{2}-1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d24d9742dd4b4b99c6f1a7e229bddd98_l3.png)
![Rendered by QuickLaTeX.com \frac{3}{5}\left[\frac{(\frac{1}{25})^n-1}{(\frac{1}{25})-1}\right]+\frac{4}{25}\left[\frac{(\frac{1}{25})^n-1}{(\frac{1}{25})-1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-233461a2ff98c9439785c5b73dc938f8_l3.png)
![Rendered by QuickLaTeX.com \frac{a}{1+i}\left[\frac{1-(\frac{1}{1+i})^n}{1-\frac{1}{1+i}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-06e1f606f4cd3c9f353cd7a12ddadd65_l3.png)
![Rendered by QuickLaTeX.com \frac{5}{9}\left[n-\frac{(\frac{1}{10})(1-(\frac{1}{10})^n}{1-\frac{1}{10}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7fb61eced455a53801979f113f541eeb_l3.png)
![Rendered by QuickLaTeX.com \frac{6}{9}\left[n-\frac{(\frac{1}{10})(1-(\frac{1}{10})^n}{1-\frac{1}{10}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3b8b6859ebd50d5e71cf1a3819afe7c_l3.png)
