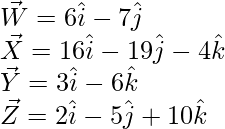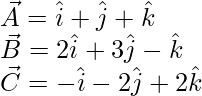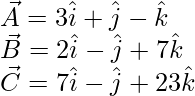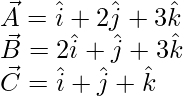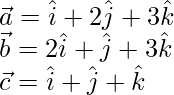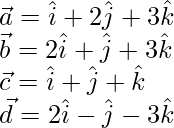Clase 12 RD Sharma- Capítulo 23 Álgebra de Vectores – Ejercicio 23.8

Pregunta 1. Muestre que los puntos cuyos vectores de posición se dan son colineales:

(i) 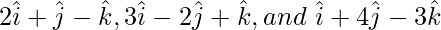$2\hat{i}+\hat{j}-\hat{k}, 3\hat{i}-2\hat{j}+\hat{k}, and \ \hat{i}+4\hat{j}-3\hat{k}$

Solución:

Sea x = $2\hat{i}+\hat{j}-\hat{k}$

y = $3\hat{i}-2\hat{j}+\hat{k}$

z = $\hat{i}+4\hat{j}-3\hat{k}$

Después

$\overrightarrow{xy}$ = Vector de posición de (y) – Vector de posición de (x)

= $3\hat{i}-2\hat{j}+\hat{k}-2\hat{i}-\hat{j}+\hat{k}$

= $\hat{i}-3\hat{j}+2\hat{k}$

$\overrightarrow{yz}$ = Vector de posición de (z) – Vector de posición de (y)

= $\hat{i}+4\hat{j}-3\hat{k} - 3\hat{i}+2\hat{j}-\hat{k}$

= $-2\hat{i}+6\hat{j}-4\hat{k}$

Como, $\overrightarrow{yz} = -2(\overrightarrow{xy})$

Entonces, $\overrightarrow{yz}$ y $\overrightarrow{xy}$ son vectores paralelos pero y es un punto común a ellos. Por lo tanto, los puntos dados x, y, z son colineales.

(ii) 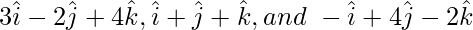$3\hat{i}-2\hat{j}+4\hat{k}, \hat{i}+\hat{j}+\hat{k}, and \ -\hat{i}+4\hat{j}-2\hat{k}$

Solución:

Dejar

x = $3\hat{i}-2\hat{j}+4\hat{k}$

y = $\hat{i}+\hat{j}+\hat{k}$

z = $-\hat{i}+4\hat{j}-2\hat{k}$

Después,

$\overrightarrow{xy}$ = Vector de posición de (y) – Vector de posición de (x)

= $\hat{i}+\hat{j}+\hat{k}-3\hat{i}+2\hat{j}-4\hat{k}$

= $-2\hat{i}+3\hat{j}-3\hat{k}$

$\overrightarrow{yz}$ = Vector de posición de (z) – Vector de posición de (y)

= $-\hat{i}+4\hat{j}-2\hat{k}-\hat{i}-\hat{j}-\hat{k}$

= $-2\hat{i}+3\hat{j}-3\hat{k}$

Como, $\overrightarrow{yz} = \overrightarrow{xy}$

Entonces, $\overrightarrow{yz}$ y $\overrightarrow{xy}$ son vectores paralelos pero y es un punto común a ellos. Por lo tanto, los puntos dados x, y, z son colineales.

Pregunta 2 (i). Usando el método vectorial, demuestre que A(6, -7, -1), B(2, -3, 1) y C(4, -5, 0) son colineales.

Solución:

Los puntos dados son A(6, -7, -1), B(2, -3, 1) y C(4, -5, 0)

Asi que, $\vec{A}=6\hat{i}-7\hat{j}-\hat{k}$

$\vec{B}=2\hat{i}-3\hat{j}+\hat{k}$

$\vec{C}=4\hat{i}-5\hat{j}$

$\overrightarrow{AB}$ = Vector de posición de (B) – Vector de posición de (A)

= $2\hat{i}-3\hat{j}+\hat{k}-6\hat{i}+7\hat{j}+\hat{k}$

= $-4\hat{i}+4\hat{j}+2\hat{k}$

$\overrightarrow{BC}$ = Vector de posición de (C) – Vector de posición de (B)

= $4\hat{i}-5\hat{j}-2\hat{i}+3\hat{j}-\hat{k}$

= $2\hat{i}-2\hat{j}-\hat{k}$

Como, $\overrightarrow{AB} = -2(\overrightarrow{BC})$

Entonces, $\overrightarrow{AB}$ y $\overrightarrow{BC}$ son vectores paralelos pero B es un punto común a ellos. Por lo tanto, los puntos dados A, B, C son colineales.

Pregunta 2 (ii). Usando el método vectorial, demuestre que A(2, -1, 3), B(4, 3, 1) y C(3, 1, 2) son colineales.

Solución:

Los puntos dados son A(2, -1, 3), B(4, 3, 1), C(3, 1, 2)

Entonces el $\vec{A}=2\hat{i}-\hat{j}+3\hat{k}$

$\vec{B}=4\hat{i}+3\hat{j}+\hat{k}$

$\vec{C}=3\hat{i}+\hat{j}+2\hat{k}$

$\overrightarrow{AB}$ = Vector de posición de (B) – Vector de posición de (A)

= $4\hat{i}+3\hat{j}+\hat{k}-2\hat{i}+\hat{j}-3\hat{k}$

= $2\hat{i}+4\hat{j}-2\hat{k}$

$\overrightarrow{BC}$ = Vector de posición de (C) – Vector de posición de (B)

= $3\hat{i}+\hat{j}+2\hat{k}-4\hat{i}-3\hat{j}-\hat{k}$

= $-\hat{i}-2\hat{j}+\hat{k}$

Como, $\overrightarrow{AB} = -2(\overrightarrow{BC})$

Entonces, $\overrightarrow{AB}$ y $\overrightarrow{BC}$ son vectores paralelos pero B es un punto común a ellos. Por lo tanto, los puntos dados A, B, C son colineales.

Pregunta 2 (iii). Usando el método vectorial, demuestre que X(1, 2, 7), Y(2, 6, 3) y Z(3, 10, -1) son colineales.

Solución:

Los puntos dados son X(1, 2, 7), Y(2, 6, 3), Z(3, 10, -1).

Entonces el $\vec{X}=\hat{i}+2\hat{j}+7\hat{k}$

$\vec{Y}=2\hat{i}+6\hat{j}+3\hat{k}$

$\vec{Z}=3\hat{i}+10\hat{j}-\hat{k}$

$\overrightarrow{XY}$ = Vector de posición de (Y) – Vector de posición de (X)

= $2\hat{i}+6\hat{j}+3\hat{k}-\hat{i}-2\hat{j}-7\hat{k}$

= $\hat{i}+4\hat{j}-4\hat{k}$

$\overrightarrow{YZ}$ = = Vector de posición de (Z) – Vector de posición de (Y)

= $3\hat{i}+10\hat{j}-\hat{k}-2\hat{i}-6\hat{j}-3\hat{k}$

= $\hat{i}+4\hat{j}-4\hat{k}$

Como, $\overrightarrow{YZ} = \overrightarrow{XY}$

Entonces, $\overrightarrow{YZ}$ y $\overrightarrow{XY}$ son vectores paralelos pero Y es un punto común a ellos. Por lo tanto, los puntos dados X, Y, Z son colineales.

Pregunta 2 (iv). Usando el método vectorial, demuestre que X(-3, -2, -5), Y(1, 2, 3) y Z(3, 4, 7) son colineales.

Solución:

Los puntos dados son X(-3, -2, -5), Y(1, 2, 3) y Z(3, 4, 7)

Asi que, $\vec{X}=-3\hat{i}-2\hat{j}-5\hat{k}$

$\vec{Y}=\hat{i}+2\hat{j}+3\hat{k}$

$\vec{Z}=3\hat{i}+4\hat{j}+7\hat{k}$

$\overrightarrow{XY}$ = Vector de posición de (Y) – Vector de posición de (X)

= $\hat{i}+2\hat{j}+3\hat{k}+3\hat{i}+2\hat{j}+5\hat{k}$

= $4\hat{i}+4\hat{j}+8\hat{k}$

$\overrightarrow{YZ}$ = = Vector de posición de (Z) – Vector de posición de (Y)

= $3\hat{i}+4\hat{j}+7\hat{k}-\hat{i}-2\hat{j}-3\hat{k}$

= $2\hat{i}+2\hat{j}+4\hat{k}$

Como, $\overrightarrow{YZ} = 2(\overrightarrow{XY})$

Entonces, $\overrightarrow{YZ}$ y $\overrightarrow{XY}$ son vectores paralelos pero Y es un punto común a ellos. Por lo tanto, los puntos dados X, Y, Z son colineales.

Pregunta 2 (v). Usando el método vectorial, demuestre que X(2, -1, 3), Y(3, -5, 1) y Z(-1, 11, 9) son colineales.

Solución:

$\vec{X}=2\hat{i}-\hat{j}+3\hat{k}$

$\vec{Y}=3\hat{i}-5\hat{j}+\hat{k}$

$\vec{Z}=-\hat{i}+11\hat{j}+9\hat{k}$

$\overrightarrow{XY}$ = Vector de posición de (Y) – Vector de posición de (X)

= $3\hat{i}-5\hat{j}+\hat{k}-2\hat{i}-\hat{j}+3\hat{k}$

= $\hat{i}-4\hat{j}-2\hat{k}$

$\overrightarrow{YZ}$ = = Vector de posición de (Z) – Vector de posición de (Y)

= $-\hat{i}+11\hat{j}+9\hat{k}-3\hat{i}+5\hat{j}-\hat{k}$

= $-4\hat{i}+16\hat{j}+8\hat{k}$

Como, $\overrightarrow{YZ} = 4(\overrightarrow{XY})$

Entonces, $\overrightarrow{YZ}$ y $\overrightarrow{XY}$ son vectores paralelos pero Y es un punto común a ellos. Por lo tanto, los puntos dados X, Y, Z son colineales.

Pregunta 3 (i). Si 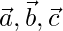$\vec{a},\vec{b},\vec{c}$ son vectores distintos de cero y no coplanares, demuestre que los vectores 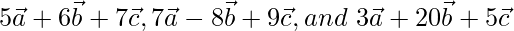$5\vec{a}+6\vec{b}+7\vec{c}, 7\vec{a}-8\vec{b}+9\vec{c}, and \ 3\vec{a}+20\vec{b}+5\vec{c}$ son coplanares.

Solución:

Los vectores dados son

X = $5\vec{a}+6\vec{b}+7\vec{c}$

Y = $7\vec{a}-8\vec{b}+9\vec{c}$

Z = $3\vec{a}+20\vec{b}+5\vec{c}$

Tres vectores son coplanares, si cumplen las condiciones dadas (para u y v reales)

X = tu * Y + v * Z

$5\vec{a}+6\vec{b}+7\vec{c}=u(7\vec{a}-8\vec{b}+9\vec{c})+v(3\vec{a}+20\vec{b}+5\vec{c})$

$5\vec{a}+6\vec{b}+7\vec{c}=\vec{a}(7u+3v)+\vec{b}(20v-8u)+\vec{c}(9u+5v)$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

7u + 3v = 5 -(1)

20v – 8u = 6 -(2)

9u + 5v = 7 -(3)

De las dos primeras ecuaciones, encontramos que

tu = 1/2

v = 1/2

Ahora ponga el valor de u y v en eq(3)

9(1/2) + 5(1/2) = 7

14/2 = 7

7 = 7

Entonces, el valor satisface la tercera ecuación.

Por tanto, los vectores dados X, Y, Z son coplanares.

Pregunta 3 (ii). Si 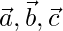$\vec{a},\vec{b},\vec{c}$ son vectores distintos de cero y no coplanares, demuestre que los vectores 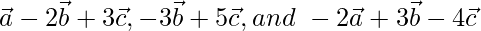$\vec{a}-2\vec{b}+3\vec{c}, -3\vec{b}+5\vec{c}, and \ -2\vec{a}+3\vec{b}-4\vec{c}$ son coplanares.

Solución:

Los vectores dados son

X = $\vec{a}-2\vec{b}+3\vec{c}$

Y = $-3\vec{b}+5\vec{c}$

Z = $-2\vec{a}+3\vec{b}-4\vec{c}$

Tres vectores son coplanares, si cumplen las condiciones dadas (para u y v reales)

X = tu * Y + v * Z

$\vec{a}-2\vec{b}+3\vec{c}=u(-3\vec{b}+5\vec{c})+v(-2\vec{a}+3\vec{b}-4\vec{c})$

$\vec{a}-2\vec{b}+3\vec{c}=(-2v)\vec{a} +\vec{b}(-3u+3v)+\vec{c}(5u-4v)$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

-2v = 1 -(1)

3v – 3u = -2 -(2)

5u – 4v = 3 -(3)

De las dos primeras ecuaciones, encontramos que

v = -1/2

tu = 1/6

Ahora ponga el valor de u y v en eq(3)

5(1/6) – 4(-1/2) = 3

5/6 + 2 = 3

(5 + 12)/6 = 3

17/6 ≠ 3

El valor no satisface la tercera ecuación. Por tanto, los vectores dados X, Y, Z no son coplanares.

Pregunta 4. Muestre que los cuatro puntos que tienen vectores de posición 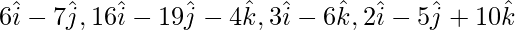$6\hat{i}-7\hat{j}, 16\hat{i}-19\hat{j}-4\hat{k},3\hat{i}-6\hat{k},2\hat{i}-5\hat{j}+10\hat{k}$ son coplanares.

Solución:

Sean los vectores dados

$\vec{W}=6\hat{i}-7\hat{j}\\ \vec{X}=16\hat{i}-19\hat{j}-4\hat{k}\\ \vec{Y}=3\hat{i}-6\hat{k}\\ \vec{Z}=2\hat{i}-5\hat{j}+10\hat{k}$

$\overrightarrow{WX}$ = Vector de posición de (X) – Vector de posición de (W)

= $16\hat{i}-19\hat{j}-4\hat{k} - 6\hat{i}+7\hat{j}$

= $10\hat{i}-12\hat{j}-4\hat{k}$

$\overrightarrow{WY}$ = Vector de posición de (Y) – Vector de posición de (W)

= $3\hat{i}-6\hat{k}- 6\hat{i}+7\hat{j}$

= $-3\hat{i}+7\hat{j}-6\hat{k}$

$\overrightarrow{WZ}$ = Vector de posición de (Z) – Vector de posición de (W)

= $2\hat{i}-5\hat{j}+10\hat{k} - 6\hat{i}+7\hat{j}$

= $-4\hat{i}+2\hat{j}+10\hat{k}$

Los vectores dados son coplanares si,

WX = u(WY) + v(WZ)

$10\hat{i}-12\hat{j}-4\hat{k}=u(-6\hat{i}+10\hat{j}-6\hat{k})+v(-4\hat{i}+2\hat{j}+10\hat{k})$

$10\hat{i}-12\hat{j}-4\hat{k}=\hat{i}(-6u-4v)+\hat{j}(10u+2v)+\hat{k}(-6u+10v)$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

-6u – 4v = 10 -(1)

10u + 2v = -12 -(2)

-6u + 10v = -4 -(3)

De las dos primeras ecuaciones, encontramos que

tu = -1

v = -1

Ahora ponga el valor de u y v en eq(3)

-6(-1) + 10(-1) = -4

6 – 10 = -4

-4 = -4

El valor satisface la tercera ecuación. Por tanto, los vectores dados W, X, Y, Z son coplanares.

Pregunta 5(i). Demostrar que los siguientes vectores son coplanares Demostrar que los puntos 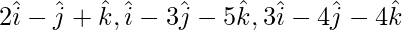$2\hat{i}-\hat{j}+\hat{k},\hat{i}-3\hat{j}-5\hat{k},3\hat{i}-4\hat{j}-4\hat{k}$

Solución:

Los vectores dados son $\vec{A}=2\hat{i}-\hat{j}+\hat{k}\\ \vec{B}=\hat{i}-3\hat{j}-5\hat{k}\\ \vec{C}=3\hat{i}-4\hat{j}-4\hat{k}$

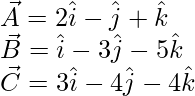
Los vectores dados son coplanares si,

A = u(B) + v(C)

$2\hat{i}-\hat{j}+\hat{k}=u(\hat{i}-3\hat{j}-5\hat{k})+v(3\hat{i}-4\hat{j}-4\hat{k})$

$2\hat{i}-\hat{j}+\hat{k}=\hat{i}(u+3v)+\hat{j}(-3u-4v)+\hat{k}(-5u-4v)$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

u + 3v = 2 -(1)

-3u – 4v = -1 -(2)

-5u – 4v = 1 -(3)

De las dos primeras ecuaciones, encontramos que

tu = -1

v = 1

Ahora ponga el valor de u y v en eq(3)

-5(-1) – 4(1) = 1

5 – 4 = 1

1 = 1

El valor satisface la tercera ecuación. Por tanto, los vectores dados A, B, C son coplanares.

Pregunta 5(ii). Demostrar que los siguientes vectores son coplanares Demostrar que los puntos 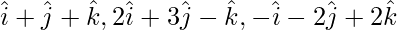$\hat{i}+\hat{j}+\hat{k},2\hat{i}+3\hat{j}-\hat{k},-\hat{i}-2\hat{j}+2\hat{k}$

Solución:

Los vectores dados son $\vec{A}=\hat{i}+\hat{j}+\hat{k}\\ \vec{B}=2\hat{i}+3\hat{j}-\hat{k}\\ \vec{C}=-\hat{i}-2\hat{j}+2\hat{k}$

Los vectores dados son coplanares si,

A = u(B) + v(C)

$\hat{i}+\hat{j}+\hat{k}=u(2\hat{i}+3\hat{j}-\hat{k})+v(-\hat{i}-2\hat{j}+2\hat{k})$

$\hat{i}+\hat{j}+\hat{k}=(2u-v)\hat{i}+(3u-2v)\hat{j}+(-u+2v)\hat{k}$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

2u – v = 1 -(1)

3u – 2v = 1 -(2)

-u + 2v = 1 -(3)

De las dos primeras ecuaciones, encontramos que

tu = 1

v = 1

Ahora ponga el valor de u y v en eq(3)

-(1) + 2(1) = 1

1 = 1

El valor satisface la tercera ecuación. Por tanto, los vectores dados A, B, C son coplanares.

Pregunta 6 (i). Demostrar que los vectores 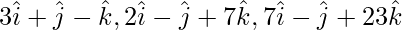$3\hat{i}+\hat{j}-\hat{k},2\hat{i}-\hat{j}+7\hat{k},7\hat{i}-\hat{j}+23\hat{k}$ no son coplanares.

Solución:

Los vectores dados son $\vec{A}=3\hat{i}+\hat{j}-\hat{k}\\ \vec{B}=2\hat{i}-\hat{j}+7\hat{k}\\ \vec{C}=7\hat{i}-\hat{j}+23\hat{k}$

Los vectores dados son coplanares si,

A = u(B) + v(C)

$3\hat{i}+\hat{j}-\hat{k}=u(2\hat{i}-\hat{j}+7\hat{k})+v(7\hat{i}-\hat{j}+23\hat{k})$

$3\hat{i}+\hat{j}-\hat{k}=(2u+7v)\hat{i}+(-u-v)\hat{j}+(7u+23v)\hat{k}$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

2u + 7v = 3 -(1)

-u – v = 1 -(2)

7u + 23v = -1 -(3)

De las dos primeras ecuaciones, encontramos que

tu = -2

v = 1

Ahora ponga el valor de u y v en eq(3)

7(-2) + 23(1) = -1

-14 + 23 = -1

-9 ≠ -1

El valor no satisface la tercera ecuación. Por tanto, los vectores dados A, B, C no son coplanares.

Pregunta 6 (ii). Demostrar que los vectores 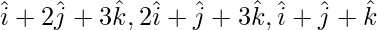$\hat{i}+2\hat{j}+3\hat{k},2\hat{i}+\hat{j}+3\hat{k},\hat{i}+\hat{j}+\hat{k}$ no son coplanares.

Solución:

Los vectores dados son $\vec{A}=\hat{i}+2\hat{j}+3\hat{k}\\ \vec{B}=2\hat{i}+\hat{j}+3\hat{k}\\ \vec{C}=\hat{i}+\hat{j}+\hat{k}$

Los vectores dados son coplanares si,

A = u(B) + v(C)

$\hat{i}+2\hat{j}+3\hat{k}=u(2\hat{i}+\hat{j}+3\hat{k})+v(\hat{i}+\hat{j}+\hat{k})$

$\hat{i}+2\hat{j}+3\hat{k}=(2u+v)\hat{i}+(u+v)\hat{j}+(3u+v)\hat{k}$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

2u + v = 1 -(1)

u + v = 2 -(2)

3u + v = 3 -(3)

De las dos primeras ecuaciones, encontramos que

tu = 0

v = 1

Ahora ponga el valor de u y v en eq(3)

3(0) + 1 = 3

1 = 3

El valor no satisface la tercera ecuación. Por tanto, los vectores dados A, B, C no son coplanares.

Pregunta 7(i). Si 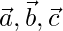$\vec{a},\vec{b},\vec{c}$ son vectores no coplanares, demuestre que los vectores dados no son coplanares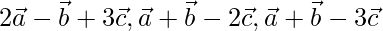 $2\vec{a}-\vec{b}+3\vec{c},\vec{a}+\vec{b}-2\vec{c},\vec{a}+\vec{b}-3\vec{c}$

Solución:

Los vectores dados son $D(2\vec{a}-\vec{b}+3\vec{c}),E(\vec{a}+\vec{b}-2\vec{c}),F(\vec{a}+\vec{b}-3\vec{c})$ )

Los vectores dados son coplanares si,

D = u(E) + v(F)

$2\vec{a}-\vec{b}+3\vec{c}=u(\vec{a}+\vec{b}-2\vec{c})+v(\vec{a}+\vec{b}-3\vec{c})$

$2\vec{a}-\vec{b}+3\vec{c}=(u+v)\vec{a}+(u+v)\vec{b}+(-2u-3v)\vec{c}$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

u + v = 2 -(1)

u + v = -1 -(2)

-2u – 3v = 3 -(3)

No hay ningún valor que satisfaga la tercera ecuación. Por tanto, los vectores dados D, E, F no son coplanares.

Pregunta 7(ii). Si 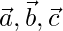$\vec{a},\vec{b},\vec{c}$ son vectores no coplanares, demuestre que los vectores dados no son coplanares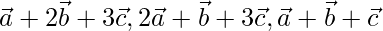 $\vec{a}+2\vec{b}+3\vec{c}, 2\vec{a}+\vec{b}+3\vec{c},\vec{a}+\vec{b}+\vec{c}$

Solución:

Los vectores dados son $D(\vec{a}+2\vec{b}+3\vec{c}),E(2\vec{a}+\vec{b}+3\vec{c}),F(\vec{a}+\vec{b}+\vec{c})$

Los vectores dados son coplanares si,

D = u(E) + v(F)

$\vec{a}+2\vec{b}+3\vec{c}=u(2\vec{a}+\vec{b}+3\vec{c})+v(\vec{a}+\vec{b}+\vec{c})$

$\vec{a}+2\vec{b}+3\vec{c}=(2u+v)\vec{a}+(u+v)\vec{b}+(3u+v)\vec{c}$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

2u + v = 1 -(1)

u + v = 2 -(2)

3u + v = 3 -(3)

De las dos primeras ecuaciones, encontramos que

tu = -1

v = 3

Ahora ponga el valor de u y v en eq(3)

3(-1) + (3) = 3

0 = 3

No hay ningún valor que satisfaga la tercera ecuación. Por tanto, los vectores dados D, E, F no son coplanares.

Pregunta 8. Demuestre que los vectores 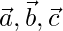$\vec{a},\vec{b},\vec{c}$ dados por 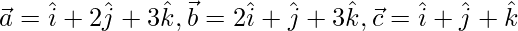$\vec{a}=\hat{i}+2\hat{j}+3\hat{k},\vec{b}=2\hat{i}+\hat{j}+3\hat{k},\vec{c}=\hat{i}+\hat{j}+\hat{k}$ no son coplanares. Exprese el vector \vec{d} = 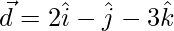$\vec{d} = 2\hat{i} -\hat{j}-3\hat{k}$ como una combinación lineal del vector $\vec{a},\vec{b}, and\ \vec{c}$ .

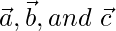Solución:

Los vectores dados son

$\vec{a}=\hat{i}+2\hat{j}+3\hat{k}\\ \vec{b}=2\hat{i}+\hat{j}+3\hat{k}\\ \vec{c}=\hat{i}+\hat{j}+\hat{k}$

Los vectores dados son coplanares si,

D = u(E) + v(F)

Al comparar los coeficientes, obtenemos las siguientes ecuaciones

2u + v = 1 -(1)

u + v = 2 -(2)

3u + v = 3 -(3)

De las dos ecuaciones anteriores,

tu = -1

v = 3

Ahora ponga el valor de u y v en eq(3)

3(-1) + (3) = 3

0 = -3

No hay ningún valor que satisfaga la tercera ecuación. Por lo tanto, los vectores dados D, E, F no son coplanares

Los vectores dados son

$\vec{a}=\hat{i}+2\hat{j}+3\hat{k}\\ \vec{b}=2\hat{i}+\hat{j}+3\hat{k}\\ \vec{c}=\hat{i}+\hat{j}+\hat{k}\\ \vec{d}=2\hat{i}-\hat{j}-3\hat{k}$

Los vectores dados son coplanares si,

$\vec{d}=\vec{a}x+\vec{b}y+\vec{c}z$

$2\hat{i}-\hat{j}-3\hat{k}=x(\hat{i}+2\hat{j}+3\hat{k})+y(2\hat{i}+\hat{j}+3\hat{k})+z(\hat{i}+\hat{j}+\hat{k})$

$2\hat{i}-\hat{j}-3\hat{k}=(x+2y+z)\hat{i}+(2x+y+z)\hat{j}+(3x+3y+z)\hat{k}$

Al comparar los coeficientes, obtenemos las siguientes ecuaciones,

x + 2y + z = 2 -(1)

2x + y + z = -1 -(2)

3x + 3y + z = -3 -(3)

De las tres ecuaciones anteriores,

x = -8/3

y = 1/3

z = 4

Por lo tanto, $\vec{d} = \frac{-8}{3}\vec{a} + \frac{1}{3}\vec{b} + 4\vec{c}$

Pregunta 9. Demostrar que una condición necesaria y suficiente para que los tres vectores 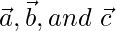$\vec{a},\vec{b},and \ \vec{c}$ sean coplanares es que estos existan escalares l, m, n, no todos cero simultáneamente tal que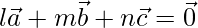 $l\vec{a}+m\vec{b}+n\vec{c} = \vec{0}$

Solución:

Condiciones dadas: Consideremos $\vec{a},\vec{b},and \ \vec{c}$ tres vectores coplanares.

Entonces uno de ellos es expresable como combinación lineal de otros dos vectores.

Dejar,

$c=x\vec{a} +y\vec{b}$

$x\vec{a}+y\vec{b}-\vec{c}=0$

Aquí, l = x, y = m, n = -1

Desde arriba,

$l\vec{a}+m\vec{b}+n\vec{c}=0$

$n\vec{c}=-l\vec{a}-m\vec{b}$

$\vec{c}=(-l/n)\vec{a}+(-m/n)\vec{b}$

Por lo tanto, $\vec{c}$ es una combinación lineal de dos vectores $\vec{a} \ and \ \vec{b}$ .

Por lo tanto, se demostró que $\vec{a},\vec{b},and \ \vec{c}$ son vectores coplanares.

Pregunta 10. Muestre que los cuatro puntos A, B, C y D con vectores de posición 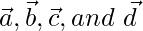$\vec{a},\vec{b},\vec{c}, and \ \vec{d}$ respectivamente son coplanares si y solo si $3\vec{a}-2\vec{b}+\vec{c}-2\vec{d} = 0$ .

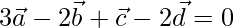Solución:

Dado: A, B, C, D ser cuatro vectores con vector de posición $\vec{a},\vec{b},\vec{c}, and \ \vec{d}$

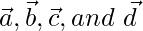
Consideremos que A, B, C, D son coplanares.

Entonces, existe x, y, z, u no todo cero tal que,

$x\vec{a} + y\vec{b} + z\vec{c} + u\vec{d} = 0$

Consideremos x = 3, y = -2, z = 1, y = -2

Asi que, $3\vec{a}-2\vec{b}+\vec{c}-2\vec{d}=0$

y x + y + z + u = 3 – 2 + 1 – 2 = 0

Entonces, A, B, C, D son coplanares.

Consideremos $3\vec{a}-2\vec{b}+\vec{c}-2\vec{d}=0$

$3\vec{a}+\vec{c}=2\vec{b}+2\vec{d}$

Ahora al dividir ambos lados por la suma del coeficiente 4

$\frac{(3\vec{a}+\vec{c})}{4}=\frac{(2\vec{b}+2\vec{d})}{4}$

$\frac{(3\vec{a}+\vec{c})}{(3+1)}=\frac{(2\vec{b}+2\vec{d})}{(2+2)}$

Muestra que el punto P divide internamente AC en la razón 1:3 y BD en la razón 2:2,

por tanto, P es el punto de intersección de AC y BD.

Entonces, A, B, C, D son coplanares.

Publicación traducida automáticamente

Artículo escrito por neeraj kumar 13 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Muestre que los puntos cuyos vectores de posición se dan son colineales:

(i)

(ii)

Pregunta 2 (i). Usando el método vectorial, demuestre que A(6, -7, -1), B(2, -3, 1) y C(4, -5, 0) son colineales.

Pregunta 2 (ii). Usando el método vectorial, demuestre que A(2, -1, 3), B(4, 3, 1) y C(3, 1, 2) son colineales.

Pregunta 2 (iii). Usando el método vectorial, demuestre que X(1, 2, 7), Y(2, 6, 3) y Z(3, 10, -1) son colineales.

Pregunta 2 (iv). Usando el método vectorial, demuestre que X(-3, -2, -5), Y(1, 2, 3) y Z(3, 4, 7) son colineales.

Pregunta 2 (v). Usando el método vectorial, demuestre que X(2, -1, 3), Y(3, -5, 1) y Z(-1, 11, 9) son colineales.

Pregunta 3 (i). Si son vectores distintos de cero y no coplanares, demuestre que los vectores son coplanares.

Pregunta 3 (ii). Si son vectores distintos de cero y no coplanares, demuestre que los vectores son coplanares.

Pregunta 4. Muestre que los cuatro puntos que tienen vectores de posición son coplanares.

Pregunta 5(i). Demostrar que los siguientes vectores son coplanares Demostrar que los puntos

Pregunta 5(ii). Demostrar que los siguientes vectores son coplanares Demostrar que los puntos

Pregunta 6 (i). Demostrar que los vectores no son coplanares.

Pregunta 6 (ii). Demostrar que los vectores no son coplanares.

Pregunta 7(i). Si son vectores no coplanares, demuestre que los vectores dados no son coplanares

Pregunta 7(ii). Si son vectores no coplanares, demuestre que los vectores dados no son coplanares

Pregunta 8. Demuestre que los vectores dados por no son coplanares. Exprese el vector \vec{d} = como una combinación lineal del vector .

Pregunta 9. Demostrar que una condición necesaria y suficiente para que los tres vectores sean coplanares es que estos existan escalares l, m, n, no todos cero simultáneamente tal que

Pregunta 10. Muestre que los cuatro puntos A, B, C y D con vectores de posición respectivamente son coplanares si y solo si .

Deja una respuesta Cancelar la respuesta

(i) $2\hat{i}+\hat{j}-\hat{k}, 3\hat{i}-2\hat{j}+\hat{k}, and \ \hat{i}+4\hat{j}-3\hat{k}$

(ii) $3\hat{i}-2\hat{j}+4\hat{k}, \hat{i}+\hat{j}+\hat{k}, and \ -\hat{i}+4\hat{j}-2\hat{k}$

Pregunta 3 (i). Si $\vec{a},\vec{b},\vec{c}$ son vectores distintos de cero y no coplanares, demuestre que los vectores $5\vec{a}+6\vec{b}+7\vec{c}, 7\vec{a}-8\vec{b}+9\vec{c}, and \ 3\vec{a}+20\vec{b}+5\vec{c}$ son coplanares.

Pregunta 3 (ii). Si $\vec{a},\vec{b},\vec{c}$ son vectores distintos de cero y no coplanares, demuestre que los vectores $\vec{a}-2\vec{b}+3\vec{c}, -3\vec{b}+5\vec{c}, and \ -2\vec{a}+3\vec{b}-4\vec{c}$ son coplanares.

Pregunta 4. Muestre que los cuatro puntos que tienen vectores de posición $6\hat{i}-7\hat{j}, 16\hat{i}-19\hat{j}-4\hat{k},3\hat{i}-6\hat{k},2\hat{i}-5\hat{j}+10\hat{k}$ son coplanares.

Pregunta 5(i). Demostrar que los siguientes vectores son coplanares Demostrar que los puntos $2\hat{i}-\hat{j}+\hat{k},\hat{i}-3\hat{j}-5\hat{k},3\hat{i}-4\hat{j}-4\hat{k}$

Pregunta 5(ii). Demostrar que los siguientes vectores son coplanares Demostrar que los puntos $\hat{i}+\hat{j}+\hat{k},2\hat{i}+3\hat{j}-\hat{k},-\hat{i}-2\hat{j}+2\hat{k}$

Pregunta 6 (i). Demostrar que los vectores $3\hat{i}+\hat{j}-\hat{k},2\hat{i}-\hat{j}+7\hat{k},7\hat{i}-\hat{j}+23\hat{k}$ no son coplanares.

Pregunta 6 (ii). Demostrar que los vectores $\hat{i}+2\hat{j}+3\hat{k},2\hat{i}+\hat{j}+3\hat{k},\hat{i}+\hat{j}+\hat{k}$ no son coplanares.

Pregunta 7(i). Si $\vec{a},\vec{b},\vec{c}$ son vectores no coplanares, demuestre que los vectores dados no son coplanares $2\vec{a}-\vec{b}+3\vec{c},\vec{a}+\vec{b}-2\vec{c},\vec{a}+\vec{b}-3\vec{c}$

Pregunta 7(ii). Si $\vec{a},\vec{b},\vec{c}$ son vectores no coplanares, demuestre que los vectores dados no son coplanares $\vec{a}+2\vec{b}+3\vec{c}, 2\vec{a}+\vec{b}+3\vec{c},\vec{a}+\vec{b}+\vec{c}$

Pregunta 9. Demostrar que una condición necesaria y suficiente para que los tres vectores $\vec{a},\vec{b},and \ \vec{c}$ sean coplanares es que estos existan escalares l, m, n, no todos cero simultáneamente tal que $l\vec{a}+m\vec{b}+n\vec{c} = \vec{0}$

Pregunta 10. Muestre que los cuatro puntos A, B, C y D con vectores de posición $\vec{a},\vec{b},\vec{c}, and \ \vec{d}$ respectivamente son coplanares si y solo si $3\vec{a}-2\vec{b}+\vec{c}-2\vec{d} = 0$ .