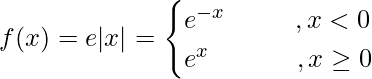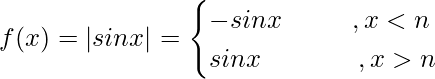Clase 12 Soluciones RD Sharma – Capítulo 10 Diferenciabilidad – Ejercicio 10.2

Pregunta 1. Si f está definida por f(x) = x ² , encuentre f'(2).

Solución:

$f'(2) = lim_{h\to0}\frac{f(2+h)-f(2)}{h}$

$= lim_{h\to0}\frac{(2+h)^2-2^2}{h}$

$= lim_{h\to0}\frac{4+h^2+4h-4}{h}$

$= lim_{h\to0}(4+h)$

Por lo tanto, f'(2) = 4.

Pregunta 2. Si f está definida por f(x) = x ² – 4x + 7, demuestre que f'(5) = 2f'(7/2).

Solución:

$f'(5) = lim_{h\to0}\frac{f(5+h)-f(5)}{h}$

= $lim_{h\to0}\frac{((5+h^2)-4(5+h)+7)-(25-20+7)}{h}$

$= lim_{h\to0}\frac{h^2+25+10h-20-4h+7-12}{h}$

$= lim_{h\to0}\frac{h^2+6h}{h}$

f'(5) = 6 …….(1)

$f'(7/2) = lim_{h\to0}\frac{f(7/2+h)-f(7/2)}{h}$

$= lim_{h\to0}\frac{h^2+7h-14-4h+7+14-7}{h}$

$= lim_{h\to0}\frac{h^2+3h}{h}$

$= lim_{h\to0}(h+3)$

f'(7/2) = 3

⇒ 2f'(7/2) = 6 ……(2)

De (1) y (2)

f'(5) = 2f'(7/2).

Pregunta 3. Muestre que la derivada de la función f dada por f(x) = 2x ³ – 9x ² +12x + 9 en x = 1 y x = 2 son iguales.

Solución:

$f'(1) = lim_{h\to0}\frac{f(1+h)-f(1)}{h}$

$= lim_{h\to0}\frac{[2(1+h)^2-9(1+h)^2+12(1+h)+9]-[2-9+12-9]}{h}$

$= lim_{h\to0}\frac{2+2h^3+6h^2+6h-9-9h^2-18h+12+12h+9-14}{h}$

$= lim_{h\to0}\frac{2h^3-3h^2}{h}$

$= lim_{h\to0}h(2h-3)$

⇒ f'(1) = 0

Ahora, $f'(2) = lim_{h\to0}\frac{f(2+h)-f(2)}{h}$

$= lim_{h\to0}\frac{[2(2+h)^3-9(2+h)^2+12(2+h)+9]-[16-36+24+9]}{h}$

$= lim_{h\to0}\frac{2h^3-3h^2}{h}$

$= lim_{h\to0}h(2h-3)$

⇒ f'(2) = 0

Por lo tanto f'(1) = f'(2) = 0.

Pregunta 4. Si para la función f(x) = ax ² + 7x – 4, f'(5) = 97, encuentra a.

Solución:

$f'(5) = lim_{h\to0}\frac{f(5+h)-f(5)}{h}$

$⇒ 97 = lim_{h\to0}\frac{a(25+h^2+10h)+35+7h-4-25a-35+4}{h}$

$= lim_{h\to0}\frac{25a+ah^2+10ah-25a+7h}{h}$

$= lim_{h\to0}\frac{ah^2+h(10a+7)}{h}$

⇒ 97 = 10a +7

⇒ 10a = 90

⇒ un = 9

Pregunta 5. Si f(x) = x ³ + 7x ² + 8x – 9, encuentra f'(4).

Solución:

$f'(4) = lim_{h\to0}\frac{f(4+h)-f(4)}{h}$

$= lim_{h\to0}\frac{[(4+h)^3+7(4+h)^2+8(4+h)-9]-[64+112+32-9]}{h}$

$= lim_{h\to0}\frac{64+h^3+48h+12h^2+112+7h^2+56h+32+8h-9]-[210-9]}{h}$

$= lim_{h\to0}\frac{h^3+19h^2+112h}{h}$

$= lim_{h\to0}\frac{h(h^2+19h+112)}{h}$

⇒ f'(4) = 112

Pregunta 6. Encuentra la derivada de f(x) = mx + c en x = 0.

Solución:

$f'(0) = lim_{h\to0}\frac{f(0+h)-f(0)}{h}$

$= lim_{h\to0}\frac{f(h)-h(0)}{h}$

$= lim_{h\to0}\frac{(mh+c)-(c)}{h}$

$= lim_{h\to0}\frac{mh+c-c}{h}$

$= lim_{h\to0}\frac{mh}{h}$

⇒ f'(0) = m.

Pregunta 7. Examine la diferenciabilidad de $f(x) = \begin{cases}2x+3\ \ \ \ \ \ \ ,-3\lex<-2\\x+1\ \ \ \ \ \ \ \ \ ,-2\lex<0\\x+2\ \ \ \ \ \ \ \ \ ,0\lex1\end{cases}.$

Solución:

Dado que f(x) es una función polinomial, es continua y derivable en todas partes.

Diferenciabilidad en x = –2

$(LHD at x = -2) = lim_{h\to-2^-}\frac{f(x)-f(-2)}{x-(-2)}$

$= lim_{h\to-2^-}\frac{2x+3+1}{x+2}$

$= lim_{h\to-2^-}\frac{2(x+2)}{x+2}$

= 2

$(RHD at x = -2) = lim_{h\to-2^+}\frac{f(x)-f(-2)}{x-(-2)}$

$= lim_{h\to-2^-}\frac{x+1+1}{x+2}$

$= lim_{h\to-2^-}\frac{x+2}{x+2}$

= 1

Dado que LHD en x = –2 ≠ RHD en x = –2

Por tanto, f(x) no es diferenciable en x = –2.

Ahora, diferenciabilidad en x = 0

(LHD en x = 0) $= lim_{h\to0}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{x+1-2}{x}$

$= lim_{h\to0}\frac{x-1}{x}$

= ∞

(RHD en x = 0) $= lim_{h\to0}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{x+2-2}{x}$

$= lim_{h\to0}\frac{x}{x}$

= 1

Dado que LHD en x = –2 ≠ RHD en x = 0

Por tanto, f(x) no es diferenciable en x = 0.

Pregunta 8. Escriba un ejemplo de una función que sea continua en todas partes pero que no sea diferenciable en exactamente cinco puntos.

Solución:

Conocemos la función de módulo f(x) = |x| es continua pero no diferenciable en x = 0.

Por lo tanto, f(x) = |x| + |x – 1| + |x – 2| + |x – 3| + |x – 4| es continua pero no deja de ser diferenciable en x = 0,1,2,3,4.

Pregunta 9. Discuta la continuidad y diferenciabilidad de f(x) = |log|x||.

Solución:

Gráfica de f(x) = |log|x||:

Del gráfico anterior, está claro que f(x) es continua en todas partes, pero no diferenciable en 1 y -1.

Pregunta 10. Discuta la continuidad y diferenciabilidad de f(x) = e ^|x|.

Solución:

$f(x) = e|x| = \begin{cases}e^{-x} \ \ \ \ \ \ \ \ ,x<0\\e^x\ \ \ \ \ \ \ \ \ \ ,x\ge 0\end{cases}$

Para la continuidad:

(HL en x = 0) $= lim_{x\to0^-}f(x)$

= $lim_{h\to0}f(0-h)$

$= lim_{h\to0}e^{0-h}$

$= lim_{h\to0}e^{-h}$

= mi ⁰

= 1

(LH en x = 0) $= lim_{x\to0^+}f(x)$

$= lim_{h\to0}f(0+h)$

$= lim_{h\to0}e^{0+h}$

$= lim_{h\to0}e^h$

= mi ⁰

= 1

Por tanto, f(x) es continua en x = 0.

Por diferenciabilidad:

(LHD en x = 0) = $lim_{x\to0^-}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{e^h-1}{-h}$

= –1

(RHD en x = 0) $= lim_{x\to0^+}\frac{f(x)-f(0)}{x-0}$

$= lim_{h\to0}\frac{e^h-1}{h}$

= 1

Por tanto, f(x) no es diferenciable en x = 0.

Pregunta 11. Discuta la diferenciabilidad de 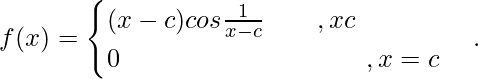$f(x) = \begin{cases}(x-c)cos\frac{1}{x-c}\ \ \ \ \ \ ,x≠c\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=c\end{cases}.$

Solución:

(LHD en x = c) $= lim_{x\to c^-}\frac{f(c-h)-f(c)}{-h}$

$= lim_{h\to0}\frac{cos(-1/h)}{h}$

$= lim_{h\to0}\frac{cos(1/h)}{h}$

= k

(RHD en x = c) = $lim_{x\to c^+}\frac{f(c+h)-f(c)}{h}$

$= lim_{h\to0}\frac{cos(1/h)}{h}$

= k

Claramente (LHD en x = c) = (RHD en x = c)

f(x) es diferenciable en x = c.

Pregunta 12. ¿Es |senx| diferenciable? ¿Qué hay de cos|x|?

Solución:

$f(x) = |sinx| = \begin{cases}-sinx \ \ \ \ \ \ \ \ , x<nπ\\sinx \ \ \ \ \ \ \ \ \ \ \ ,x>nπ\end{cases}$

(LHD en x = nπ) $= lim_{x\to nπ^-}\frac{f(x)-f(nπ)}{x-nπ}$

$= lim_{h\to0}\frac{-sin(nπ-h)-sinnπ}{nπ-h-nπ}$

$= lim_{h\to0}\frac{sinh}{-h}$

= –1

(RHD en x = nπ) $= lim_{h\to0}\frac{sin(nπ+h)-sinnπ}{h}$

$= lim_{h\to0}\frac{sinh}{-h}$

= 1

Dado que LHD en x = nπ ≠ RHD en x = nπ

Por lo tanto f(x) = |senx| no es diferenciable en x = nπ.

Ahora, f(x) = cos|x|

Como, cos(–x) = cosx

Así, f(x) = cos x

Por lo tanto f(x) = cos|x| es diferenciable en todas partes.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Si f está definida por f(x) = x 2 , encuentre f'(2).

Pregunta 2. Si f está definida por f(x) = x 2 – 4x + 7, demuestre que f'(5) = 2f'(7/2).

Pregunta 3. Muestre que la derivada de la función f dada por f(x) = 2x 3 – 9x 2 +12x + 9 en x = 1 y x = 2 son iguales.

Pregunta 4. Si para la función f(x) = ax 2 + 7x – 4, f'(5) = 97, encuentra a.

Pregunta 5. Si f(x) = x 3 + 7x 2 + 8x – 9, encuentra f'(4).

Pregunta 6. Encuentra la derivada de f(x) = mx + c en x = 0.

Pregunta 7. Examine la diferenciabilidad de

Pregunta 8. Escriba un ejemplo de una función que sea continua en todas partes pero que no sea diferenciable en exactamente cinco puntos.

Pregunta 9. Discuta la continuidad y diferenciabilidad de f(x) = |log|x||.

Pregunta 10. Discuta la continuidad y diferenciabilidad de f(x) = e |x| .

Pregunta 11. Discuta la diferenciabilidad de

Pregunta 12. ¿Es |senx| diferenciable? ¿Qué hay de cos|x|?

Deja una respuesta Cancelar la respuesta

Pregunta 1. Si f está definida por f(x) = x ² , encuentre f'(2).

Pregunta 2. Si f está definida por f(x) = x ² – 4x + 7, demuestre que f'(5) = 2f'(7/2).

Pregunta 3. Muestre que la derivada de la función f dada por f(x) = 2x ³ – 9x ² +12x + 9 en x = 1 y x = 2 son iguales.

Pregunta 4. Si para la función f(x) = ax ² + 7x – 4, f'(5) = 97, encuentra a.

Pregunta 5. Si f(x) = x ³ + 7x ² + 8x – 9, encuentra f'(4).

Pregunta 7. Examine la diferenciabilidad de $f(x) = \begin{cases}2x+3\ \ \ \ \ \ \ ,-3\lex<-2\\x+1\ \ \ \ \ \ \ \ \ ,-2\lex<0\\x+2\ \ \ \ \ \ \ \ \ ,0\lex1\end{cases}.$

Pregunta 10. Discuta la continuidad y diferenciabilidad de f(x) = e ^|x|.

Pregunta 11. Discuta la diferenciabilidad de $f(x) = \begin{cases}(x-c)cos\frac{1}{x-c}\ \ \ \ \ \ ,x≠c\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=c\end{cases}.$