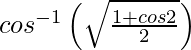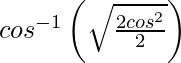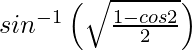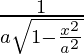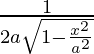Clase 12 Soluciones RD Sharma – Capítulo 11 Diferenciación – Ejercicio 11.3 | Serie 1

Posted on by Rudeus Greyrat

Pregunta 1. Diferenciar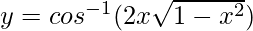y=cos^{-1}(2x\sqrt{1-x^2}) , 1/√2 < x < 1 con respecto a x.

Solución:

Tenemos,

y=cos^{-1}(2x\sqrt{1-x^2}) , 1/√2 < x < 1.

Al poner x = cos θ, obtenemos,

y =cos^{-1}(2cosθ\sqrt{1-cos^2θ})

=cos^{-1}(2cosθ\sqrt{sin^2θ})

= cos −1 (2 cos θ sen θ)

= cos −1 (sen 2θ)

=cos^{-1}(cos(\frac{π}{2}-2θ))

Ahora, 1/√2 < x < 1

=> 1/√2 < cos θ < 1

=> 0 < θ < π/4

=> 0 < 2θ < π/2

=> 0 > −2θ > −π/2

=> π/2 > (π/2−2θ) > 0

Entonces, y =\frac{π}{2}-2cos^{-1}x

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(\frac{π}{2}-2cos^{-1}x)

=0-2\left(\frac{-1}{\sqrt{1-x^2}}\right)

=\frac{2}{\sqrt{1-x^2}}

Pregunta 2. Diferenciar 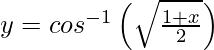y=cos^{-1}\left(\sqrt{\frac{1+x}{2}}\right) ,−1 < x < 1 con respecto a x.

Solución:

Tenemos, y=cos^{-1}\left(\sqrt{\frac{1+x}{2}}\right) ,−1 < x < 1.

Al poner x = cos 2θ, obtenemos,

y =cos^{-1}\left(\sqrt{\frac{1+cos2θ}{2}}\right)

=cos^{-1}\left(\sqrt{\frac{2cos^2θ}{2}}\right)

=cos^{-1}\left(\sqrt{cos^2θ}\right)

=cos^{-1}\left(cosθ\right)

Ahora, −1 < x < 1

=> −1 < cos 2θ < 1

=> 0 < 2θ < π

=> 0 < θ < π/2

Entonces, y =\frac{1}{2}cos^{-1}x

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(\frac{1}{2}cos^{-1}x)

=\frac{-1}{2\sqrt{1-x^2}}

Pregunta 3. Diferenciar 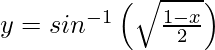y=sin^{-1}\left(\sqrt{\frac{1-x}{2}}\right) , 0 < x < 1 con respecto a x.

Solución:

Tenemos, y=sin^{-1}\left(\sqrt{\frac{1-x}{2}}\right) , 0 < x < 1.

Al poner x = cos 2θ, obtenemos,

y =sin^{-1}\left(\sqrt{\frac{1-cos2θ}{2}}\right)

=sin^{-1}\left(\sqrt{\frac{2sin^2θ}{2}}\right)

=sin^{-1}\left(sinθ\right)

Ahora, 0 < x < 1

=> 0 < cos 2θ < 1

=> 0 < 2θ < π/2

=> 0 < θ < π/4

Asi que,y = \frac{1}{2}cos^{-1}x

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(\frac{1}{2}cos^{-1}x)

=\frac{-1}{2\sqrt{1-x^2}}

Pregunta 4 . Deriva 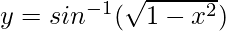y=sin^{-1}(\sqrt{1-x^2}) , 0 < x < 1 con respecto a x.

Solución:

Tenemos, y=sin^{-1}(\sqrt{1-x^2}) , 0 < x < 1

Al poner x = cos θ, obtenemos,

y =sin^{-1}(\sqrt{1-cos^2θ})

=sin^{-1}(\sqrt{sin^2θ})

=sin^{-1}\left(sinθ\right)

Ahora, 0 < x < 1

=> 0 < cos θ < 1

=> 0 < θ < π/2

Entonces, y = cos −1 x

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(cos^{-1}x)

=\frac{-1}{\sqrt{1-x^2}}

Pregunta 5. Diferenciar 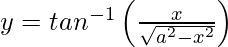y=tan^{-1}\left(\frac{x}{\sqrt{a^2-x^2}}\right) , −a < x < a con respecto a x.

Solución:

Tenemos, y=tan^{-1}\left(\frac{x}{\sqrt{a^2-x^2}}\right) , −a < x < a

Al poner x = a sen θ, obtenemos,

y =tan^{-1}\left(\frac{asinθ}{\sqrt{a^2-a^2sin^2θ}}\right)

=tan^{-1}\left(\frac{asinθ}{\sqrt{a^2cos^2θ}}\right)

=tan^{-1}\left(\frac{asinθ}{acosθ}\right)

=tan^{-1}\left(tanθ\right)

Ahora, −a < x < a

=> −1 < x/a < 1

=> −π/2 < θ < π/2

Asi que,y=sin^{-1}(\frac{x}{a})

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(sin^{-1}\frac{x}{a})

=\frac{1}{a\sqrt{1-\frac{x^2}{a^2}}}

=\frac{a}{a\sqrt{a^2-x^2}}

=\frac{1}{\sqrt{a^2-x^2}}

Pregunta 6. Diferenciar 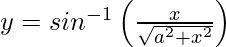y=sin^{-1}\left(\frac{x}{\sqrt{a^2+x^2}}\right) con respecto a x.

Solución:

Tenemos,y=sin^{-1}\left(\frac{x}{\sqrt{a^2+x^2}}\right)

Al poner x = a tan θ, obtenemos,

y =sin^{-1}\left(\frac{atanθ}{\sqrt{a^2+a^2tan^2θ}}\right)

=sin^{-1}\left(\frac{atanθ}{\sqrt{a^2sec^2θ}}\right)

=sin^{-1}\left(\frac{atanθ}{asecθ}\right)

=sin^{-1}(sinθ)

= θ

=tan^{-1}(\frac{x}{a})

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(tan^{-1}(\frac{x}{a}))

=\frac{1}{a(1+\frac{x^2}{a^2})}

=\frac{a^2}{a(a^2+x^2)}

=\frac{a}{\sqrt{a^2+x^2}}

Pregunta 7. Diferenciar 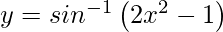y=sin^{-1}\left(2x^2-1\right) , 0 < x < 1 con respecto a x.

Solución:

Tenemos, y=sin^{-1}\left(2x^2-1\right) , 0 < x < 1

Al poner x = cos θ, obtenemos,

y =sin^{-1}\left(2cos^2θ-1\right)

=sin^{-1}\left(cos2θ\right)

=sin^{-1}\left(sin(\frac{π}{2}-2θ)\right)

Ahora, 0 < x < 1

=> 0 < cos θ < 1

=> 0 < θ < π/2

=> 0 < 2θ < π

=> π/2 > (π/2−2θ) > −π/2

Entonces, y =\frac{π}{2}-2cos^{-1}x

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(\frac{π}{2}-2cos^{-1}x)

=0-2\left(\frac{-1}{\sqrt{1-x^2}}\right)

=\frac{2}{\sqrt{1-x^2}}

Pregunta 8. Diferenciar 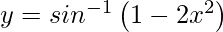y=sin^{-1}\left(1-2x^2\right) , 0 < x < 1 con respecto a x.

Solución:

Tenemos y=sin^{-1}\left(1-2x^2\right) , 0 < x < 1

Al poner x = sen θ, obtenemos,

y =sin^{-1}\left(1-2sin^2θ\right)

=sin^{-1}\left(cos2θ\right)

=sin^{-1}\left(sin(\frac{π}{2}-2θ)\right)

Ahora, 0 < x < 1

=> 0 < sen θ < 1

=> 0 < θ < π/2

=> 0 < 2θ < π

=> π/2 > (π/2−2θ) > −π/2

Entonces, y =\frac{π}{2}-2sin^{-1}x

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(\frac{π}{2}-2sin^{-1}x)

=0-2\left(\frac{1}{\sqrt{1-x^2}}\right)

=\frac{-2}{\sqrt{1-x^2}}

Pregunta 9. Diferenciar 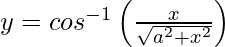y=cos^{-1}\left(\frac{x}{\sqrt{a^2+x^2}}\right) con respecto a x.

Solución:

Tenemos,y=cos^{-1}\left(\frac{x}{\sqrt{a^2+x^2}}\right)

Poniendo x = cot θ, obtenemos,

y =cos^{-1}\left(\frac{acotθ}{\sqrt{a^2+a^2cot^2θ}}\right)

=cos^{-1}\left(\frac{acotθ}{\sqrt{a^2cosec^2θ}}\right)

=cos^{-1}\left(\frac{acotθ}{acosecθ}\right)

=cos^{-1}(cosθ)

= θ

=cot^{-1}(\frac{x}{a})

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(cot^{-1}(\frac{x}{a}))

=\frac{-1}{a(1+\frac{x^2}{a^2})}

=\frac{-a^2}{a(a^2+x^2)}

=\frac{-a}{\sqrt{a^2+x^2}}

Pregunta 10. 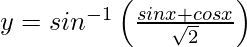y=sin^{-1}\left(\frac{sinx+cosx}{\sqrt{2}}\right) Deriva, −3π/4 < x < π/4 con respecto a x.

Solución:

Tenemos, y=sin^{-1}\left(\frac{sinx+cosx}{\sqrt{2}}\right) , −3π/4 < x < π/4

=sin^{-1}\left(sinx(\frac{1}{\sqrt{2}})+cosx(\frac{1}{\sqrt{2}})\right)

=sin^{-1}\left(sin(x+\frac{π}{4})\right)

Ahora, −3π/4 < x < π/4

=> −π/2 < (x+π/4) < π/2

Entonces, y =x+\frac{π}{4}

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(x+\frac{π}{4})

= 1 + 0

= 1

Pregunta 11. Diferenciar y=cos^{-1}\left(\frac{sinx+cosx}{\sqrt{2}}\right) , −π/4 < x < π/4 con respecto a x.

Solución:

Tenemos, y=cos^{-1}\left(\frac{sinx+cosx}{\sqrt{2}}\right) , −π/4 < x < π/4

=cos^{-1}\left(sinx(\frac{1}{\sqrt{2}})+cosx(\frac{1}{\sqrt{2}})\right)

=cos^{-1}\left(cos(x-\frac{π}{4})\right)

Ahora, −π/4 < x < π/4

=> −π/2 < (x−π/4) < 0

Entonces, y =-(x-\frac{π}{4})

=-x+\frac{π}{4}

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(-x+\frac{π}{4})

= −1 + 0

= −1

Pregunta 12. Diferenciar y=tan^{-1}\left(\frac{x}{1+\sqrt{1-x^2}}\right) , −1 < x < 1 con respecto a x.

Solución:

Tenemos, y=tan^{-1}\left(\frac{x}{1+\sqrt{1-x^2}}\right) , −1 < x < 1

Al poner x = sen θ, obtenemos,

y =tan^{-1}\left(\frac{sinθ}{1+\sqrt{1-sin^2θ}}\right)

=tan^{-1}\left(\frac{sinθ}{1+cosθ}\right)

=tan^{-1}\left(\frac{2sin\frac{θ}{2}cos\frac{θ}{2}}{2cos^2\frac{θ}{2}}\right)

=tan^{-1}\left(tan\frac{θ}{2}\right)

Ahora, −1 < x < 1

=> −1 < sen θ < 1

=> −π/2 < θ < π/2

=> −π/4 < θ/2 < π/4

Entonces, y =\frac{1}{2}sin^{-1}x

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(\frac{1}{2}sin^{-1}x)

=\frac{1}{2\sqrt{1-x^2}}

Pregunta 13. Diferenciar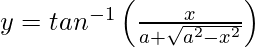y=tan^{-1}\left(\frac{x}{a+\sqrt{a^2-x^2}}\right) , −a < x < a con respecto a x.

Solución:

Tenemos, y=tan^{-1}\left(\frac{x}{a+\sqrt{a^2-x^2}}\right) , −a < x < a

Al poner x = a sen θ, obtenemos,

=tan^{-1}\left(\frac{asinθ}{a+\sqrt{a^2-a^2sin^2θ}}\right)

=tan^{-1}\left(\frac{asinθ}{a(1+cosθ)}\right)

=tan^{-1}\left(\frac{2sin\frac{θ}{2}cos\frac{θ}{2}}{2cos^2\frac{θ}{2}}\right)

=tan^{-1}\left(tan\frac{θ}{2}\right)

Ahora, −a < x < a

=> −1 < x/a < 1

=> −π/2 < θ < π/2

=> −π/4 < θ/2 < π/4

Entonces, y =\frac{1}{2}sin^{-1}(\frac{x}{a})

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(\frac{1}{2}sin^{-1}(\frac{x}{a}))

=\frac{1}{2a\sqrt{1-\frac{x^2}{a^2}}}

=\frac{a}{2a\sqrt{a^2-x^2}}

=\frac{1}{2\sqrt{a^2-x^2}}

Pregunta 14. Diferenciar 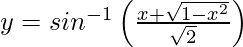y=sin^{-1}\left(\frac{x+\sqrt{1-x^2}}{\sqrt{2}}\right) , −1 < x < 1 con respecto a x.

Solución:

Tenemos, y=sin^{-1}\left(\frac{x+\sqrt{1-x^2}}{\sqrt{2}}\right) , −1 < x < 1

Al poner x = sen θ, obtenemos,

y=sin^{-1}\left(\frac{sinθ+\sqrt{1-sin^2θ}}{\sqrt{2}}\right)

=sin^{-1}\left(\frac{sinθ+cosθ}{\sqrt{2}}\right)

=sin^{-1}\left(sin(θ+\frac{π}{4})\right)

Ahora, −1 < x < 1

=> −1 < sen θ < 1

=> −π/2 < θ < π/2

=> −π/2 < (θ+π/4) < 3π/4

Entonces, y =sin^{-1}x+\frac{π}{4}

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(sin^{-1}x+\frac{π}{4})

=\frac{1}{\sqrt{1-x^2}}+0

=\frac{1}{\sqrt{1-x^2}}

Pregunta 15. Deriva 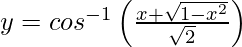y=cos^{-1}\left(\frac{x+\sqrt{1-x^2}}{\sqrt{2}}\right) , −1 < x < 1 con respecto a x.

Solución:

Tenemos, y=cos^{-1}\left(\frac{x+\sqrt{1-x^2}}{\sqrt{2}}\right) , −1 < x < 1

Al poner x = sen θ, obtenemos,

y=cos^{-1}\left(\frac{sinθ+\sqrt{1-sin^2θ}}{\sqrt{2}}\right)

=cos^{-1}\left(\frac{sinθ+cosθ}{\sqrt{2}}\right)

=cos^{-1}\left(cos(θ-\frac{π}{4})\right)

Ahora, −1 < x < 1

=> −1 < sen θ < 1

=> −π/2 < θ < π/2

=> −3π/4 < (θ−π/4) < π/4

Entonces, y =-(sin^{-1}x-\frac{π}{4})

=-sin^{-1}x+\frac{π}{4}

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(-sin^{-1}x+\frac{π}{4})

=\frac{-1}{\sqrt{1-x^2}}+0

=\frac{-1}{\sqrt{1-x^2}}

Pregunta 16. Deriva 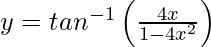y=tan^{-1}\left(\frac{4x}{1-4x^{2}}\right) , −1/2 < x < 1/2 con respecto a x.

Solución:

Tenemos, y=tan^{-1}\left(\frac{4x}{1-4x^{2}}\right) , −1/2 < x < 1/2

Al poner 2x = tan θ, obtenemos,

y=tan^{-1}\left(\frac{2tanθ}{1-tan^2θ}\right)

=tan^{-1}\left(tan2θ\right)

Ahora, −1/2 < x < 1/2

=> −1 < 2x < 1

=> −1 < bronceado θ < 1

=> −π/4 < θ < π/4

=> −π/2 < 2θ < π/2

Por lo tanto, y = 2 tan −1 (2x)

Derivando con respecto a x, obtenemos,

\frac{dy}{dx}=\frac{d}{dx}(2 tan^{−1}(2x))

=\frac{4}{\sqrt{1+(2x)^2}}

=\frac{4}{\sqrt{1+4x^2}}

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *