Pregunta 21. Encuentra dy/dx cuando 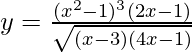 .
.
Solución:
Tenemos,
=>
=>
Al tomar el registro de ambos lados, obtenemos,
=>
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 22. Halle dy/dx cuando 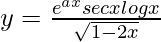 .
.
Solución:
Tenemos,
=>
=>
Al tomar el registro de ambos lados, obtenemos,
=>
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 23. Encuentra dy/dx cuando y = e 3x sen 4x 2 x .
Solución:
Tenemos
=> y = mi 3x sen 4x 2 x .
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (e 3x sen 4x 2 x )
=> log y = log e 3x + log (sen 4x) + log 2 x
=> log y = 3x log e + log (sen 4x) + x log 2
=> log y = 3x + log (sen 4x) + x log 2
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 24. Encuentra dy/dx cuando y = sen x sen 2x sen 3x sen 4x.
Solución:
Tenemos,
=> y = sen x sen 2x sen 3x sen 4x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (sen x sen 2x sen 3x sen 4x)
=> log y = log sen x + log sen 2x + log sen 3x + log sen 4x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
= cotx + 2cot2x + 3cot3x + 4cot4x
=>
= y(cotx + 2cot2x + 3cot3x + 4cot4x)
=>
= (senxsen2x sin3xsen4x)(cotx + 2cot2x + 3cot3x + 4cot4x)
Pregunta 25. Encuentra dy/dx cuando y = x sen x + (sen x) x .
Solución:
Tenemos,
=> y = x sen x + (sen x) x .
Sean u = x sen x y v = (sen x) x . Por lo tanto, y = u + v.
Ahora, u = x sen x
Al tomar el registro de ambos lados, obtenemos,
=> log u = log x sen x
=> log u = sen x log x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Además, v = (sen x) x
Al tomar el registro de ambos lados, obtenemos,
=> log v = log (sen x) x
=> log v = x log sen x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Ahora tenemos, y = u + v.
=>
=>
Pregunta 26. Encuentra dy/dx cuando y = (sen x) cos x + (cos x) sen x .
Solución:
Tenemos,
=> y = (sen x) cos x + (cos x) sen x
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
= (senx) cosx [cosxcotx – sinxlog(senx)] + (cosx) sinx [-tanxsenx + cosxlog(cosx)]
=>
= (senx) cosx [cosxcotx – sinxlog(senx)] + (cosx) senx [cosxlog(cosx) – tanxsenx]
Pregunta 27. Encuentra dy/dx cuando y = (tan x) cot x + (cot x) tan x .
Solución:
Tenemos,
=> y = (bronceado x) cuna x + (cot x) bronceado x
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
= (tanx) cotx [cosec 2 x – log(tanx)(cosec 2 x)] + (cotx) tanx [-sec 2 x + log(cotx)(sec 2 x)]
=>
= (tanx) cotx [cosec 2 x – cosec 2 xlog(tanx)] + (cotx) tanx [sec 2 xlog(cotx) – sec 2 x]
Pregunta 28. Encuentra dy/dx cuando y = (sin x) x + sin −1 √x.
Solución:
Tenemos,
=> y = (sen x) x + sen −1 √x
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Pregunta 29. Encuentra dy/dx cuando
(i) y = x cos x + (sen x) tan x
Solución:
Tenemos,
=> y = x cos x + (sen x) tan x
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
(ii) y = x x + (sen x) x
Solución:
Tenemos,
=> y = x x + (sen x) x
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Pregunta 30. Encuentra dy/dx cuando y = (tan x) log x + cos 2 (π/4).
Solución:
Tenemos,
=> y = (tan x) log x + cos 2 (π/4)
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Pregunta 31. Encuentra dy/dx cuando 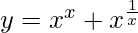 .
.
Solución:
Tenemos,
=>
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 32. Encuentra dy/dx cuando y = (log x) x + x logx .
Solución:
Tenemos,
=> y = (log x) x + x logx
Sean u = (log x) x y v = x logx . Por lo tanto, y = u + v.
Ahora, u = (log x) x
Al tomar el registro de ambos lados, obtenemos,
=> registro u = registro (registro x) x
=> log u = x log (log x)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
Además, v = x logx
Al tomar el registro de ambos lados, obtenemos,
=> log v = log x logx
=> registro v = registro x (registro x)
=> log v = (log x) 2
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Ahora, y = u + v
=>
=>
Pregunta 33. Si x 13 y 7 = (x+y) 20 , prueba que 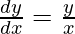 .
.
Solución:
Tenemos,
=> x 13 y 7 = (x+y) 20
Al tomar el registro de ambos lados, obtenemos,
=> logaritmo x 13 y 7 = logaritmo (x+y) 20
=> log x 13 + log y 7 = log (x+y) 20
=> 13 log x + 7 log y = 20 log (x+y)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 34. Si x 16 y 9 = (x 2 + y) 17 , prueba que 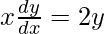 .
.
Solución:
Tenemos,
=> x 16 y 9 = (x 2 + y) 17
Al tomar el registro de ambos lados, obtenemos,
=> logaritmo x 16 y 9 = logaritmo (x 2 + y) 17
=> logaritmo x 16 + logaritmo y 9 = logaritmo (x 2 +y) 17
=> 16 log x + 9 log y = 17 log (x 2 + y)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 35. Si y = sen x x , demuestre que 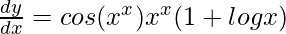 .
.
Solución:
Tenemos,
=> y = sen x x
Sea u = x x . Ahora y = sen u.
Al tomar el registro de ambos lados, obtenemos,
=> registro u = registro x x
=> log u = x log x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Ahora, y = sen u
=>
=>
=>
Por lo tanto probado.
Pregunta 36. Si x x + y x = 1, demuestre que 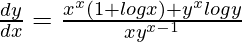 .
.
Solución:
Tenemos,
=> x x + y x = 1
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 37. Si x y × y x = 1, prueba que 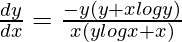 .
.
Solución:
Tenemos,
=> x y × y x = 1
Al tomar el registro de ambos lados, obtenemos,
=> logaritmo (x y × y x ) = logaritmo 1
=> log x y + log y x = log 1
=> y log x + x log y = log 1
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 38. Si x y + y x = (x+y) x+y , encuentra dy/dx.
Solución:
Tenemos,
=> x y + y x = (x+y) x+y
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 39. Si x m y n = 1, demuestre que  .
.
Solución:
Tenemos,
=> x metro y norte = 1
Al tomar el registro de ambos lados, obtenemos,
=> logaritmo (x m y n )= logaritmo 1
=> log x m + log y n = log 1
=> m log x + n log y = log 1
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 40. Si y x = e y−x , demuestre que 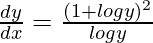 .
.
Solución:
Tenemos,
=> y x = e y−x
Al tomar el registro de ambos lados, obtenemos,
=> log y x = log e y−x
=> x log y = (y − x) log e
=> x log y = y − x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
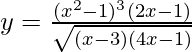
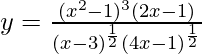
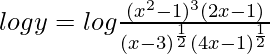
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{(x^2-1)^3(2x-1)}{\sqrt{(x-3)(4x-1)}}\left[\frac{6x}{x^2-1}+\frac{2}{2x-1}-\frac{1}{2(x-3)}-\frac{2}{4x-1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2009aaa4bafcb70ef29ffd7f09289dc6_l3.png)
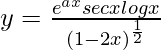
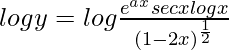
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{cosxlog(sin x)})[cosx(\frac{1}{sinx})cosx+log(sinx)(-sinx)] + (e^{sinxlog(cos x)})[sinx(\frac{1}{cosx})(-sinx)+log(cosx)(cosx)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-381af831a4aebeb66d66c1bb943808c2_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{cotxlog(tanx)})[cotx(\frac{1}{tanx})(sec^2x)+log(tanx)(-cosec^2x)] + (e^{tanxlog(cot x)})[tanx(\frac{1}{cotx})(-cosec^2x)+log(cotx)(sec^2x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-700347737176ab2e9b9f7c2431ebd2fe_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(tanx)^{cotx}[cot^2x(sec^2x)-log(tanx)(cosec^2x)] + (cotx)^{tanx}[tan^2x(-cosec^2x)+log(cotx)(sec^2x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4169c6a5a4d3f70c0663646b393bd270_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{cosxlogx})[cosx(\frac{1}{x})+logx(-sinx)] + (e^{tanxlog(sinx)})[tanx(\frac{1}{sinx})(cosx)+log(sinx)sec^2x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1922a26dfd2bac900945c5e03ae6c9ac_l3.png)
![Rendered by QuickLaTeX.com (e^{ylogx})[y(\frac{1}{x})+logx(\frac{dy}{dx})] + (e^{xlogy})[x(\frac{1}{y})(\frac{dy}{dx})+logy]=(e^{(x+y)log(x+y)})[(x+y)(\frac{1}{x+y})(1+\frac{dy}{dx})+log(x+y)(1+\frac{dy}{dx})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bc3faa98d841e3e35271fb6ea78c02d7_l3.png)
![Rendered by QuickLaTeX.com e^{ylogx}[\frac{y}{x}+logx(\frac{dy}{dx})] + (e^{xlogy})[(\frac{x}{y})(\frac{dy}{dx})+logy]=(e^{(x+y)log(x+y)})[1+\frac{dy}{dx}+log(x+y)(1+\frac{dy}{dx})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c055c357eceda950cfaa2dc219d98c95_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}[x^ylogx+xy^{x-1}-(x+y)^{x+y}(1+log(x+y))]=(x+y)^{x+y}(1+log(x+y))-yx^{y-1}-y^xlogy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-903e4408e5dd206249232b7014c062eb_l3.png)