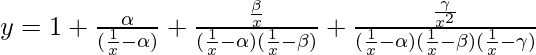Pregunta 41. Si (sen x) y = (cos y) x , demuestre que 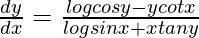 .
.
Solución:
Tenemos,
=> (sen x) y = (cos y) x
Al tomar el registro de ambos lados, obtenemos,
=> log (sen x) y = log (cos y) x
=> y log (sen x) = x log (cos y)
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 42. Si (cos x) y = (tan y) x , prueba que \frac{dy}{dx}=\frac{log tany+ytanx}{logcosx-xsecycosecy} .
Solución:
Tenemos, (cos x) y = (tan y) x
Al tomar el registro de ambos lados, obtenemos,
=> log (cos x) y = log (tan y) x
=> y log (cos x) = x log (tan y)
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 43. Si e x + e y = e x+y , demuestre que 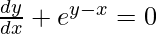 .
.
Solución:
Tenemos,
=> e x + e y = e x+y
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 44. Si e y = y x , demuestre que 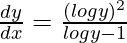 .
.
Solución:
Tenemos,
=> e y = y x
Al tomar el registro de ambos lados, obtenemos,
=> log e y = log y x
=> y log e = x log y
=> y = x log y
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 45. Si e x+y − x = 0, demuestre que 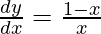 .
.
Solución:
Tenemos,
=> e x+y − x = 0
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
Ahora sabemos que e x+y − x = 0
=> e x+y = x
Entonces, obtenemos,
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 46. Si y = x sen (a+y), demuestre que 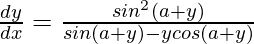 .
.
Solución:
Tenemos,
=> y = x sen (a+y)
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Ahora sabemos, y = x sen (a+y)
=>
Entonces, obtenemos,
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 47. Si x sen (a+y) + sen a cos (a+y) = 0, demuestre que 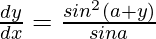 .
.
Solución:
Tenemos,
=> x sen (a+y) + sen a cos (a+y) = 0
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Ahora sabemos, x sen (a+y) + sen a cos (a+y) = 0
=>
Entonces, obtenemos,
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 48. Si (sen x) y = x + y, demuestre que 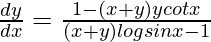 .
.
Solución:
Tenemos,
=> (sen x) y = x + y
Al tomar el registro de ambos lados, obtenemos,
=> log (sen x) y = log (x + y)
=> y logaritmo sen x = logaritmo (x + y)
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 49. Si xy log (x+y) = 1, demuestre que 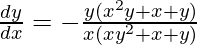 .
.
Solución:
Tenemos,
=> logaritmo xy (x+y) = 1
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
Ahora sabemos que xy log (x+y) = 1.
=>
Entonces, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 50. Si y = x sen y, demuestre que 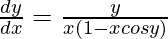 .
.
Solución:
Tenemos,
=> y = x sen y
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Ahora sabemos que y = x sen y
=>
Entonces, obtenemos,
=>
=>
=>
Por lo tanto probado.
Pregunta 51. Halla la derivada de la función f(x) dada por,
f(x) = (1+x) (1+x 2 ) (1+x 4 ) (1+x 8 ) y por lo tanto encuentre f'(1).
Solución:
Aquí nos dan,
=> f(x) = (1+x) (1+x 2 ) (1+x 4 ) (1+x 8 )
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
Ahora, el valor de f'(x) en 1 es,
=> f'(1) = (1 + 1) (1 + 1) (1 + 1) (8) + (1 + 1) (1 + 1) (1 + 1) (4) + (1 + 1 ) (1 + 1) (1 + 1) (2) + (1 + 1) (1 + 1) (1 + 1) (1)
=> f'(1) = (2) (2) (2) (8) + (2) (2) (2) (4) + (2) (2) (2) (2) + (2) (2) (2) (1)
=> f'(1) = 64 + 32 + 16 + 8
=> f'(1) = 120
Por tanto, el valor de f'(1) es 120.
Pregunta 52. Si 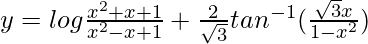 , encuentra
, encuentra 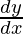 .
.
Solución:
Se nos da,
=>
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
Pregunta 53. Si y = (sen x − cos x) sen x−cos x , π/4 < x < 3π/4, encuentre 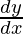 .
.
Solución:
Tenemos,
=> y = (sen x − cos x) sen x−cos x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (sen x − cos x) sen x−cos x
=> log y = (sen x − cos x) log (sen x−cos x)
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
= (1)(cosx + senx) + (cosx + senx)log (sen x − cos x)
=>
= cosx + senx + (cosx + senx)log (sen x − cos x)
=>
= (cosx + senx)(1 + log (sen x − cos x))
=>
= y(cosx + senx)(1 + log (sen x − cos x))
=>
= (senx – cosx) senx-cosx (cosx + senx)(1 + log (sen x − cos x))
Pregunta 54. Halla dy/dx de la función xy = e x-y .
Solución:
Tenemos,
=> xy = e x-y
Al tomar el registro de ambos lados, obtenemos,
=> log xy = log e x-y
=> log x + log y = (x − y) log e
=> log x + log y = x − y
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 55. Encuentra dy/dx de la función y x + x y + x x = a b .
Solución:
Tenemos,
=> y x + x y + x x = un segundo
=>
=>
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
Pregunta 56. Si (cos x) y = (cos y) x , encuentra dy/dx.
Solución:
Tenemos,
=> (cos x) y = (cos y) x
Al tomar el registro de ambos lados, obtenemos,
=> log (cos x) y = log (cos y) x
=> y logaritmo (cos x) = x logaritmo (cos y)
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 57. Si cos y = x cos (a+y), donde cos a ≠ ±1, demuestre que 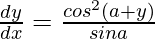 .
.
Solución:
Tenemos,
=> cos y = x cos (a+y)
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 58. Si 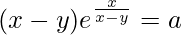 , demuestre que
, demuestre que 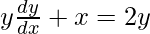 .
.
Solución:
Tenemos,
=>
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 59. Si 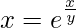 , demuestre que
, demuestre que 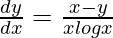 .
.
Solución:
Tenemos,
=>
Al tomar el registro de ambos lados, obtenemos,
=> registro x = registro
=>
=>
=>
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
Sabemos,
=>
Entonces, obtenemos,
=>
=>
=>
=>
=>
Por lo tanto probado.
Pregunta 60. Si 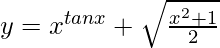 , encuentra dy/dx.
, encuentra dy/dx.
Solución:
Tenemos,
=>
=>
=>
Al derivar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Pregunta 61. Si 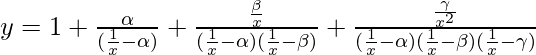 , encuentra dy/dx.
, encuentra dy/dx.
Solución:
Se nos da,
=>
Ahora sabemos,
si
entonces,
En la expresión dada, tenemos 1/x en lugar de x.
Entonces, usando el teorema anterior, obtenemos,
=>
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
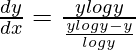
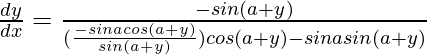
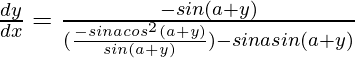
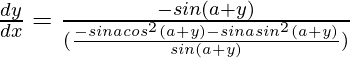
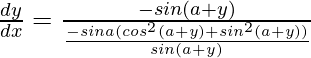
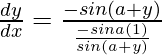
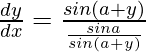
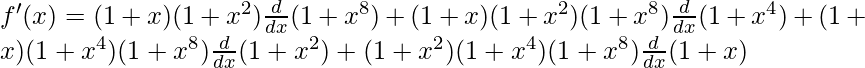
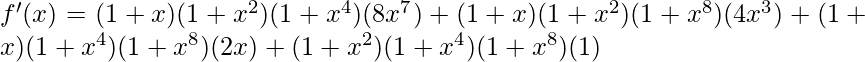
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{1}{\frac{x^2+x+1}{x^2-x+1}}\frac{d}{dx}(\frac{x^2+x+1}{x^2-x+1})+\frac{2}{\sqrt{3}}\left[\frac{1}{1+(\frac{\sqrt{3}x}{1-x^2})^2}\right]\frac{d}{dx}(\frac{\sqrt{3}x}{1-x^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46f01c999ec46901888fcc1bac445c0d_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{x^2-x+1}{x^2+x+1}\left[\frac{(x^2-x+1)(2x+1)-(x^2+x+1)(2x-1)}{(x^2-x+1)^2}\right]+\frac{2}{\sqrt{3}}\left[\frac{1}{1+\frac{3x^2}{(1-x^2)^2}}\right]\left[\frac{(1-x^2)(\sqrt{3})-\sqrt{3}x(-2x)}{(1-x^2)^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d41b09de98871a2ef0f4e80bb82362fd_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{1}{x^2+x+1}\left[\frac{2x^3+x^2-2x^2-x+2x+1-2x^3-2x^2-2x+x^2+x+1}{x^2-x+1}\right]+\frac{2}{\sqrt{3}}\left[\frac{1}{\frac{(1-x^2)^2+3x^2}{(1-x^2)^2}}\right]\left[\frac{\sqrt{3}-\sqrt{3}x^2+2\sqrt{3}x^2}{(1-x^2)^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3d5f2ee27b32b20dbcf69357aec004a2_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{-2x^2+2}{x^4+2x^2+1-x^2}+\frac{2}{\sqrt{3}}\left[\frac{1}{\frac{1+x^4-2x^2+3x^2}{(1-x^2)^2}}\right]\left[\frac{\sqrt{3}+\sqrt{3}x^2}{(1-x^2)^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6426b89bf95e614846f3bf523c1e41ae_l3.png)
![Rendered by QuickLaTeX.com (x-y)\left[(e^{\frac{x}{x-y}})[\frac{(x-y)-x(1-\frac{dy}{dx})}{(x-y)^2}]\right]+e^{\frac{x}{x-y}}(1-\frac{dy}{dx})=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fafbadb72d57c59daaf76c2b69c135a5_l3.png)