Pregunta 1. Diferenciar y = x 1/x con respecto a x.
Solución:
Tenemos,
=> y = x1 /x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log x 1/x
=> log y = (1/x) (log x)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
Pregunta 2. Diferenciar y = x sen x con respecto a x.
Solución:
Tenemos,
=> y = x sen x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log x sen x
=> log y = sen x log x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 3. Diferenciar y = (1 + cos x) x con respecto a x.
Solución:
Tenemos,
=> y = (1 + cos x) x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (1 + cos x) x
=> log y = x log (1 + cos x)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
Pregunta 4. Diferenciar 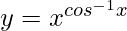 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=>
Al tomar el registro de ambos lados, obtenemos,
=> registro y = registro
=> log y = cos −1 x log x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 5. Diferenciar y = (log x) x con respecto a x.
Solución:
Tenemos,
=> y = (log x) x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (log x) x
=> log y = x log (log x)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 6. Derive y = (log x) cos x con respecto a x.
Solución:
Tenemos,
=> y = (log x) cos x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (log x) cos x
=> log y = cos x log (log x)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 7. Diferenciar y = (sen x) cos x con respecto a x.
Solución:
Tenemos,
=> y = (sen x) cos x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (sen x) cos x
=> log y = cos x log (sen x)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
Pregunta 8. Diferenciar y = e x log x con respecto a x.
Solución:
Tenemos,
=> y=e x log x
=> y =
=> y = x x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log x x
=> log y = x log x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 9. Diferenciar y = (sen x) log x con respecto a x.
Solución:
Tenemos,
=> y = (sen x) log x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (sen x) log x
=> log y = log x log (sen x)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 10. Diferenciar y = 10 log sen x con respecto a x.
Solución:
Tenemos,
=> y = 10 log sen x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log 10 log sen x
=> log y = log (sen x) log 10
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
Pregunta 11. Diferenciar y = (log x) log x con respecto a x.
Solución:
Tenemos,
=> y = (registro x) registro x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (log x) log x
=> log y = log x log (log x)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
Pregunta 12. Diferenciar 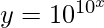 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=>
Al tomar el registro de ambos lados, obtenemos,
=> registro y = registro
=> log y = 10 x log 10
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
Pregunta 13. Diferenciar y = sen x x con respecto a x.
Solución:
Tenemos,
=> y = sen x x
=> sen −1 y = x x
Al tomar el registro de ambos lados, obtenemos,
=> log (sen −1 y) = log x x
=> log (sen −1 y) = x log x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
=>
=>
=>
Pregunta 14. Diferenciar y = (sin −1 x) x con respecto a x.
Solución:
Tenemos,
=> y = (sen −1 x) x
Al tomar el registro de ambos lados, obtenemos,
=> log y = (sen −1 x) x
=> log y = x log (sen −1 x)
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 15. Diferenciar 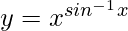 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=>
Al tomar el registro de ambos lados, obtenemos,
=> registro y = registro
=> log y = sen −1 x log x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 16. Diferenciar 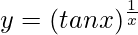 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=>
Al tomar el registro de ambos lados, obtenemos,
=> registro y = registro
=> log y =
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 17. Diferenciar 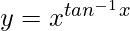 con respecto a x.
con respecto a x.
Solución:
Tenemos,
=>
Al tomar el registro de ambos lados, obtenemos,
=> registro y = registro
=> log y = tan −1 x log x
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
Pregunta 18. Diferencie lo siguiente con respecto a x.
(i) y = x x √x
Solución:
Tenemos,
=> y = x x √x
Al tomar el registro de ambos lados, obtenemos,
=> log y = log (x x √x)
=> log y = log x x + log √x
=> log y = x log x +
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
(ii) 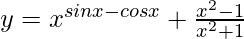
Solución:
Tenemos,
=>
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
(iii) 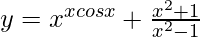
Solución:
Tenemos,
=>
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
(iv) y = (x cos x) x + (x sen x) 1/x
Solución:
Tenemos,
=> y=(x cos x) x + (x sen x) 1/x
=>
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
(v) 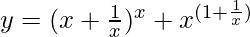
Solución:
Tenemos,
=>
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
=>
(vi) y = e sen x + (tan x) x
Solución:
Tenemos,
=> y = e sen x + (tan x) x
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
(vii) y = (cos x) x + (sen x) 1/x
Solución:
Tenemos,
=> y = (cos x) x + (sen x) 1/x
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
( viii) 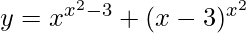 , para x > 3
, para x > 3
Solución:
Tenemos,
=>
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
Pregunta 19. Encuentra dy/dx cuando y = e x + 10 x + x x .
Solución:
Tenemos,
=> y = e x + 10 x + x x
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Pregunta 20. Encuentra dy/dx cuando y = x n + n x + x x + n n .
Solución:
Tenemos,
=> y = x norte + norte x + x x + norte norte
=>
=>
Al diferenciar ambos lados con respecto a x, obtenemos,
=>
=>
=>
=>
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{(sinx-cosx)logx})[(sinx-cosx)\frac{1}{x}+logx(cosx+sinx)]+\frac{(x^2+1)(2x)-(x^2-1)(2x)}{(x^2+1)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-223abb9a2f9b45a3be317e0aa2f276b3_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{x(logx+logcosx)})[x(\frac{1}{x}+(\frac{1}{cosx})(-sinx))+log(xcosx)(1)]+ (e^{\frac{1}{x}(logx+logsin x)})[\frac{1}{x}(\frac{1}{x}+(\frac{1}{sinx})(cosx))+log(xsinx)(\frac{-1}{x^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-44ceed2b2c359e2817041dccfa8aaa43_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{x(logx+logcosx)})[1-xtanx+log(xcosx)]+ (e^{\frac{1}{x}(logx+logsin x)})[\frac{1}{x^2}+\frac{1}{xcotx}-\frac{log(xsinx)}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87bce6c0b324a1d4627de24314359085_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{x(logx+logcosx)})[1-xtanx+log(xcosx)]+ (e^{\frac{1}{x}(logx+logsin x)})[\frac{1-log(xsinx)+xcotx}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8643e9cee8dd0ea097e2a78d6ed2132f_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xlog(x+\frac{1}{x})})[x(\frac{1}{x+\frac{1}{x}})(1-\frac{1}{x^2})+log(x+\frac{1}{x})]+(e^{(1+\frac{1}{x})logx})[(1+\frac{1}{x})(\frac{1}{x})+logx(\frac{-1}{x^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d4f426b1ffa47c5bb9e14bd6ce00fa4_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xlog(x+\frac{1}{x})})[(\frac{x-\frac{1}{x}}{x+\frac{1}{x}})+log(x+\frac{1}{x})]+(e^{(1+\frac{1}{x})logx})[\frac{1}{x}+\frac{1}{x^2}-logx(\frac{1}{x^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-202c59a9a42e1ce050b0c9185420d964_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{xlog(cos x)})[x(\frac{1}{cosx})(-sinx)+log(cosx)] + (e^{\frac{1}{x}log(sin x)})[\frac{1}{x}(\frac{1}{sinx}(cosx))+log(sinx)(-\frac{1}{x^2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab41de374063ad33774b84d648fa4e5e_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dx}=(e^{(x^2-3)logx})[(x^2-3)(\frac{1}{x})+logx(2x)]+(e^{x^2log(x-3)})[x^2(\frac{1}{x-3})+log(x-3)(2x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91b6f8b9b455b02faaaa800c46a3d1de_l3.png)