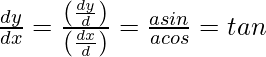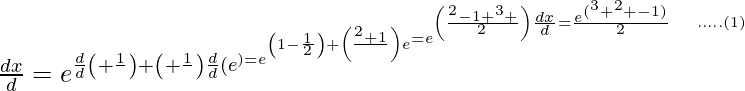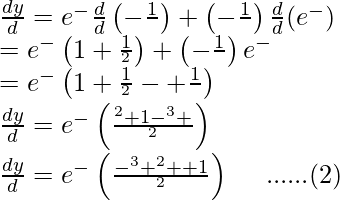Pregunta 1. Encuentra 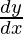 , cuando: x = en 2 y y = 2 en
, cuando: x = en 2 y y = 2 en
Solución:
Dado que x = en 2 , y = 2 en
Asi que,
Por lo tanto,
Pregunta 2. Encuentra 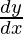 , cuando: x = a(θ + sinθ) y y = a(1 – cosθ)
, cuando: x = a(θ + sinθ) y y = a(1 – cosθ)
Solución:
Aquí,
x = a(θ + senθ)
Derivando con respecto a θ,
y,
y = a(1 – cosθ)
Derivarlo con respecto a θ,
Usando la ecuación (1) y (2),
Pregunta 3. Encuentra 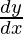 , cuando: x = acosθ y y = bsinθ
, cuando: x = acosθ y y = bsinθ
Solución:
Entonces x = acosθ y y = bsinθ
Después,
Por lo tanto,
Pregunta 4. Encuentra 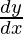 , cuando: x = a e Θ (sinθ -cosθ), y = ae Θ (sinθ +cosθ)
, cuando: x = a e Θ (sinθ -cosθ), y = ae Θ (sinθ +cosθ)
Solución:
Aquí,
x = ae Θ (senθ – cosθ)
Derivando con respecto a θ,
Y,
y = ae Θ (senθ+cosθ)
Derivando con respecto a θ
Dividiendo la ecuación (2) por la ecuación (1)
Pregunta 5. Halla 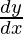 , cuando: x = bsen 2 θ y y = acos 2 θ
, cuando: x = bsen 2 θ y y = acos 2 θ
Solución:
Aquí,
x = bsen 2 θ y y = acos 2 θ
Después,
Pregunta 6. Encuentra 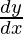 , cuando: x = a(1 – cos θ) y y = a(θ +senθ) en θ =
, cuando: x = a(1 – cos θ) y y = a(θ +senθ) en θ =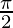
Solución:
Aquí,
x = a(1 – cosθ) y y = a(θ + senθ)
Después,
Por lo tanto,
Pregunta 7. Encuentra 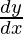 , cuando:
, cuando: 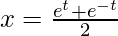 y
y
Solución:
Aquí,
Derivarlo con respecto a t,
y,
Derivando con respecto a t,
Dividiendo la ecuación (2) y (1)
Pregunta 8. Encuentra 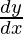 , cuando:
, cuando: 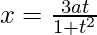 y
y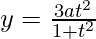
Solución:
Aquí,
Derivando con respecto a t usando la regla del cociente,
y,
Derivando con respecto a t usando la regla del cociente,
Dividiendo la ecuación (2) por (1)
Pregunta 9. Si x e y están conectados paramétricamente por la ecuación, sin eliminar el parámetro, encuentre 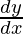 cuando: x = a(cosθ +θsinθ), y = a(sinθ -θcosθ)
cuando: x = a(cosθ +θsinθ), y = a(sinθ -θcosθ)
Solución:
Las ecuaciones dadas son
x = a(cosθ +θ sinθ) y y = a(sinθ -θcosθ)
Después,
= a[-sinθ + θcosθ + sinθ] = aθcosθ
= a[cosθ +θsenθ -cosθ]
= aθsenθ
Por lo tanto,
Pregunta 10. Encuentra 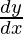 , cuando:
, cuando: 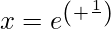 y
y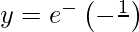
Solución:
Aquí,
Derivando con respecto a θ usando la regla del producto,
y,
Derivando con respecto a θ usando la regla del producto y la regla de la string
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
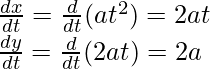
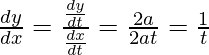

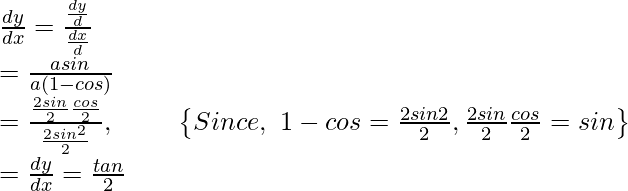
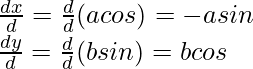
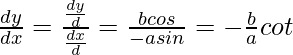
![Rendered by QuickLaTeX.com \frac{dx}{dθ}=a[e^θ\frac{d}{dθ}(sinθ-cosθ)+(sinθ-cosθ)\frac{d}{dθ}(e^θ)]\\ =a[e^θ(cosθ+sinθ)+(sinθ-cosθ)e^θ]\\ \frac{dx}{dθ}=a[2e^θsinθ]\ \ \ \ \ \ .......(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2ae44003272bf3428cebf6561cbb74c4_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dθ}=a[e^θ\frac{d}{dθ}(sinθ+cosθ)+(sinθ+cosθ)\frac{d}{dθ}(e^θ)]\\ =a[e^θ(cosθ-sinθ)+(sinθ+cosθ)e^θ]\\ \frac{dx}{dθ}=a[2e^θcosθ]\ \ \ \ \ \ .......(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-322bbedc6e2f747634da1bbf9987f88e_l3.png)
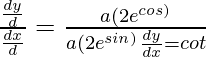
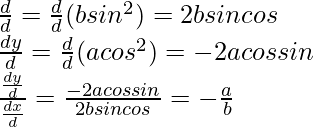
![Rendered by QuickLaTeX.com \frac{dx}{dθ}=\frac{d}{dθ}[a(1-cosθ)]=asinθ\\ \frac{dy}{dθ}=\frac{d}{dθ}[a(θ +sinθ)]=a(1+cosθ)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7a39d173d5f8bc38c6edaad0629b8e58_l3.png)
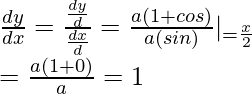
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\frac{1}{2}\left[\frac{d}{dt}(e^t)+\frac{d}{dt}(e^{-t})\right]\\ =\frac{1}{2}\left[e^t+e^{-t}\frac{d}{dt}(e^{-t})\right]\\ \frac{dx}{dt}=\frac{1}{2}(e^t-e^{-t})=y\ \ \ ......(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f82afd089cd07a5a4bb21127dd523341_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\frac{1}{2}\left[\frac{d}{dt}(e^t)-\frac{d}{dt}(e^{-t})\right]\\ =\frac{1}{2}\left[e^t-e^{-t}\frac{d}{dt}(e^{-t})\right]\\ \frac{dx}{dt}=\frac{1}{2}(e^t+e^{-t})=x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0374781882627f150ffd3dce4d85518_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\frac{1}{2}\left[\frac{d}{dt}(e^t)-\frac{d}{dt}(e^{-t})\right]\\ =\frac{1}{2}\left[e^t-e^{-t}\frac{d}{dt}(e^{-t})\right]\\ \frac{dx}{dt}=\frac{1}{2}(e^t+e^{-t})=x\ \ \ \ .....(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aaef7944d5445fbd5afcc836606061d5_l3.png)
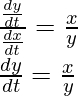
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(3at)-3at\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(3a)-3at(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{3a+3at^2-6at^2}{(1+t^2)^2}\right]\\ =\left[\frac{3a-3at^2}{(1-t^2)^2}\right]\\ \frac{dx}{dt}=\frac{3a(1-t^2)}{(1+t^2)^2}\ \ \ \ ....(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-66b0fcdb192f11a038cebecc2448593d_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(3at^2)-3at^2\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(6at)-(3at^2)(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{6at+6at^3-6at^3}{(1+t^2)^2}\right]\\ \frac{dy}{dt}=\frac{6at}{(1+t^2)^2}\ \ \ \ ....(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-193c0a0b50b7cc8a3f19caffc740c1f9_l3.png)
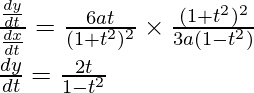
![Rendered by QuickLaTeX.com \frac{dx}{dθ}=a\left[\frac{d}{dθ}cosθ +\frac{d}{dθ}(θ sinθ)\right]\\ =a\left[-sinθ +θ \frac{d}{dθ}(sinθ)+sinθ \frac{d}{dθ}(θ)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ba02a50e8787421b2adfe6e2b974fb2_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dθ}=a\left[\frac{d}{dθ}sinθ +\frac{d}{dθ}(θ cosθ)\right]\\ =a\left[cosθ -\{θ \frac{d}{dθ}(cosθ)+cosθ \frac{d}{dθ}(θ)\}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bae259f6ef8efa5e670376cde4041048_l3.png)