Pregunta 9: Usando diferenciales, encuentre los valores aproximados de lo siguiente:
(xiv) 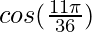
Solución:
Considerando la función como
y = f(x) = cos x
Tomando x = π/3, y
x+△x = 11π/36
△x = 11π/36-π/3 = -π/36
y = cos x
= coseno (π/3) = 0,5
= – sen x
= – sen (π/3) = -0.86603
△y = dy =
dx
△y = (-0.86603) (-π/36)
△y = 0.0756
Por lo tanto,
= 0,5+0,0756 = 0,5755
(xvi) 
Solución:
Considerando la función como
y = f(x) =
Tomando x = 81, y
x+△x = 80
△x = 80-81 = -1
△y = dy =
dx
△y =
△x
△y =
(-1) =
= -0.009259
Por eso,
= y+△y = 3 + (-0.009259) = 2.99074
(xi) 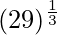
Solución:
Considerando la función como
y = f(x) =
Tomando x = 27, y
x+△x = 29
△x = 29-27 = 2
△y = dy =
dx
△y =
△x
△y =
(2) = 0.074
Por eso,
= y+△y = 3+0.074 = 3.074
(xviii) 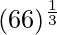
Solución:
Considerando la función como
y = f(x) =
Tomando x = 64, y
x+△x = 66
△x = 66-64 = 2
△y = dy =
dx
△y =
△x
△y =
(2) = 0.042
Por eso,
= y+△y = 4+0.042 = 4.042
(xviii) 
Solución:
Considerando la función como
y = f(x) =
Tomando x = 25, y
x+△x = 26
△x = 26-25 = 1
△y = dy =
dx
△y =
△x
△y =
(1) = 0.1
Por eso,
= y+△y = 5 + 0.1 = 5.1
(xix) 
Solución:
Considerando la función como
y = f(x) =
Tomando x = 36, y
x+△x = 37
△x = 37-36 = 1
△y = dy =
dx
△y =
△x
△y =
(1) = 0.0833
Por eso,
= y+△y = 6 + 0,0833 = 6,0833
(xx) 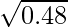
Solución:
Considerando la función como
y = f(x) =
Tomando x = 0.49, y
x+△x = 0.48
△x = 0,48-0,49 = -0,01
△y = dy =
dx
△y =
△x
△y =
(-0.01) = -0.007143
Por eso,
= y+△y = 0,7 + (-0,007143) = 0,693
(xx) 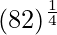
Solución:
Considerando la función como
y = f(x) =
Tomando x = 81, y
x+△x = 82
△x = 82-81 = 1
△y = dy =
dx
△y =
△x
△y =
= 0.009259
Por eso,
= y+△y = 3 + 0.009259 = 3.009259
(xii) 
Solución:
Considerando la función como
y = f(x) =
Tomando x = 16/81, y
x+△x = 17/81
△x = 17/81-16/81 = 1/81
△y = dy =
dx
△y =
△x
△y =
= 0.01042
Por eso,
= y+△y = 2/3 + 0,01042 = 0,6771
(xiii) 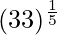
Solución:
Considerando la función como
y = f(x) =
Tomando x = 32, y
x+△x = 33
△x = 33-32 = 1
△y = dy =
dx
△y =
△x
△y =
= 0.0125
Por eso,
= y+△y = 2 + 0.0125 = 2.0125
(xiv) 
Solución:
Considerando la función como
y = f(x) =
Tomando x = 36, y
x+△x = 36,6
△x = 36,6-36 = 0,6
△y = dy =
dx
△y =
△x
△y =
(0,6) = 0,05
Por eso,
= y+△y = 6 + 0,05 = 6,05
(xv) 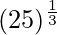
Solución:
Considerando la función como
y = f(x) =
Tomando x = 27, y
x+△x = 25
△x = 25-27 = -2
△y = dy =
dx
△y =
△x
△y =
(-2) = -0.07407
Por eso,
= y+△y = 3+(-0.07407) = 2.9259
(xxi) 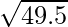
Solución:
Considerando la función como
y = f(x) =
Tomando x = 49, y
x+△x = 49.5
△x = 49,5-49 = 0,5
△y = dy =
dx
△y =
△x
△y =
(0.5) = 0.0357
Por eso,
= y+△y = 7 + 0,0357 = 7,0357
Pregunta 10: Encuentra el valor apropiado de f(2.01), donde f(x) = 4x 2 +5x+2
Solución:
Considerando la función como
y = f(x) = 4x 2 +5x+2
Tomando x = 2, y
x+△x = 2.01
△x = 2,01-2 = 0,01
y = 4x 2 +5x+2
= 4(2) 2 +5(2)+2 = 28
= 8x+5
= 8(2)+5 = 21
△y = dy =
dx
△y = (21) △x
△y = (21) (0,01) = 0,21
Por eso,
f(2.01) = y+△y = 28 + 0.21 = 28.21
Pregunta 11: Encuentra el valor apropiado de f(5.001), donde f(x) = x 3 -7x 2 +15
Solución:
Considerando la función como
y = f(x) = x 3 -7x 2 +15
Tomando x = 5, y
x+△x = 5.001
△x =5.001-5 = 0.001
y = x 3 -7x 2 +15
= (5) 3 -7(5) 2 +15 = -35
= 3x 2 -14x
= 3(5) 2 -14(5) = 5
△y = dy =
dx
△y = (5) △x
△y = (5) (0.001) = 0.005
Por eso,
f(5.001) = y+△y = -35 + 0.005 = -34.995
Pregunta 12: Encuentra el valor apropiado de log 10 1005, dado que log 10 e=0.4343
Solución:
Considerando la función como
y = f(x) = registro 10 x
Tomando x = 1000, y
x+△x = 1005
△x =1005-1000 = 5
y = registro 10 x =
= registro 10 1000 = 3
= 0.0004343
△y = dy =
dx
△y = (0.0004343) △x
△y = (0.0004343) (5) = 0.0021715
Por lo tanto, log 10 1005 = y+△y = 3 + 0,0021715 = 3,0021715
Pregunta 13: Si el radio de una esfera mide 9 cm con un error de 0,03 m, encuentre el error aproximado al calcular su área de superficie.
Solución:
Según la condición dada,
Como, Área de superficie = 4πx 2
Sea △x el cambio en el radio y △y el cambio en el área de la superficie
x = 9
△x = 0,03 m = 3 cm
x+△x = 9+3 = 12cm
= 4πx 2 = 4π(9) 2 = 324 π
= 8πx
= 8π(9) = 72π
△y = dy =
dx
△y = (72π) △x
△y = (72π) (3) = 216 π
Por lo tanto, el error aproximado en el área superficial de la esfera es 216 π cm 2
Pregunta 14: Encuentra el cambio aproximado en el área de la superficie de un cubo como lado x metros causado por la disminución del lado en un 1%.
Solución:
Según la condición dada,
Como, Área de superficie = 6x 2
Sea △x el cambio en la longitud y △y el cambio en el área de la superficie
△x/x × 100 = 1
= 6(2x) = 12x
△y =
△x
△y = (12x) (x/100)
△y = 0,12 x 2
Por lo tanto, el cambio aproximado en el área de superficie de una caja cúbica es 0.12 x 2 m 2
Pregunta 15: Si el radio de una esfera se mide como 7 m con un error de 0,02 m, encuentre el error aproximado al calcular su volumen.
Solución:
Según la condición dada,
Como, Volumen de la esfera =
πx 3
Sea △x el error en el radio y △y el error en el volumen
x = 7
△x = 0,02 cm
π(3x 2 ) = 4πx 2
= 4π(7) 2 = 196π
△y = dy =
dx
△y = (196π) △x
△y = (196π) (0,02) = 3,92 π
Por lo tanto, el error aproximado en el volumen de la esfera es 3,92 π cm 2
Pregunta 16: Encuentra el cambio aproximado en el volumen de un cubo como lado x metros causado por aumentar el lado en un 1%.
Solución:
Según la condición dada,
Como, Volumen del cubo = x 3
Sea △x el cambio en la longitud y △y el cambio en el volumen
△x/x × 100 = 1
= 3×2
△y =
△x
△y = (3x 2 ) (x/100)
△y = 0.03×3
Por lo tanto, el cambio aproximado en el volumen de una caja cúbica es 0.03 x 3 m 3