Pregunta 1. Discutir la aplicabilidad del Teorema de Rolle para las siguientes funciones en los intervalos indicados:
(i) f(x) = 3 + (x – 2) 2/3 en [1, 3]
Solución:
El teorema de Rolle establece que si una función f es continua en el intervalo cerrado [a, b] y
diferenciable en el intervalo abierto (a, b) tal que f(a) = f(b), entonces f′(x) = 0 para alguna x con a ≤ x ≤ b.
Tenemos, f'(x) =
⇒ f'(x) =
⇒ f'(x) =
⇒ f'(x) =
Para analizar la diferenciabilidad en x = 2:
⇒ f'(2) =
= 2 / 0 ≠ 0
Como f'(2) ≠ 0, f(x) no es diferenciable en el intervalo [1, 3].
Por lo tanto, el Teorema de Rolle no es aplicable para la función dada f(x) en el intervalo [1, 3].
(ii) f(x) = [x] para -1 ≤ x ≤ 1, donde [x] denota el entero mayor que no excede x
Solución:
El teorema de Rolle requiere que una función sea continua en el intervalo cerrado [a, b].
La continuidad de f(x) necesita ser analizada en x = 1:
(RHL en x = 1) = límite x⇢(1+h) [x]
= lím h⇢0 [1 + h]
= 1 ….. (1)
(LHL en x = 1) = límite x⇢(1-h) [x]
= lím h⇢0 [1 – h]
= 0 …… (2)
Dado que f(x) no es continua en x = 1 o el intervalo [-1, 1].
Por lo tanto, el Teorema de Rolle no es aplicable para la función dada f(x) en el intervalo [-1, 1].
(iii) f(x) = sin(1/x) para -1 ≤ x ≤ 1
Solución:
El teorema de Rolle requiere que una función sea continua en el intervalo cerrado [a, b].
La continuidad de f(x) necesita ser analizada en x = 0:
(RHL en x = 0) = lím x⇢(0+h) sin(1/x)
= lím h⇢0 sen(1/h)
= k…..(1)
(LHL en x = 0) = lím x⇢(0-h) sin(1/x)
= lím h⇢0 sin(1/0-h)
= lím h⇢0 sen(-1/h)
= -lím h⇢0 sen(1/h)
= −k ….(2)
Dado que f(x) no es continua en x = 1 o el intervalo [-1,1].
Por lo tanto, el Teorema de Rolle no es aplicable para la función dada f(x) en el intervalo [-1, 1].
(iv) f(x) = 2x 2 – 5x + 3 en [1, 3]
Solución:
Claramente f(x) siendo una función polinomial será continua en el intervalo.
Necesitamos verificar si f(a) = f(b) para la aplicabilidad del teorema.
Aquí, f(1) = 2(1) 2 – 5(1) + 3
⇒ f(1) = 2 – 5 + 3
⇒ f(1) = 0 …… (1)
Ahora, f(3) = 2(3) 2 – 5(3) + 3
⇒ f(3) = 2(9) – 15 + 3
⇒ f(3) = 18 – 12
⇒ f(3) = 6 …… (2)
De la ecuación (1) y (2), podemos decir que, f(1) ≠ f(3).
Observamos que f(a) ≠ f(b)
Por lo tanto, el Teorema de Rolle no es aplicable para la función dada f(x) en el intervalo [1, 3].
(v) f (x) = x 2/3 en [-1, 1]
Solución:
El teorema de Rolle establece que si una función f es continua en el intervalo cerrado [a, b] y
diferenciable en el intervalo abierto (a, b) tal que f(a) = f(b), entonces f′(x) = 0 para alguna x con a ≤ x ≤ b.
f'(x) =
⇒ f'(x) =
Claramente f'(x) no está definido en x = 0.
Por lo tanto, el Teorema de Rolle no es aplicable para la función dada f(x) en el intervalo [-1, 1].
(vi) 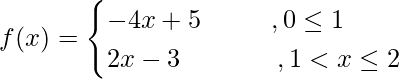
Solución:
El teorema de Rolle requiere que una función sea continua en el intervalo cerrado [a, b].
La continuidad de f(x) necesita ser analizada en x = 1:
(LHL en x = 1) = lím (x->1-h) (-4x + 5)
= lím (h->0) [-4(1 – h) + 5]
= -4 + 5
= 1
(RHL en x = 1) = lím (x->1+h) (2x – 3)
= lím (h->0) [2(1 + h) – 3]
= 2(0) – 3
= -1
Observamos que LHL ≠ RHL.
Claramente f(x) no es continua en x = 1.
Por lo tanto, el Teorema de Rolle no es aplicable para la función f(x) en el intervalo [-1, 1].
Pregunta 2. Verifique el Teorema de Rolle para cada una de las siguientes funciones en los intervalos indicados:
(i) f (x) = x 2 – 8x + 12 en [2, 6]
Solución:
La función dada es f (x) = x 2 – 8x + 12 en [2, 6].
Dado que, dado que la función f es un polinomio, es continua y derivable en todas partes, es decir, en R.
Solo necesitamos comprobar si f(a) = f(b) o no.
Así, f(2) = 2 2 – 8(2) + 12
⇒ f(2) = 4 – 16 + 12
⇒ f(2) = 0
Ahora, f(6) = 6 2 – 8(6) + 12
⇒ f(6) = 36 – 48 + 12
⇒ f(6) = 0
Como f(2) = f(6), el teorema de Rolle es aplicable para la función f(x) en [2, 6].
f(x) = x2 – 8x + 12
f'(x) = 2x – 8
Entonces f'(c) = 0
2c – 8 = 0
c = 4 ∈ (2, 6)
Por lo tanto, se verifica el teorema de Rolle
(ii) f(x) = x 2 – 4x + 3 en [1, 3]
Solución:
La función dada es f (x) = x 2 – 4x + 3 en [1, 3]
Dado que, dado que la función f es un polinomio, es continua y derivable en todas partes, es decir, en R.
Solo necesitamos comprobar si f(a) = f(b) o no.
Entonces f (1) = 1 2 – 4(1) + 3
⇒ f (1) = 1 – 4 + 3
⇒ f (1) = 0
Ahora, f (3) = 3 2 – 4(3) + 3
⇒ f (3) = 9 – 12 + 3
⇒ f (3) = 0
∴ f (1) = f(3), teorema de Rolle aplicable a la función ‘f’ en [1, 3].
⇒ f'(x) = 2x – 4
Tenemos f'(c) = 0, c ϵ (1, 3), de la definición del Teorema de Rolle.
⇒ f'(c) = 0
⇒ 2c – 4 = 0
⇒ 2c = 4
⇒ c = 4/2
⇒ c = 2 ∈ (1, 3)
Por lo tanto, se verifica el teorema de Rolle.
(iii) f (x) = (x – 1) (x – 2) 2 en [1, 2]
Solución:
La función dada es f (x) = (x – 1) (x – 2) 2 en [1, 2]
Dado que, dado que la función f es un polinomio, es continua y diferenciable en cualquier lugar que esté en R.
Solo necesitamos comprobar si f(a) = f(b) o no.
Entonces f (1) = (1 – 1) (1 – 2) 2
⇒ f(1) = 0(1) 2
⇒ f (1) = 0
Ahora, f (2) = (2 – 1)(2 – 2) 2
⇒ f (2) = 0 2
⇒ f (2) = 0
Como f (1) = f (2), el Teorema de Rolle es aplicable a la función f(x) en [1, 2].
f(x) = (x – 1)(x – 2) 2
f'(x) = (x – 1) × 2(x – 2) + (x – 2) 2
f'(x) = (x – 2) (3x – 4)
Entonces f'(c) = 0
(c – 2)(3c – 4) = 0
c = 2
o
c = 4/3 ∈ (1, 2)
Por lo tanto, se verifica el teorema de Rolle.
(iv) f (x) = x (x – 1) 2 en [0, 1]
Solución:
La función dada es f (x) = x(x – 1) 2 en [0, 1]
Dado que la función f dada es un polinomio, es continua y diferenciable en todas partes, es decir, en R.
Solo necesitamos comprobar si f(a) = f(b) o no.
Entonces f (0) = 0 (0 – 1) 2
⇒ f (0) = 0
Ahora f (1) = 1 (1 – 1) 2
⇒ f (1) = 0 2
⇒ f (1) = 0
Dado que f (0) = f (1), el teorema de Rolle aplicable para la función f (x) en [0, 1].
f (x) = x (x – 1) 2
f'(x) = (x – 1) 2 + x × 2(x – 1)
= (x – 1)(x – 1 + 2x)
= (x – 1)(3x – 1)
Entonces f'(c) = 0
(c – 1)(3c – 1) = 0
c = 1 o 1/3 ∈ (0, 1)
Por lo tanto, se verifica el teorema de Rolle.
(v) f (x) = (x 2 – 1) (x – 2) en [-1, 2]
Solución:
La función dada es f (x) = (x 2 – 1) (x – 2) en [– 1, 2]
Dado que, dado que la función f es un polinomio, es continua y diferenciable en cualquier lugar que esté en R.
Solo necesitamos comprobar si f(a) = f(b) o no.
Entonces f(–1) = (( – 1) 2 – 1)( – 1 – 2)
⇒ f (-1) = (1-1)(-3)
⇒ f (-1) = (0)(-3)
⇒ f (-1) = 0
Ahora, f (2) = (2 2 – 1)(2 – 2)
⇒ f (2) = (4 – 1)(0)
⇒ f (2) = 0
∴ f (– 1) = f (2), teorema de Rolle aplicable a la función f en [ – 1, 2].
⇒ f'(x) = 3x 2 – 4x – 1
Tenemos f'(c) = 0 c ∈ (-1, 2), de la definición del Teorema de Rolle.
Claramente, f'(c) = 0
3c 2 – 4c – 1 = 0
c = (2 ±√7)/ 3
c = 1/3(2 + √7) o 1/3(2 – √7) ∈ (-1, 2)
Por lo tanto, se verifica el teorema de Rolle.
(vi) f(x) = x(x – 4) 2 en [0, 4]
Solución:
La función dada es f (x) = x(x – 4) 2 en [0, 4]
Dado que, dado que la función f es un polinomio, es continua y derivable en todas partes, es decir, en R.
Solo necesitamos comprobar si f(a) = f(b) o no.
Entonces f (0) = 0 (0 – 4) 2
⇒ f (0) = 0
Ahora, f (4) = 4(4 – 4) 2
⇒ f(4) = 4(0) 2
⇒ f (4) = 0
Como f (0) = f (4), el teorema de Rolle es aplicable para la función f(x) en [0, 4].
f(x) = x(x – 4) 2
f'(x) = x × 2(x – 4) + (x – 4) 2
= 2x 2 – 8x + x2 + 16 – 8x
= 2x 2 – 16x + 16
Después
f'(c) = 2c 2 – 16c + 16
= (c – 4)(3c – 4)
c = 4 o 4/3 ∈ (0, 4)
Por lo tanto, se verifica el teorema de Rolle.
(vii) f (x) = x(x – 2) 2 en [0, 2]
Solución:
La función dada es f (x) = x(x – 2) 2 en [0, 2].
Dado que, dado que la función f es un polinomio, es continua y diferenciable en cualquier lugar que esté en R.
Solo necesitamos comprobar si f(a) = f(b) o no.
Entonces f (0) = 0(0 – 2) 2
⇒ f (0) = 0
Ahora, f (2) = 2(2 – 2) 2
⇒ f(2) = 2(0) 2
⇒ f (2) = 0
f (0) = f(2), teorema de Rolle aplicable a la función f en [0,2].
c = 12/6 o 4/6
c = 2 o 2/3
Entonces, c = 2/3 ya que c ∈ (0, 2)
Por lo tanto, se verifica el teorema de Rolle.
(viii) f (x) = x 2 + 5x + 6 en [-3, -2]
Solución:
La función dada es f (x) = x 2 + 5x + 6 en [– 3, – 2].
Dado que, dado que la función f es un polinomio, es continua y derivable en todas partes, es decir, en R.
Solo necesitamos comprobar si f(a) = f(b) o no.
Entonces f(–3) = (–3) 2 + 5(–3) + 6
⇒ f(–3) = 9 – 15 + 6
⇒ f(–3) = 0
Ahora, f(–2) = (–2) 2 + 5(–2) + 6
⇒ f(–2) = 4 – 10 + 6
⇒ f(–2) = 0
Como f(–3) = f(–2), el teorema de Rolle es aplicable a la función f(x) en [–3, –2].
f(x) = x2 + 5x + 6
f'(x) = 2x + 5
Después
f(c) = 0
2c + 5 = 0
c = -5/2 ∈ (-3, -2)
Por lo tanto, se verifica el teorema de Rolle.
Pregunta 3. Verifique el Teorema de Rolle para cada una de las siguientes funciones en los intervalos indicados:
(i) f(x) = cos2(x – π/4) en [0, π/2]
Solución:
Claramente, la función coseno es continua y diferenciable en todas partes.
Por tanto, la función dada f(x) es continua en [0, π/2] y derivable en [0, π/2]
Asi que,
f(0) = cos2(0 – π/4) = 0
f(π/2) = cos2(π/2 – π/4) = 0
Como f(0) = f(π/2), el teorema de Rolle aplicable para la función f(x) en [0, π/2].
Ahora, f'(x) =
= -2sen(2x – π/2)
Si f'(c) = 0
⇒ -2sen(2c – π/2) = 0
⇒ c = π/4 ∈ [0, π/2]
Claramente c pertenece al intervalo dado.
Por lo tanto, se verifica el teorema de Rolle.
(ii) f(x) = sen 2x en [0, π/2]
Solución:
Como sen 2x es continuo y diferenciable en todas partes.
Entonces, sen2x es continua en (0, π/2) y diferenciable en (0, π/2).
f(0) = sen 0 = 0
f(π/2) = sen π/2 = 0
f(π/2) = f(0) = 0
Por tanto, f(x) satisface todas las condiciones del teorema de Rolle.
Ahora, tenemos que demostrar que existe c en (0, π/2) tal que f'(c) = 0.
Tenemos, f'(x) = 0
⇒cos2x = 0
⇒ x = π/4
Entonces, f'(c) = 2cos2c
2cos2c = 0
Así, c = π/4 en (0, π/2).
Por lo tanto, se verifica el teorema de Rolle.
(iii) f(x) = cos2x en [-π/4, π/4]
Solución:
Como cos 2x es continuo y diferenciable en todas partes.
Entonces, cos2x es continua en [-π/4, π/4] y derivable en [-π/4, π/4].
cos(-π/4) = cos2(-π/4) = cos(-π/2) = 0
cos(π/4) = cos2(π/4) = cos(π/2) = 0
Además, cos(-π/4) = cos(π/4)
Por tanto, f(x) satisface todas las condiciones del teorema de Rolle.
Ahora, tenemos que demostrar que existe c en (0, π/2) tal que f'(c) = 0.
Tenemos f'(x) = 0
⇒ sen2c = 0
⇒ 2c = 0
Entonces, c = 0 cuando c ∈ (-π/4, π/4)
Por lo tanto, el Teorema de Rolle se verifica para la función dada f(x).
(iv) e x sen x en [0, π]
Solución:
La función dada es una composición de funciones exponenciales y trigonométricas. Por lo tanto, es diferencial y continuo en todas partes.
Entonces, la función dada f(x) es continua en [0, π] y diferenciable en (0, π).
f(0) = e 0 sen 0 = 0
f(π) = mi π sen π = 0
f(0) = f(π)
Ahora, tenemos que demostrar que existe c en (0, π) tal que f'(c) = 0.
Entonces f'(x) = e x (sen x + cos x)
⇒ e x (sen x + cos x) = 0
⇒ sen x + cos x = 0
Dividiendo ambos lados por cos x, tenemos
tan x = -1
⇒ x = π – π/4 = 3π/4
Como c = 3π/4 en (0, π) tal que f'(c) = 0.
Por lo tanto, el teorema de Rolle se verifica para la función dada f(x).
(v) f(x) = e x cos x en [−π/2, π/2]
Solución:
La función dada es una composición de funciones exponenciales y trigonométricas. Por lo tanto, es diferencial y continuo en todas partes.
Entonces, la función dada f(x) es continua en [-π/2, π/2] y diferenciable en (-π/2, π/2).
f(−π/2) = e π/2 cos(−π/2) = 0
f(π/2) = e π/2 cos(π/2) = 0
f(−π/2) = f(π/2)
Ahora, tenemos que demostrar que existe c en (-π/2, π/2) tal que f'(c) = 0.
f'(x) = e x (cos x – sen x)
⇒ e x (cos x – sen x) = 0
⇒ sen x – cos x = 0
Dividiendo ambos lados por cos x, tenemos
bronceado x = 1
⇒ x = π/4
Como c = π/4 en (-π/2, π/2) tal que f'(c) = 0.
Por lo tanto , el teorema de Rolle se verifica para la función dada f(x).
(vi) f (x) = cos 2x en [0, π]
Solución:
Como cos 2x es continuo y diferenciable en todas partes.
Entonces, cos2x es continua en [0, π] y diferenciable en (0, π).
f(0) = cos(0) = 1
f(π) = cos(2π) = 1
f(0) = f(π)
Por tanto, f(x) satisface todas las condiciones del teorema de Rolle.
Debe haber ac perteneciente a (0, π) tal que f'(c) = 0.
⇒ sen 2c = 0
Entonces, 2c = 0 o π
c = 0 o π/2
Pero, c = π/2 cuando c ∈ (0, π)
Por lo tanto, el Teorema de Rolle se verifica para la función dada f(x).
(vii) f(x) = senx/e x en 0 ≤ x ≤ π
Solución:
La función dada es una composición de funciones exponenciales y trigonométricas.
Por lo tanto, es diferencial y continuo en todas partes.
Entonces, senx/ex es continua en [0, π] y derivable en (0, π).
f(0) = sen(0)/e 0 = 0
f(π) = sen(π)/e π = 1
f(0) = f(π)
Ahora, tenemos que demostrar que existe c en (0, π/2) tal que f'(c) = 0.
f'(x) = e x (cos x – sen x)
⇒ e x (cos x – sen x) = 0
⇒ sen x – cos x = 0
⇒ tan x = 1
⇒x = π/4
Como c = π/4 en (-π/4, π/4) tal que f'(c) = 0.
Por lo tanto, el teorema de Rolle se verifica para la función dada f(x).
(viii) f(x) = sen 3x en [0, π]
Solución:
La función dada es f (x) = sin3x en [0, π]
Como la función seno es continua y diferenciable en R.
Necesitamos comprobar si f(a) = f(b) o no.
Entonces f (0) = sen 3(0)
⇒ f (0) = sin0
⇒ f (0) = 0
Ahora, f (π) = sen 3π
⇒ f (π) = sen(3 π)
⇒ f (π) = 0
Tenemos f (0) = f (π), entonces existe ac perteneciente a (0, π) tal que f'(c) = 0.
⇒ 3cos(3x) = 0
⇒ cos 3x = 0
⇒ 3x = π / 2
⇒ x = π / 6 ∈ [0, π]
Por lo tanto, el teorema de Rolle se verifica para la función dada f(x).
(ix) f(x) = 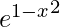 en [−1, 1]
en [−1, 1]
Solución:
Sabemos que la función exponencial es continua y diferenciable en todas partes.
Entonces,
es continua en [-1, 1] y diferenciable en (-1, 1).
f(-1) = mi 1-1 = 1
f(1) = mi 1-1 = 1
Además, f(-1) = f(1) = 1
Por lo tanto, el teorema de Rolle es aplicable. Entonces debe existir c ∈ [−1, 1] tal que f'(c) = 0.
f'(x) =
⇒ -2x e^{1 – x^2} = 0
⇒ x = 0 ∈ [−1, 1]
Por lo tanto , se verifica el teorema de Rolle.
(x) f (x) = log (x 2 + 2) – log 3 en [-1, 1]
Solución:
Claramente, la función logarítmica es continua y diferenciable en su propio dominio.
Necesitamos verificar si f(a) = f(b) o no.
Entonces f (– 1) = log((– 1) 2 + 2) – log 3
⇒ f (– 1) = registro (1 + 2) – registro 3
⇒ f (– 1) = logaritmo 3 – logaritmo 3
⇒ f (-1) = 0
Ahora, f (1) = log (1 2 + 2) – log 3
⇒ f (1) = logaritmo (1 + 2) – logaritmo 3
⇒ f (1) = logaritmo 3 – logaritmo 3
⇒ f (1) = 0
Tenemos f (– 1) = f (1).
Entonces, existe ac tal que c ϵ (– 1, 1) tal que f'(c) = 0.
Ahora, f'(x) =
f'(c) = 0
⇒ c = 0 ϵ (– 1, 1)
Por lo tanto, se verifica el teorema de Rolle.
(xi) f(x) = sen x + cos x en [0, π/2]
Solución:
Como las funciones seno y coseno son continuas y diferenciables en todas partes,
f(x) es continua en [0, π/2] y derivable en (0, π/2).
Entonces, f(0) = sen 0 + cos 0 = 1
f(π/2) = sen π/2 + cos π/2 = 1
Además, f(0) = f(π/2) = 1.
Por lo tanto, el teorema de Rolle es aplicable. Entonces debe existir c ∈ [−1, 1] tal que f'(c) = 0.
Ahora, f'(x) = cos x – sen x
⇒ cos x – sen x = 0
⇒ tan x = 1
⇒ x = π/4
Por lo tanto, c = π/4 en (0, π/2).
Por lo tanto, el teorema de Rolle se verifica para la función dada f(x).
(xii) f (x) = 2 sen x + sen 2x en [0, π]
Solución:
Dado que sen es una función continua y derivable sobre R, f(x) es continua sobre [0, π] y derivable sobre (0, π).
Necesitamos verificar si f(a) = f(b) o no.
Entonces f (0) = 2sin(0) + sin2(0)
⇒ f(0) = 2(0) + 0
⇒ f (0) = 0
Ahora, f (π) = 2sin(π) + sin2(π)
⇒ f (π) = 2(0) + 0
⇒ f (π) = 0
Tenemos f (0) = f (π), entonces existe ac perteneciente a (0, π) tal que f'(c) = 0.
f'(x) = 2 cos x + cos 2x
Ahora, f'(c) = 0
⇒ 2 cos x + cos 2x = 0
⇒ (2cos c – 1) (cos c + 1) = 0
⇒ bronceado c = 1
⇒ c = π/3 en (0, π)
Por lo tanto, el teorema de Rolle se verifica para la función dada f(x).
(xiii) f(x) = ![Rendered by QuickLaTeX.com \frac{x}{2} - \sin[\frac{\pi x}{6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6ca6d37d4bb2b8131b8b7b24f8513044_l3.png) en [-1, 0]
en [-1, 0]
Solución:
Como la función sen es continua y diferenciable en R, f(x) es continua en [-1, 0] y derivable en (-1, 0).
f(-1) =
= 0
f(0) = 0 – sen 0 = 0
También f(-1) = f(0) = 0
Por lo tanto, el teorema de Rolle es aplicable para que exista ac perteneciente a (0, π) tal que f'(c) = 0.
f'(x) =
Ahora, f'(c) = 0
⇒
⇒
⇒ c =
Por lo tanto, c ϵ (-1, 0).
Por lo tanto, el teorema de Rolle se verifica para la función dada f(x).
(xiv) f(x) = 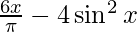 en [0, π/6]
en [0, π/6]
Solución:
Dado que la función sin es continua y derivable en todas partes, f(x) es continua en [0, π/6] y derivable en (0, π/6).
f(0) = 0 – 0 = 0
f(π/6) = 1 – 1 = 0
Además, f(0) = f(π/6) = 0
Por lo tanto, el teorema de Rolle es aplicable para que exista ac perteneciente a (0, π/6) tal que f'(c) = 0.
Tenemos, f'(x) = 6/π – 8senxcosx
f'(x) = 6/π – 4sen2x
f'(c) = 0
6/π – 4sen2c = 0
4sen2c = 6/π
sen2c = 3/2π
2c = sen -1 (21/44)
c = 1/2 sen -1 (21/44)
do ∈ (-1/2, 1/2)
c ∈ (0, 21/11)
c ∈ (0, π/6)
Por lo tanto, el teorema de Rolle se verifica para la función dada f(x).
(xv) f(x) = 4 sen x en [0, π]
Solución:
Como las funciones sin y exponencial son continuas y derivables en todas partes, f(x) es continua en [0, π] y derivable en (0, π).
f(0) = 4 sen 0 = 1
f(π) = 4 sen π = 1
Además, f(0) = f(π) = 1.
Por lo tanto, el teorema de Rolle es aplicable para que exista ac perteneciente a (0, π) tal que f'(c) = 0.
Tenemos, f'(x) = 4sen x cos x log 4
Entonces, f'(c) = 0
4 sen c cos c log 4 = 0
4sen c cos c = 0
porque c = 0
c = π/2 ∈ (0, π)
Por lo tanto, el teorema de Rolle se verifica para la función f(x) dada.
(xvi) f (x) = x 2 – 5x + 4 en [1, 4]
Solución:
Dado que, dado que la función f es un polinomio, es continua y derivable en todas partes, es decir, en R.
Necesitamos verificar si f(a) = f(b) o no.
Entonces f (1) = 1 2 – 5(1) + 4
⇒ f (1) = 1 – 5 + 4
⇒ f (1) = 0
Ahora, f (4) = 4 2 – 5(4) + 4
⇒ f (4) = 16 – 20 + 4
⇒ f (4) = 0
Tenemos f (1) = f (4). Entonces, existe ac ∈ (1, 4) tal que f'(c) = 0.
f'(x) = 2x – 5
Ahora, f'(c) = 2c – 5 = 0
Así, c = 5 / 2 ∈ (1, 4).
Por lo tanto, el teorema de Rolle se verifica para la función f(x) dada.
(xvii) f(x) = sen 4 x + cos 4 x en (0, π/2)
Solución:
Dado que las funciones seno y coseno son continuas y derivables en todas partes, f(x) es continua en [0, π/2] y derivable en (0, π/2).
Asi que,
f(0) = sen 4 (0) + cos 4 (0) = 1
f(π/2) = sen 4 (π/2) + cos 4 (π/2) = 1
f(0) = f(π/2)
Por lo tanto, el teorema de Rolle es aplicable para que exista ac perteneciente a (0, π/2) tal que f'(c) = 0.
⇒ f'(x) = 4sen 3 x cos x – 4cos 3 x sen x
entonces, f'(c) = 4sen 3 x cos x – 4cos 3 x sen x = 0
4sen 3 c cos c – 4cos 3 c sen c = 0
-sin4c = 0
4x = 0 o 4x = π
x = 0, o π/4 ∈ (0, π/2)
Por lo tanto, se verifica el teorema de Rolle.
(xviii) f(x) = sen x – sen 2x en [0, π]
Solución:
La función dada es f (x) = sen x – sen2x en [0, π]
Sabemos que la función seno es continua y derivable sobre R.
Ahora tenemos que comprobar los valores de la función ‘f’ en los extremos.
⇒ f (0) = sen (0) – sen 2(0)
⇒ f (0) = 0 – sen (0)
⇒ f (0) = 0
⇒ f (π) = sen(π) – sen2(π)
⇒ f (π) = 0 – sin(2π)
⇒ f (π) = 0
Tenemos f (0) = f (π). Entonces, existe ac ∈ (0, π) tal que f'(c) = 0.
f'(x) = cos x – 2 cos 2x
entonces, f'(c) = 0
f'(c) = cos c – 2 cos 2c = 0
cos c – (2 cos 2 c + 1) = 0
2cos 2 c – cosc – 1 = 0
(cos c – 1)(2 cos c + 1) = 0
porque c = 1, -1/2
c = cos(π/2), cos(2π/3)
Entonces, c = π/2, 2π/3 ∈ (0, π)
Por lo tanto, se verifica el teorema de Rolle.
Pregunta 4. Usando el teorema de Rolle, encuentra puntos en la curva y = 16 – x2, x ∈ [-1, 1], donde la tangente es paralela al eje x.
Solución:
Dado: y = 16 – x 2 , x ϵ [– 1, 1]
⇒ y (– 1) = 16 – (– 1) 2
⇒ y (– 1) = 16 – 1
⇒ y (– 1) = 15
Ahora, y (1) = 16 – (1) 2
⇒ y (1) = 16 – 1
⇒ y (1) = 15
Tenemos y (– 1) = y (1). Entonces, existe ac ϵ (– 1, 1) tal que f'(c) = 0.
Sabemos que para una curva g, el valor de la pendiente de la tangente en un punto r viene dado por g'(r).
⇒ y’ = –2x
Tenemos y'(c) = 0
⇒ – 2c = 0
⇒ c = 0 ϵ (– 1, 1)
El valor de y en x = 1 es
⇒ y = 16 – 02
⇒ y = 16
Por lo tanto, el punto en el que la curva y tiene una tangente paralela al eje x (ya que la pendiente del eje x es 0) es (0, 16).
Pregunta 5. ¿En qué puntos de las siguientes curvas la tangente es paralela al eje x?
(i) y = x 2 en [-2, 2]
Solución:
Dado: f(x) = x 2
f'(x) = 2x
Además, f(-2) = f(2) = 2 2 = (-2) 2 = 4
Entonces, existe ac ϵ (-2, 2) tal que f'(c) = 0.
⇒ 2c = 0
⇒ c = 0
Por lo tanto, el punto requerido es (0, 0).
(ii) y = 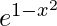 en [−1, 1]
en [−1, 1]
Solución:
Dado que la función exponencial es continua y diferenciable en todas partes.
Aquí f(1) = f(-1) = 1
Por tanto, se cumplen todas las condiciones del teorema de Rolle.
En consecuencia, existe al menos un punto c en (-1, 1) para el cual f'(c) = 0.
⇒ f'(c) = 0
⇒ -2c e^{1 – c^2} = 0
⇒ c = 0
Por lo tanto, (0, e) es el punto requerido.
(iii) y = 12 (x + 1) (x − 2) en [−1, 2]
Solución:
Dado que la función polinomial es continua y diferenciable en todas partes.
Aquí f(2) = f(-1) = 0.
Por tanto, se cumplen todas las condiciones del teorema de Rolle.
En consecuencia, existe al menos un punto c en (-1, 2) para el cual f'(c) = 0.
Pero f'(c) = 0
⇒ 24c – 12 = 0
⇒ c = 1/2
Por lo tanto, (1/2, -27) es el punto requerido.
Pregunta 6. Si f: [5, 5] a R es una función diferenciable y si f'(x) no se anula en ninguna parte, demuestre que f(-5) ≠ f(5).
Solución:
Aquí f(x) es diferenciable en (5,5).
Por el teorema del valor medio,
⇒ 10 f'(c) = f(5) – f(-5)
También se da que f'(x) no desaparece en ninguna parte.
⇒ f'(c) ≠ 0
⇒ 10 f'(c) ≠ 0
⇒ f(5) – f(-5) ≠ 0
⇒ f(5) ≠ f(-5)
Por lo tanto probado
Pregunta 7. Examine si el teorema de Rolle es aplicable a alguna de las siguientes funciones.
(i) f (x) = [x] para x ∈ [5, 9]
(ii) f (x) = [x] para x ∈ [−2, 2]
¿Puedes decir algo sobre el inverso del teorema de Rolle a partir de estas funciones?
Solución:
El teorema de Rolle establece que si una función f es continua en el intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b) tal que f(a) = f(b), entonces f′(x) = 0 para alguna x con a ≤ x ≤ b.
(i) f(x) = [x] para x ∈ [ 5 , 9 ]
f(x) no es continua en x = 5 y x = 9. Por lo tanto, f (x) no es continua en [5, 9].
Además, f (5) = [5] = 5 y f (9) = [9] = 9
∴ f (5) ≠ f (9)
El límite izquierdo de f en x = n es ∞ y el límite derecho de f en x = n es 0.
Como los límites izquierdo y derecho de f en x = n no son iguales, f no es derivable en (5, 9).
Por tanto, el teorema de Rolle no es aplicable a la función f(x) para x ∈ [5 , 9].
(ii) f (x) = [x] para x ∈ [-2, 2]
f(x) no es continua en x = −2 y x = 2. Por lo tanto, f (x) no es continua en [−2, 2].
Además, f (-2) = [-2] = -2 y f (2) = [2] = 2
∴ f (-2) ≠ f (2)
El límite izquierdo de f en x = n es ∞ y el límite derecho de f en x = n es ∞.
Dado que los límites izquierdo y derecho de f en x = n no son iguales, f no es derivable en (−2, 2).
Por tanto, el teorema de Rolle no es aplicable a la función f(x) = [x] para x ∈ [ -2, 2].
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA