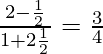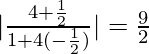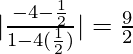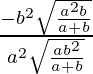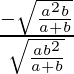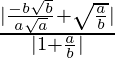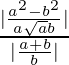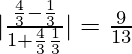Pregunta 1. Encuentra el ángulo de intersección de las siguientes curvas:
(i) y 2 = x y x 2 = y
Solución:
La primera curva es y 2 = x. . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2y (dy/dx) = 1
=> m 1 = dy/dx = 1/2y
La segunda curva es x 2 = y . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x = dy/dx
=> m 2 = dy/dx = 2x
Resolviendo (1) y (2), obtenemos,
=> x 4 − x = 0
=> x (x 3 − 1) = 0
=> x = 0 o x = 1
Sabemos que el ángulo de intersección de dos curvas está dado por,
tan θ =
donde m 1 y m 2 son las pendientes de las curvas.
Cuando x = 0, entonces y = 0.
Entonces, m 1 = 1/2y = 1/0 = ∞
metro2 = 2x = 2(0) = 0
Por lo tanto, tan θ =
= ∞
=> θ = π/2
Cuando x = 1, entonces y = 1.
Entonces, m 1 = 1/2y = 1/2
metro2 = 2x = 2(1) = 2
Por lo tanto, tan θ =
=> θ = tan −1 (3/4)
(ii) y = x 2 y x 2 + y 2 = 20
Solución:
La primera curva es y = x 2 . . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> (dy/dx) = 2x
=> m 1 = dy/dx = 2x
La segunda curva es x 2 + y 2 = 20 . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x + 2y (dy/dx) = 0
=> m 2 = dy/dx = −x/y
Resolviendo (1) y (2), obtenemos,
=> y 2 +y − 20 = 0
=> y 2 + 5y − 4y − 20 = 0
=> (y + 5) (y − 4) = 0
=> y = −5 o y = 4
Ignorando y = − 5 cuando x se convierte en √(−5) en ese caso, lo cual no es posible.
Cuando y = 4, obtenemos x 2 = 4
=> x = ±2
Sabemos que el ángulo de intersección de dos curvas está dado por,
tan θ =
donde m 1 y m 2 son las pendientes de las curvas.
Cuando x = ±2 y y = 4, obtenemos,
m 1 = 2x = 2(2) = 4 o ±4
m2 = −x/y = −2/4 = −1/2
Entonces, tan θ =
=> θ = tan −1 (9/2)
Cuando x = −2 y y = 4, obtenemos,
m 1 = 2x = 4 o −4
m2 = −x/y = 1/2 o −1/2
Entonces, tan θ =
=> θ = tan −1 (9/2)
(iii) 2y 2 = x 3 y y 2 = 32x
Solución:
La primera curva es 2y 2 = x 3 . . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 4y (dy/dx) = 3x 2
=> m 1 = dy/dx = 3x 2 /4y
La segunda curva es y 2 = 32x. . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2y (dy/dx) = 32
=> m 2 = dy/dx = 32/2y = 16/y
Resolviendo (1) y (2), obtenemos,
=> 2(32x) = x3
=> x3 − 64x = 0
= > x(x2 − 64) = 0
=> x = 0 o x 2 − 64 = 0
=> x = 0 o x = ±8
Sabemos que el ángulo de intersección de dos curvas está dado por,
tan θ =
donde m 1 y m 2 son las pendientes de las curvas.
Cuando x = 0 entonces y = 0.
m 1 = 3x 2 /4y = ∞
metro2 = 16/año = ∞
Entonces, tan θ = ∞
=> θ = π/2
Cuando x = ±8, entonces y = ±16.
m 1 = 3x 2 /4y = 3 o −3
m2 = 16/y = 1 o −1
Entonces, tan θ =
=> θ = bronceado −1 (1/2)
(iv) x 2 + y 2 – 4x – 1 = 0 y x 2 + y 2 – 2y – 9 = 0
Solución:
La primera curva es x 2 + y 2 – 4x – 1 = 0. . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x + 2y (dy/dx) – 4 = 0
=> m 1 = dy/dx = (2–x)/y
La segunda curva es x 2 + y 2 – 2y – 9 = 0. . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x + 2y (dy/dx) – 2 (dy/dx) = 0
=> m 2 = dy/dx = –x/(y–1)
La primera curva se puede escribir como,
=> (x – 2) 2 + y 2 – 5 = 0 . . . . (3)
Restando (2) de (1), obtenemos
=> x2 + y2 – 4x – 1 – x2 – y2 + 2y + 9 = 0
=> – 4x – 1 + 2y + 9 = 0
=> 2y = 4x – 8
=> y = 2x – 4
Poniendo y = 2x – 4 en (1), obtenemos,
=> (x – 2) 2 + (2x – 4) 2 – 5 = 0
⇒ (x – 2) 2 (1 + 4) – 5 = 0
⇒ 5(x – 2) 2 – 5 = 0
⇒ (x – 2) 2 = 1
⇒ x = 3 o x = 1
Entonces, cuando x = 3 entonces y = 6 – 4 = 2
m 1 = (2–x)/y = (2–3)/2 = –1/2
m2 = –x/(y–1) = –3/(2–1) = –3
Entonces, tan θ =
= 1
=> θ = π/4
Entonces, cuando x = 1 entonces y = 2 – 4 = – 2
m 1 = (2–x)/y = (2–1)/(–2) = –1/2
m2 = –x/(y–1) = –1/(–2–1) = 1/3
Entonces, tan θ =
= 1
=> θ = π/4
(v) x 2 /a 2 + y 2 /b 2 = 1 y x 2 + y 2 = ab
Solución:
La primera curva es x 2 /a 2 + y 2 /b 2 = 1 . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x/a 2 + (2y/b 2 ) (dy/dx) = 0
=> m 1 = dy/dx = –b 2 x/a 2 y
La segunda curva es x 2 + y 2 = ab . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x + 2y (dy/dx) = 0
=> m2 = dy/dx = –2x/2y = –x/y
Resolviendo (1) y (2), obtenemos,
=> x 2 /a 2 + (ab – x 2 )/b 2 = 1
=> x 2 segundo 2 – un 2 x 2 = un 2 segundo 2 – un 3 segundo
=> x2 =
=> x =
De (2), obtenemos, y 2 =
=> y =
Entonces, m 1 = –b 2 x/a 2 y =
=
m2 = –x/y =
=
Por lo tanto, tan θ =
=> tan θ =
=> tan θ =
=> θ = tan –1 ((a–b)/√ab)
(vi) x 2 + 4y 2 = 8 y x 2 – 2y 2 = 2
Solución:
La primera curva es x 2 + 4y 2 = 8 . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x + 8y (dy/dx) = 0
=> m 1 = dy/dx = –2x/8y = –x/4y
La segunda curva es x 2 – 2y 2 = 2 . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x – 4y (dy/dx) = 0
=> m 2 = dy/dx = x/2y
Resolviendo (1) y (2), obtenemos,
6y2 = 6 => y2 = ±1
x2 = 2 + 2 => x = ±2
Entonces, tan θ =
=> θ = bronceado –1 (1/3)
(vii) x2 = 27y y y2 = 8x
Solución:
La primera curva es x 2 = 27y . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x = 27 (dy/dx)
=> m 1 = dy/dx = 2x/27
La segunda curva es y 2 = 8x . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2y (dy/dx) = 8
=> m 2 = dy/dx = 8/2y = 4/y
Resolviendo (1) y (2), obtenemos,
=> y 4 /64 = 27 años
=> y (y 3 − 1728) = 0
=> y = 0 o y = 12
Y x = 0 o x = 18.
Entonces, cuando x = 0 y y = 0
metro 1 = 0 y metro 2 = ∞
bronceado θ =
= ∞
=> θ = π/2
Entonces, cuando x = 18 y y = 12
m 1 = 2x/27 = 12/9 = 4/3 y m 2 = 4/y = 1/3
tan θ =
=> θ = tan −1 (9/13)
(viii) x 2 + y 2 = 2x y y 2 = x
Solución:
La primera curva es x 2 + y 2 = 2x . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x + 2y (dy/dx) = 2
=> m 1 = dy/dx = (1–x)/y
La segunda curva es y 2 = x . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2y (dy/dx) = 1
=> m 2 = dy/dx = 1/2y
Resolviendo (1) y (2), obtenemos,
=> x 2 – x = 0
=> x = 0 o x = 1
Y y = 0 o y = ±1.
Cuando x = 0, y = 0, m 1 = ∞ y m 2 = ∞
tan θ =
=> θ = π/2
Cuando x = 1 y y = ±1, m 1 = 0 y m 2 = 1/2
tan θ =
=> θ = bronceado −1 (1/2)
(ix) y = 4 − x 2 y y = x 2
Solución:
La primera curva es y = 4 − x 2 . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> dy/dx = −2x
=> m 1 = dy/dx = −2x
La segunda curva es y = x 2 . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> dy/dx = 2x
=> m 2 = dy/dx = 2x
Resolviendo (1) y (2), obtenemos,
=> 2×2 = 4
=> x = ±√2
y y = 2
Entonces, m 1 = −2x = −2√2 y m 2 = 2x = 2√2
tan θ =
=> θ = bronceado −1 (4√2/7)
Pregunta 2. Muestre que el siguiente conjunto de curvas se intersecan ortogonalmente:
(i) y = x 3 y 6y = 7 – x 2
Solución:
La primera curva es y = x 3 . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> dy/dx = 3x 2
=> m 1 = dy/dx = 3x 2
La segunda curva es 6y = 7 – x 2 . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 6y (dy/dx) = – 2x
=> m2 = dy/dx = –2x/6y = – x/3y
Resolviendo (1) y (2), obtenemos,
= > 6y = 7 – x2
=> 6x 3 + x 2 – 7 = 0
Como x = 1 satisface esta ecuación, obtenemos x = 1 y y = 1 3 = 1
Entonces, m 1 = 3 y m 2 = – 1/3
Dos curvas se cortan ortogonalmente si m 1 m 2 = –1
=> 3 × (–1/3) = –1
Por lo tanto probado.
(ii) x 3 – 3xy 2 = – 2 y 3x 2 y – y 3 = 2
Solución:
La primera curva es x 3 – 3xy 2 = – 2
Derivando ambos lados con respecto a x, obtenemos,
=> 3x 2 – 3y 2 – 6xy (dy/dx) = 0
=> m 1 = dy/dx = 3(x 2 –y 2 )/6xy
La segunda curva es 3x 2 y – y 3 = 2
Derivando ambos lados con respecto a x, obtenemos,
=> 6xy + 3x 2 (dy/dx) – 3y 2 (dy/dx) = 0
=> m2 = dy/dx = –6xy/3( x2 –y2 )
Dos curvas se cortan ortogonalmente si m 1 m 2 = –1
=>
= –1
Por lo tanto probado.
(iii) x 2 + 4y 2 = 8 y x 2 – 2y 2 = 4.
Solución:
La primera curva es x 2 + 4y 2 = 8 . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x + 8y (dy/dx) = 0
=> m 1 = dy/dx = 2x/8y = –x/4y
La segunda curva es x 2 – 2y 2 = 4 . . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x – 4y (dy/dx) = 0
=> m2 = dy/dx = 2x/4y = x/2y
Resolviendo (1) y (2), obtenemos,
=> x = 4/√3 y y = √2/√3
Entonces, m 1 = –x/4y = –1/√2
m2 = x/2y = √2
Dos curvas se cortan ortogonalmente si m 1 m 2 = –1
=> (–1/√2) × √2 = –1
Por lo tanto probado.
Pregunta 3. Muestre que las curvas:
(i) x 2 = 4y y 4y + x 2 = 8 se cortan ortogonalmente en (2, 1).
Solución:
La primera curva es x 2 = 4y
Derivando ambos lados con respecto a x, obtenemos,
=> 2x = 4 (dy/dx)
=> m 1 = dy/dx = 2x/4 = x/2
La segunda curva es 4y + x 2 = 8
Derivando ambos lados con respecto a x, obtenemos,
=> 4 (dy/dx) + 2x = 0
=> m 2 = dy/dx = −2x/4 =−x/2
Para x = 2 y y = 1, tenemos m 1 = 2/2 = 1 y m 2 = −x/2 = −1.
Dos curvas se cortan ortogonalmente si m 1 m 2 = –1
=> 1 × (–1) = –1
Por lo tanto, estas dos curvas se cortan ortogonalmente en (2, 1).
Por lo tanto probado.
(ii) x 2 = y y x 3 + 6y = 7 se cortan ortogonalmente en (1, 1).
Solución:
La primera curva es x 2 = y
Derivando ambos lados con respecto a x, obtenemos,
=> 2x = dy/dx
=> m 1 = dy/dx = 2x
La segunda curva es x 3 + 6y = 7
Derivando ambos lados con respecto a x, obtenemos,
=> 3x 2 + 6 (dy/dx) = 0
=> m 2 = dy/dx = −3x 2 /6 =−x 2 /2
Para x = 1 y y = 1, tenemos m 1 = 2(1) = 2 y m 2 = −(1) 2 /2 = −1/2.
Dos curvas se cortan ortogonalmente si m 1 m 2 = –1
=> 2 × (–1/2) = –1
Por lo tanto, estas dos curvas se cortan ortogonalmente en (1, 1).
Por lo tanto probado.
(iii) y 2 = 8x y 2x 2 + y 2 = 10 se cortan ortogonalmente en (1, 2√2).
Solución:
La primera curva es y 2 = 8x
Derivando ambos lados con respecto a x, obtenemos,
=> 2y (dy/dx) = 8
=> m 1 = dy/dx = 8/2y = 4/y
La segunda curva es 2x 2 + y 2 = 10
Derivando ambos lados con respecto a x, obtenemos,
=> 4x + 2y (dy/dx) = 0
=> m 2 = dy/dx = −4x/2y =−2x/y
Para x = 1 y y = 2√2, tenemos m 1 = 4/2√2 = √2 y m 2 = −2/2√2 = −1/√2
Dos curvas se cortan ortogonalmente si m 1 m 2 = –1
=> √2 × (−1/√2) = –1
Por lo tanto, estas dos curvas se cortan ortogonalmente en (1, 2√2).
Por lo tanto probado.
Pregunta 4. Muestre que las curvas 4x = y 2 y 4xy = k cortan en ángulo recto, si k 2 = 512.
Solución:
La primera curva es 4x = y 2 . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2y (dy/dx) = 4
=> m 1 = dy/dx = 4/2y = 2/y
La segunda curva es 4xy = k. . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> y + x (dy/dx) = 0
=> m 2 = dy/dx = −y/x
Resolviendo (1) y (2), obtenemos,
=> y 3 = k
=> y = k 1/3
Entonces, x = k 2/3/4
Como las curvas se cortan en ángulo recto, m 1 m 2 = –1
=> (2/año) × (−y/x) = –1
=> 2/x = 1
=> 8/k 2/3 = 1
=> k 2/3 = 8
=> k2 = 512
Por lo tanto probado.
Pregunta 5. Muestre que las curvas 2x = y 2 y 2xy = k cortan en ángulo recto, si k 2 = 8.
Solución:
La primera curva es 2x = y 2 . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2y (dy/dx) = 2
=> m 1 = dy/dx = 2/2y = 1/y
La segunda curva es 2xy = k. . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> y + x (dy/dx) = 0
=> m 2 = dy/dx = −y/x
Resolviendo (1) y (2), obtenemos,
=> y 3 = k
=> y = k 1/3
Entonces, x = k 2/3/2
Como las curvas se cortan en ángulo recto, m 1 m 2 = –1
=> (1/año) × (−y/x) = –1
=> 1/x = 1
=> 2/k 2/3 = 1
=> k 2/3 = 2
=> k2 = 8
Por lo tanto probado.
Pregunta 6. Demuestra que las curvas xy = 4 y x 2 + y 2 = 8 se tocan entre sí.
Solución:
Tenemos,
xy = 4 . . . . (1)
x 2 + y 2 = 8 . . . . (2)
Resolviendo (1) y (2), obtenemos,
=> (4/año) 2 + y 2 = 8
=> y 4 − 8y 2 + 16 = 0
=> (y 2 − 4) 2 = 0
=> y = ±2
Y obtenemos x = ±2.
Ecuación diferencial. (1) con respecto a x, obtenemos,
=> y + x (dy/dx) = 0
=> m 1 = dy/dx = −y/x
Ecuación diferencial. (2) con respecto a x, obtenemos,
=> 2x + 2y (dy/dx) = 0
=> dy/dx = −x/y
En x = 2 y y = 2, tenemos,
m 1 = −2/2 = −1 y también m 2 = −2/2 = −1. Por lo tanto m 1 = m 2 .
También en x = −2 y y = −2, tenemos m 1 = m 2
Entonces, podemos decir que las curvas se tocan en (2, 2) y (−2, −2).
Por lo tanto probado.
Pregunta 7. Demuestra que las curvas y 2 = 4x y x 2 + y 2 − 6x + 1 = 0 se tocan en el punto (1, 2).
Solución:
Tenemos,
y2 = 4x. . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2y (dy/dx) = 4
=> m 1 = dy/dx = 2/y
También tenemos,
X 2 + y 2 – 6x + 1 = 0 . . . . (2)
Derivando ambos con respecto a x, obtenemos,
=> 2x + 2y (dy/dx) − 6 = 0
=> m 2 = dy/dx = (6−2x)/2y = (3−x)/y
En x = 1 y y = 2, tenemos,
metro 1 = 2/2 = 1
metro2 = (3−1)/2 = 1.
Como m 1 = m 2 , podemos decir que las curvas se tocan en (1, 2).
Por lo tanto probado.
Pregunta 8. Encuentra la condición para que las siguientes curvas se corten ortogonalmente:
(i) x 2 /a 2 − y 2 /b 2 = 1 y xy = c 2
Solución:
Tenemos,
x 2 /a 2 − y 2 /b 2 = 1
Derivando ambos lados con respecto a x, obtenemos,
=> 2x/a 2 − (2y/b 2 ) (dy/dx) = 0
=> m 1 = dy/dx = b 2 x/a 2 y
Además, xy = c 2
Derivando ambos lados con respecto a x, obtenemos,
=> y + x (dy/dx) = 0
=> m 2 = dy/dx = −y/x
Para que las curvas se crucen ortogonalmente, m 1 m 2 = −1.
=> (b 2 x/a 2 y) (−y/x) = −1
=> un 2 = segundo 2
Por lo tanto, a 2 = b 2 es la condición para que las curvas se corten ortogonalmente.
(ii) x 2 /a 2 + y 2 /b 2 = 1 y x 2 /A 2 − y 2 /B 2 = 1
Solución:
Tenemos,
x 2 /a 2 + y 2 /b 2 = 1 . . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x/a 2 + (2y/b 2 ) (dy/dx) = 0
=> m 1 = dy/dx = −b 2 x/a 2 y
Además, x 2 /A 2 − y 2 /B 2 = 1 . . . . (2)
=> 2x/A 2 − (2y/B 2 ) (dy/dx) = 0
=> m 2 = dy/dx = B 2 x/A 2 y
Para que las curvas se crucen ortogonalmente, m 1 m 2 = −1.
=> (−b 2 x/a 2 y) (B 2 x/A 2 y) = −1
=> X 2 /y 2 = un 2 UN 2 /b 2 segundo 2 . . . . (3)
Restar (2) de (1) da,
=>
=>
Poniendo este valor en (3), obtenemos,
=>
=> segundo 2 + segundo 2 = un 2 − UN 2
=> un 2 – segundo 2 = UN 2 + segundo 2
Por lo tanto, a 2 − b 2 = A 2 + B 2 es la condición para que las curvas se corten ortogonalmente.
Pregunta 9. Demuestra que las curvas 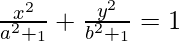 y se
y se 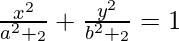 intersecan en ángulos rectos.
intersecan en ángulos rectos.
Solución:
Tenemos,
. . . . (1)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x/(a 2 + λ 1 ) + 2y/(b 2 + λ 1 ) (dy/dx) = 0
=> m 1 = dy/dx =
También tenemos,
. . . . (2)
Derivando ambos lados con respecto a x, obtenemos,
=> 2x/(a 2 + λ 2 ) + 2y/(b 2 + λ 2 ) (dy/dx) = 0
=> m 2 = dy/dx =
Para que las curvas se crucen ortogonalmente, m 1 m 2 = −1.
=>
=>
. . . . (3)
Restar (2) de (1) da,
=>
=>
Poniendo este valor en (3), obtenemos,
=>
=> metro 1 metro 2 = −1
Por lo tanto probado.
Pregunta 10. Si la recta x cos α + y sen α = p toca la curva x 2 /a 2 − y 2 /b 2 = 1, entonces demuestre que a 2 cos 2 α − b 2 sen 2 α = p 2 .
Solución:
Supongamos que (x 1 , y 1 ) es el punto donde la línea recta x cos α + y sen α = p toca la curva
x 2 /a 2 − y 2 /b 2 = 1.
Ahora la ecuación de la tangente a x 2 /a 2 − y 2 /b 2 = 1 en (x 1 , y 1 ) será,
=>
Por tanto, la ecuación
y la recta x cos α + y sen α = p representan la misma recta. Entonces, obtenemos,
=>
=> x 1 = a 2 (cos α)/p y x 2 = b 2 (sen α)/p . . . . (1)
Ahora el punto (x 1 , y 1 ) se encuentra en la curva x 2 /a 2 − y 2 /b 2 = 1.
=>
Usando (1), obtenemos,
=>
=> un 2 cos 2 α − segundo 2 pecado 2 α = pag 2
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA