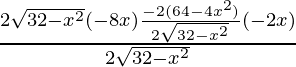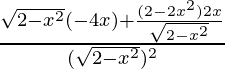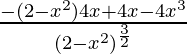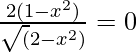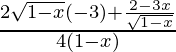Clase 12 Soluciones RD Sharma – Capítulo 18 Máximos y Mínimos – Ejercicio 18.3

Pregunta 1. Encuentre los puntos de máximos locales o mínimos locales y los valores máximos locales y mínimos locales correspondientes de la siguiente función. Además, encuentre los puntos de inflexión, si los hay:

(i) f(x) = x ⁴ – 62x ² + 120x + 9

Solución:

Función dada: f(x) = x ⁴ – 62x ² + 120x + 9

Derivando con respecto a x

f'(x) = 4x ³ – 124x + 120 = 4(x ³ – 31x + 30)

Nuevamente derivando con respecto a x

f”(x) = 12x ² – 124 = 4(3x ² – 31)

Ahora, para máximos y mínimos.

Pon f'(x) = 0

⇒ 4(x ³ – 31x + 30) = 0

⇒ x3 ^– 31x + 30 = 0

⇒ x = 5, 1, -6

Ahora,

f”(5) = 176 > 0

⇒ x = 5 es el punto de los mínimos locales

f”(1) = -112 < 0

⇒ x = 1 es el punto de los máximos locales

f”(-6) = 308 > 0

⇒ x = -6 es el punto de mínimos locales

Ahora, encontramos el valor máximo local = f(1) = 68

y valor mínimo local = f(5) = -316

y = f(-6) = -1647

(ii) f(x) = x ³ – 6x ² + 9x + 15

Solución:

Función dada: f(x) = x ³ – 6x ² + 9x +15

Derivando con respecto a x

f'(x) = 3x ² -12x + 9 = 3(x ² – 4x + 3)

Nuevamente derivando con respecto a x

f”(x) = 6x – 12

Ahora, para máximos y mínimos.

Pon f'(x) = 0

⇒ 3(x ² – 4x + 3) = 0

⇒ x2 – 4x ⁺ 3 = 0

⇒ (x – 3)(x – 1) = 0

⇒ x = 3, 1

Ahora,

f”(3) = 6 > 0

⇒ x = 3 es el punto de los mínimos locales

f”(1) = -6 < 0

⇒ x = 1 es el punto de los máximos locales

⇒ x = -6 es el punto de mínimos locales

Ahora encontramos el valor máximo local = f(1) =19

y valor mínimo local = f(3) = 15

(iii) f(x) = (x – 1)(x + 2) ²

Solución:

Función dada: f(x) = (x – 1)(x + 2) ²

Derivando con respecto a x

f'(x) = (x + 2) ² + 2(x – 1)(x + 2)

= (x + 2)(x + 2 + 2x – 2)

= (x + 2)(3x)

Nuevamente derivando con respecto a x

f”(x) = 3(x+2) + 3x

= 6x + 6

Para máximos y mínimos

Pon f'(x) = 0

⇒ 3x(x + 2) = 0

⇒ x = 0, -2

Ahora,

f”(0) = 6 > 0

⇒ x = 0 es el punto de mínimos locales

f”(-2) = -6 < 0

⇒ x = -2 es el punto de los máximos locales

Ahora encontramos el valor máximo local = f(-2) =0

Valor mínimo local = f(0) = -4

(iv) f(x) = 2/x – 2/x ² , x > 0

Solución:

Función dada: f(x) = 2/x – 2/x ² , x > 0

Derivando con respecto a x

f'(x) = -2/x ² + 4/x ³

Nuevamente derivando con respecto a x

f”(x) = -4/x3 ^–¹² /x4

Para máximos y mínimos

Pon f'(x) = 0

⇒ -2/x2 ⁺ 4/x3 ⁼ 0

⇒ -2(x – 2)/x3 ⁼ 0

⇒ x = 2

Ahora,

f”(2) = 4/8 – 12/6 = 1/2 – 3/4 = -1/4 < 0

⇒ x = 2 es el punto de los máximos locales

Ahora, valor máximo local = f(2) = 1/2

(v) f(x) = xe ^x

Solución:

Función dada: f(x) = xe ^x

Derivando con respecto a x

f'(x) = e ^x + xe ^x = e ^x (x + 1)

Nuevamente derivando con respecto a x

f”(x) = e ^x (x + 1) + e ^x = e ^x (x + 2)

Para máximos y mínimos

Pon f'(x) = 0

⇒ e ^x (x + 1) = 0

⇒ x = -1

Ahora,

f”(-1) = e ^-1 = 1/e > 0

⇒ x = -1 es el punto de los mínimos locales

Ahora, valor mínimo local = f(-1) = -1/e

(vi) f(x) = x/2 + 2/x, x > 0

Solución:

Función dada: f(x) = x/2 + 2/x, x > 0

Derivando con respecto a x

f'(x) = 1/2 – 2/x ²

Nuevamente derivando con respecto a x

f”(x) = 4/x ³

Para máximos y mínimos

Pon f'(x) = 0

⇒ 1/2 – 2/x2 ⁼ 0

⇒ (x2 – 4)/ ^2×2 = ⁰

⇒ x = -2, +2

Ahora,

f”(2) = 4/8 = 1/2 > 0

Por lo tanto, x = 2

x=-2 no se toma porque se da x > 0.

Ahora, valor mínimo local = f (2) = 2

(vii) f(x) = (x + 1)(x + 2) ^1/3 , x ≥ -2

Solución:

Función dada: f(x) = (x + 1)(x + 2) ^1/3 , x ≥ -2

Derivando con respecto a x

f'(x) = (x + 2) ^1/3 + 1/3(x + 1)(x + 2) ^-2/3

= (x + 2) ^-2/3 (x + 2 + 1/3 (x + 1))

= 1/3(x + 2) ^-2/3 (4x + 7)

Nuevamente derivando con respecto a x

f”(x) = -2/9(x + 2) ^-5/3 (4x + 7) + 1/3(x + 2) ^-2/3 × 4

Para máximos y mínimos

Pon f'(x) = 0

⇒ 1/3(x + 2) ^-2/3 (4x + 7) = 0

⇒ (4x + 7) = 0

⇒ x = -7/4

Ahora,

f “(-7/4) = 4/3(-7/4 + 2) ^-2/3

Por lo tanto, x = -7/4 es el punto de los mínimos locales

Ahora, valor mínimo local = f(-7/4) = $\frac{-3}{4^\frac{4}{3}}$

(viii) f(x) = x $\sqrt{32-x^2}$ , -5 ≤ x ≤ 5

Solución:

Función dada: f(x)=x $\sqrt{32-x^2}$ , -5 ≤ x ≤ 5

Derivando con respecto a x

f'(x) = $\sqrt{32-x^2}+\frac{x}{2\sqrt{32-x^2}}$ × (-2x)

= $\frac{2(32-x^2)-2x^2}{2\sqrt{32-x^2}}$

= $\frac{64-4x^2}{2\sqrt{32-x^2}}$

Nuevamente derivando con respecto a x

f”(x) = $\frac{2\sqrt{32-x^2}×(-8x)\frac{-2(64-4x^2)}{2\sqrt{32-x^2}}×(-2x)}{2\sqrt{32-x^2}}$

= $\frac{-4(32-x^2)8x+4x(64-x^2)}{8(32-x^2)^\frac{3}{2}}$

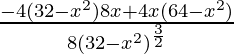
Para máximos y mínimos

Pon f'(x) = 0

⇒ $\frac{64-4x^2}{2\sqrt{32-x^2}}$ = 0

⇒ 64 – 4x ² = 0

⇒ x = ±4

Ahora,

f”(4) = $\frac{-4(32-16)32+16(64-16)}{8(32-16)^{3/2}}$ <0

Por lo tanto, x = 4 es el punto de máximos

Ahora, valor máximo local = f(4) = 16

x = -4 es el punto de mínimos

Ahora, valor mínimo local = f(-4) = -16

(ix) f(x) = x ³ – 2ax ² + a ² x, a > 0, x ∈ R

Solución:

Función dada: f(x) = x ³ – 2ax ² + a ² x

Derivando con respecto a x

f'(x) = 3x ² – 4ax + a ²

Nuevamente derivando con respecto a x

f”(x) = 6x – 4a

Para máximos y mínimos

Pon f'(x) = 0

⇒ 3x ² – 4ax + a ² = 0

⇒ x = $\frac{4a&pm;\sqrt{16a^2-12a^2}}{6}$

= (4a ± 2a)/6 = a, a/3

Ahora,

f”(a) = 2a > 0 cuando a > 0

x = a es el punto de los mínimos locales

f”(a/3) = -2a < 0 como a < 0

x = a/3 es el punto de los máximos locales

Por eso,

El valor máximo local = f(a/3) = ^4a 3/27

y valor mínimo local = f(a) = 0

(x) f(x) = x + a ² /x, a > 0, x ≠ 0

Solución:

Función dada: f(x) = x + a ² /x

Derivando con respecto a x

f'(x) = 1 – a ² /x ²

Nuevamente derivando con respecto a x

f”(x) = 2a ² /x ³

Para máximos y mínimos

Pon f'(x) = 0

⇒ 1 – a ² /x ² = 0

⇒ x ² – un ² = 0

x = ± un

Ahora,

f”(a) = 2/a > 0 cuando a > 0

x = a es el punto de mínimos

f”(-a) = -2/a < 0 cuando a > 0

x = -a es el punto de máximos

Por lo tanto, el valor máximo local = f(-a) = -2a

y valor mínimo local = f(a) = 2a

(xi) f(x) = 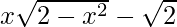$x\sqrt{2-x^2} -\sqrt{2}$ , −√2 ≤ x ≤ √

Solución:

Función dada: f(x) = $x\sqrt{2-x^2}$

Derivando con respecto a x

f'(x) = $\sqrt{2-x^2} -\frac{2x^2}{x\sqrt{2-x^2} }$

= $\frac{2(2-x^2)-2x^2}{2\sqrt{2-x^2}}$

= $\frac{2-2x^2}{\sqrt{2-x^2}}$

Nuevamente derivando con respecto a x

f”(x) = $\frac{\sqrt{2-x^2}(-4x)+\frac{(2-2x^2)2x}{\sqrt{2-x^2}}}{(\sqrt{2-x^2})^2}$

= $\frac{-(2-x^2)4x+4x-4x^3}{(2-x^2)^\frac{3}{2}}$

Para máximos y mínimos

Pon f'(x) = 0

⇒ $\frac{2(1-x^2)}{\sqrt(2-x^2)}=0$

⇒x = ±1

Ahora,

f”(1) < 0

⇒ x = 1 es el punto de los máximos locales

f”(-1) > 0

⇒ x = -1 es el punto de los máximos locales

Por lo tanto, el valor máximo local = f (1) = 1

y valor mínimo local = f (-1) = -1

(xii) 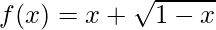$f(x) = x+ \sqrt{1-x}$ , x ≤ 1

Solución:

Función dada: f(x) = x + $\sqrt{1-x}$

Derivando con respecto a x

f'(x) = $1-\frac{1}{2\sqrt{1-x}}=\frac{2\sqrt{1-x}-1}{2\sqrt{1-x}}$

f'(x) = $\frac{2\sqrt{1-x}(\frac{-1}{\sqrt{1-x}})+\frac{2\sqrt{1-x}-1}{\sqrt{1-x}}}{4(1-x)}$

Para máximos y mínimos

Pon f'(x) = 0

⇒ $\frac{2\sqrt{1-x}-1}{2\sqrt{1-x}}=0$

⇒ $\sqrt{1-x}$ =1/2

⇒ x= 1 – 1/4 = 3/4

Ahora,

f”(3/4) < 0

⇒ x = 3/4 es el punto de los máximos locales

Por lo tanto, el valor máximo local = f (3/4) = 5/4

Pregunta 2. Encuentra los valores extremos locales de las siguientes funciones:

(i) f (x) = (x – 1)(x – 2) ²

Solución:

Función dada: f(x) = (x – 1)(x – 2) ²

Derivando con respecto a x

f'(x) = (x – 2) ² + 2(x – 1)(x – 2)

= (x – 2)(x – 2 + 2x – 2)

= (x – 2)(3x – 4)

Nuevamente derivando con respecto a x

f”(x) =(3x – 4) + 3(x – 2)

Para máximos y mínimos

Pon f'(x) = 0

⇒ (x – 2)(3x – 4) = 0

⇒ x = 2, 4/3

Ahora,

f”(2) > 0

x = 2 es mínimos locales

f “(4/3) = -2 < 0

x = 4/3 es el punto de los máximos locales

Por lo tanto, el valor máximo local = f(4/3) = 4/27

y el valor mínimo local = f(2) =0

(ii) f (x) = x $\sqrt{1-x}$ , x ≤ 1

Solución:

Función dada: f (x) = x $\sqrt{1-x}$

Derivando con respecto a x

f'(x) = $\sqrt{1-x}+\frac{x}{2\sqrt{1-x}}(-1)$

= $\frac{2(1-x)-x}{2\sqrt{1-x}}$

= (2 – 3x)/2 $\sqrt{1-x}$

Nuevamente derivando con respecto a x

f”(x) = $\frac{2\sqrt{1-x}(-3)+\frac{2-3x}{\sqrt{1-x}}}{4(1-x)}$

Para máximos y mínimos

Pon f'(x) = 0

⇒ (2 – 3x)/2 $\sqrt{1-x}$ =0

⇒ x = 2/3

Ahora,

f “(2/3) < 0

x = 2/3 es el punto de máximos

Por lo tanto, el valor máximo local = f (2/3) = 2/3√3

(iii) f(x) = -(x – 1) ³ (x + 1) ²

Solución:

Función dada: f(x) = -(x – 1) ³ (x + 1) ²

Derivando con respecto a x

f ‘(x) = -3(x – 1) ² (x + 1) ² – 2(x – 1) ³ (x + 1)

= -(x – 1) ² (x + 1) (3x + 3 + 2x – 2)

= -(x – 1) ² (x + 1) (5x + 1)

Nuevamente derivando con respecto a x

f”(x) = -2(x – 1) (x + 1) (5x + 1) – (x – 1) ² (5x + 1) – 5 (x – 1) ² (x + 1)

Para máximos y mínimos

Pon f'(x) = 0

⇒ -(x – 1) ² (x + 1) (5x + 1) = 0

⇒ x = 1, -1, -1/5

Ahora,

f”(1) = 0

x = 1 es el punto de inflexión

f “(-1) = -4 × -4 = 16 > 0

x = -1 es el punto de mínimos

f”(-1/5) = -5(36/25) × (4/5) = -144/25 < 0

x = -1/5 es el punto de máximos

Por lo tanto, el valor máximo local = f (-1/5) = 3456/3125

y el valor mínimo local = f (-1) = 0

Pregunta 3. La función y = a log x + bx ² + x tiene valores extremos en x = 1 y x = 2. Encuentra a y b.

Solución:

Tenemos,

y = alogx + bx ² + x

Derivando con respecto a x

dy/dx = a/x + 2bx + 1

Nuevamente derivando con respecto a x

d ² y/dx ² = -a/x ² +2b

Para máximos y mínimos

Ponga dy/dx = 0

⇒ a/x + 2bx +1 = 0

Dado que el valor extremo existe en x = 1, 2

⇒ a + 2b = -1 …..(yo)

a/2 + 4b = -1

⇒ a + 8b = -2 …..(ii)

Al resolver las ecuaciones (i) y (ii), obtenemos

a = -2/3, b = -1/6

Pregunta 4. Demuestre que (log x / x) tiene un valor máximo en x = e.

Solución:

Función dada: f(x) = logx / x

Derivando con respecto a x

f'(x) $=\frac{x(1/x)-logx}{x^2}=\frac{1-logx}{x^2}$

Ahora, f'(x) = 0

⇒ 1 – logx = 0

⇒ logx = 1

⇒ logx = logaritmo

⇒ x = mi

Nuevamente derivando con respecto a x

$f ''(x)=\frac{x^2(-1/x)-(1-logx)(2x)}{x^4}$

$=\frac{-x-2x(1-logx)}{x^4}$

= $\frac{-3+2logx}{x^3}$

Ahora, f”(e) = $\frac{-3+2loge}{e^3}$

=(-3 + 2)/e ³ = -1/e ³ < 0

Por lo tanto, por la prueba de la segunda derivada, f es el máximo en x = e.

Pregunta 5. Encuentra los valores máximo y mínimo de la función f (x) = 4/(x + 2) + x.

Solución:

Función dada: f(x) = 4/(x + 2) + x

Derivando con respecto a x

f'(x) = -4/(x + 2) ² + 1

Nuevamente derivando con respecto a x

f”(x) = 8/(x + 2) ³

Para máximos y mínimos

Pon f'(x) = 0

⇒ -4/(x + 2) ² + 1 = 0

⇒ (x + 2) ² = 4

⇒x2 + 4x = ⁰

⇒ x (x + 4) = 0

x = 0, -4

Ahora,

f”(0) = 1 > 0

x = 0 es el punto de mínimos

f”(-4) = -1 < 0

x = -4 es el punto de máximos

Por lo tanto, el valor máximo local = f (-4) = -6

y el valor mínimo local = f (0) = 2

Pregunta 6. Encuentra los valores máximo y mínimo de f (x) = tan x – 2x.

Solución:

Función dada: f(x) = tanx – 2x

Derivando con respecto a x

f'(x) = segundo ² x – 2

Nuevamente derivando con respecto a x

f”(x) = 2seg ² x tanx

Para máximos y mínimos

Pon f'(x) = 0

⇒ sexo ² x = 2

⇒ secx = ±√2

⇒ x = π/4, 3π/4

f”(π/4) = 4 > 0

x = π/4 es el punto de mínimos

f”(3π/4) = -4 < 0

x = (3π/4) es el punto de máximos

Por lo tanto, el valor máximo = f (3π/4) = -1 – 3π/2

y el valor mínimo = f (π/4) = 1 – π/2

Pregunta 7. Si f(x) = x ³ + ax ² + bx + c tiene un máximo en x = -1 y un mínimo en x = 3. Determina a, b y c.

Solución:

Función dada: f(x) = x ³ + ax ² + bx + c

Derivando con respecto a x

f'(x) = 3x ² + 2ax + b

Se da que f(x) es máxima en x = -1

f'(-1) = 3(-1) ² + 2a(-1) + b = 0

f'(-1) = 3 – 2a + b = 0 …….(i)

En x = 3, f(x) es mínimo

f'(3) = 3(3) ² + 2a(3) + b = 0

⇒ f ‘(3) = 27 + 6a +b = 0 …..(ii)

Al resolver las ecuaciones (i) y (ii), obtenemos

a = -3 y b = -9

Dado que f ‘(x) es independiente de la constante c, entonces, puede ser cualquier número real.

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentre los puntos de máximos locales o mínimos locales y los valores máximos locales y mínimos locales correspondientes de la siguiente función. Además, encuentre los puntos de inflexión, si los hay:

(i) f(x) = x 4 – 62x 2 + 120x + 9

(ii) f(x) = x 3 – 6x 2 + 9x + 15

(iii) f(x) = (x – 1)(x + 2) 2

(iv) f(x) = 2/x – 2/x 2 , x > 0

(v) f(x) = xe x

(vi) f(x) = x/2 + 2/x, x > 0

(vii) f(x) = (x + 1)(x + 2) 1/3 , x ≥ -2

(viii) f(x) = x , -5 ≤ x ≤ 5

(ix) f(x) = x 3 – 2ax 2 + a 2 x, a > 0, x ∈ R

(x) f(x) = x + a 2 /x, a > 0, x ≠ 0

(xi) f(x) = , −√2 ​≤ x ≤ √

(xii) , x ≤ 1

Pregunta 2. Encuentra los valores extremos locales de las siguientes funciones:

(i) f (x) = (x – 1)(x – 2) 2

(ii) f (x) = x , x ≤ 1

(iii) f(x) = -(x – 1) 3 (x + 1) 2

Pregunta 3. La función y = a log x + bx 2 + x tiene valores extremos en x = 1 y x = 2. Encuentra a y b.

Pregunta 5. Encuentra los valores máximo y mínimo de la función f (x) = 4/(x + 2) + x.

Pregunta 6. Encuentra los valores máximo y mínimo de f (x) = tan x – 2x.

Pregunta 7. Si f(x) = x 3 + ax 2 + bx + c tiene un máximo en x = -1 y un mínimo en x = 3. Determina a, b y c.

Deja una respuesta Cancelar la respuesta

(i) f(x) = x ⁴ – 62x ² + 120x + 9

(ii) f(x) = x ³ – 6x ² + 9x + 15

(iii) f(x) = (x – 1)(x + 2) ²

(iv) f(x) = 2/x – 2/x ² , x > 0

(v) f(x) = xe ^x

(vii) f(x) = (x + 1)(x + 2) ^1/3 , x ≥ -2

(viii) f(x) = x $\sqrt{32-x^2}$ , -5 ≤ x ≤ 5

(ix) f(x) = x ³ – 2ax ² + a ² x, a > 0, x ∈ R

(x) f(x) = x + a ² /x, a > 0, x ≠ 0

(xi) f(x) = $x\sqrt{2-x^2} -\sqrt{2}$ , −√2 ≤ x ≤ √

(xii) $f(x) = x+ \sqrt{1-x}$ , x ≤ 1

(i) f (x) = (x – 1)(x – 2) ²

(ii) f (x) = x $\sqrt{1-x}$ , x ≤ 1

(iii) f(x) = -(x – 1) ³ (x + 1) ²

Pregunta 3. La función y = a log x + bx ² + x tiene valores extremos en x = 1 y x = 2. Encuentra a y b.

Pregunta 7. Si f(x) = x ³ + ax ² + bx + c tiene un máximo en x = -1 y un mínimo en x = 3. Determina a, b y c.