Clase 12 Soluciones RD Sharma – Capítulo 18 Máximos y mínimos – Ejercicio 18.4

Pregunta 1. Encuentre los valores máximo absoluto y mínimo absoluto de las siguientes funciones en los intervalos dados:

(i) f(x) = 4x – x ² /2 pulgadas [-2, 9/2]

Solución:

Dado: f(x) = 4x – x ² /2 en [-2, 9/2]

En la diferenciación, obtenemos,

f'(x) = 4 – x

Para máximos locales y mínimos locales tenemos f'(x) = 0

4 – x = 0

⇒ x = 4

Evaluemos el valor de f en el punto crítico x=4 y en el intervalo [-2, 9/2]

f(4) = 4(4) – 4 ² /2 = 16 – 16/2 = 16 – 8 = 8

f(-2) = 4(-2) – (-2) ^2/2 = -8 – 4/2 = -8 – 2 = -10

f(9/2) = 4(9/2) – (9/2) ² /2 = 18 – 81/8 = 18 –

Por lo tanto, el valor máximo absoluto de f en [-2, 9/2] es 8 en x = 4 y

el valor mínimo absoluto de f en [-2, 9/2] es -10 en x = -2.

(ii) f(x) = (x – 1) ² +3 en [-3, 1]

Solución:

Dado: f(x) = (x – 1) ² +3 en [-3, 1]

En la diferenciación, obtenemos,

f'(x) = 2(x – 1)

Para máximos locales y mínimos locales tenemos f'(x) = 0

Evaluemos el valor de f en el punto crítico x = 1 y en el intervalo [-3, 1]

Por lo tanto, el valor máximo absoluto de f en [-3, 1] es 19 en x = -3 y

el valor mínimo absoluto de f en [-3, 1] es 3 en x = 1.

(iii) f(x) = 3x ⁴ – 8x ³ + 12x ² – 48x + 25 en [0, 3]

Solución:

Dado: f(x) = 3x ⁴ – 8x ³ + 12x ² – 48x + 25 en [0,3]

En la diferenciación, obtenemos,

Ahora, para mínimos locales y máximos locales tenemos

x = 2 o sin raíces reales

por lo que consideramos sólo

Evaluemos el valor de f en el punto crítico x = 2 y en el intervalo

Por lo tanto, el valor máximo absoluto de f en es 25 en x = 0 y

el valor mínimo absoluto de f en es -39 en x = 2.

(iv) 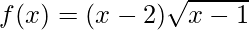$f(x)=(x-2) \sqrt{x-1}$ en [1, 9]

Solución:

dado: $f(x)=(x-2) \sqrt{x-1}$ en

En la diferenciación, obtenemos,

$f'(x) = \sqrt{x-1} + \frac {x-2} {2\sqrt {x-1}}$

Ahora, para mínimos locales y máximos locales tenemos

$\sqrt{x-1} + \frac {x-2} {2\sqrt {x-1}}=0$

= $\frac {2(x-1) + {x-2}} {2\sqrt {x-1}}=0$

= $\frac {3x-4} {2\sqrt {x-1}}=0$

= x = 4/3

Evaluemos el valor de f en el punto crítico x = 4/3 y en el intervalo [1, 9]

$f(1)=(1-2)\sqrt {1-1}=(-1)\sqrt {0}=0$

$f(\frac 4 3)= (\frac 4 3 -2)\sqrt {\frac 4 3 -1}=\frac {4-6} {3\sqrt3}=\frac {-2} {3\sqrt3}=\frac {-2\sqrt3} 9$

$f(9)=(9-2)\sqrt{9-1}=7\sqrt8=14\sqrt2$

Por lo tanto, el valor máximo absoluto de f en [1, 9] es 14√2 en x = 9 y

el valor mínimo absoluto de f en [1, 9] está $\frac {-2\sqrt3} 9$ en x = 4/3

Pregunta 2. Encuentra el valor máximo de 2x ³ – 24x + 107 en el intervalo [1, 3]. Encuentre el valor máximo de la misma función en [-3, -1].

Solución:

Sea f(x) = 2x ³ – 24x + 107

∴ f'(x) = 6x ² – 24 = 6(x ² – 4)

Ahora, para máximos locales y mínimos locales tenemos

6(x ² – 4) = 0

× ² = 4

x = ±2

Primero consideramos el intervalo [1, 3].

f(2) = 2(2) ³ – 24(2) + 107 = 75

f(1) = 2(1) ³ – 24(1) + 107 = 85

f(3) = 2(3) ³ – 24 (3) + 107 = 89

.

f(−3) = 2(-3) ³ – 24(-3) + 107 = 125

f(-2) = 2(-2) ³ – 24(-3) + 107 = 139

f(-1) = 2(-1) ³ – 24(-2) + 107 = 129

Por lo tanto, el valor máximo absoluto de f es 139 cuando x = -2.

Pregunta 3. Encuentra los valores máximos y mínimos absolutos de la función f dada por f(x) = cos ² x + senx, x ∈ [0, ].

Solución:

Dado: f(x) = cos ² x + senx, x ∈ [0, ]

En la diferenciación, obtenemos,

Ahora, para mínimos locales y máximos locales tenemos

x ∈ [0, ]

Evaluemos el valor de f en los puntos críticos x = nd en el intervalo [0, ]

f(π/6) = cos ² π/6 + senπ/6 = (√3/2) ² +1/2 =

Por lo tanto, el valor máximo absoluto de fi

Pregunta 4. Encuentra los valores absolutos máximo y mínimo de la función f dada por f(x) = 12x ^4/3 – 6x ^1/3 , x ∈ [−1, 1].

Solución:

Dado: f(x) = 12x ^4/3 – 6x ^1/3 , x ∈ [−1, 1].

En la diferenciación, obtenemos,

$f'(x)=16x^{\frac 1 3}-\frac 2 {x^{\frac 2 3}}=\frac {2(8x-1)} {x^{\frac 2 3}}$

Ahora, para mínimos locales y máximos locales tenemos

$\frac {2(8x-1)} {x^{\frac 2 3}}=0$

⇒ x = 1/8

Evaluemos el valor de f en los puntos críticos x = 1/8 y en el intervalo [-1, 1]

f(1/8) = 12(1/8) ^4/3 – 6(1/8) ^1/3 = -9/4

^4/3^1/3

^4/3^1/3

Por lo tanto, el valor máximo absoluto de f en [-1, 1] es 18 en x = -1 y

el valor mínimo absoluto de f en [-1, 1] es -9/4 en x = 1/8.

Pregunta 5. Encuentra los valores máximos y mínimos absolutos de la función f dada por f(x) = 2x ³ – 15x ² + 36x + 1 en el intervalo [1, 5].

Solución:

Dado: f(x) = 2x ³ – 15x ² + 36x + 1 en el intervalo [1, 5]

En la diferenciación, obtenemos,

Ahora, para mínimos locales y máximos locales tenemos

Evaluemos el valor de f en los puntos críticos x = 2 y x = 3 y en el intervalo [1, 5]

f(1) = 2(1) ³ – 15(1) ² + 36(1) + 1 = 24

f(2) = 2(2) ³ – 15(2) ² + 36(2) + 1 = 29

f(3) = 2(3) ³ – 15(3) ² + 36(3) + 1 = 28

f(5) = 2(5) ³ – 15(5) ² + 36(5) + 1 = 56

Por lo tanto, el valor máximo absoluto de f en [1, 5] es 56 en x = 5 y

el valor mínimo absoluto de f en [1, 5] es 24 en x = 1.

Publicación traducida automáticamente

Artículo escrito por manandeep1610 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentre los valores máximo absoluto y mínimo absoluto de las siguientes funciones en los intervalos dados:

(i) f(x) = 4x – x 2 /2 pulgadas [-2, 9/2]

(ii) f(x) = (x – 1) 2 +3 en [-3, 1]

(iii) f(x) = 3x 4 – 8x 3 + 12x 2 – 48x + 25 en [0, 3]

(iv) en [1, 9]

Pregunta 2. Encuentra el valor máximo de 2x 3 – 24x + 107 en el intervalo [1, 3]. Encuentre el valor máximo de la misma función en [-3, -1].

Pregunta 3. Encuentra los valores máximos y mínimos absolutos de la función f dada por f(x) = cos 2 x + senx, x ∈ [0, ].

Pregunta 4. Encuentra los valores absolutos máximo y mínimo de la función f dada por f(x) = 12x 4/3​ – 6x 1/3 ​, x ∈ [−1, 1].

Pregunta 5. Encuentra los valores máximos y mínimos absolutos de la función f dada por f(x) = 2x 3 – 15x 2 + 36x + 1 en el intervalo [1, 5].

Deja una respuesta Cancelar la respuesta

(i) f(x) = 4x – x ² /2 pulgadas [-2, 9/2]

(ii) f(x) = (x – 1) ² +3 en [-3, 1]

(iii) f(x) = 3x ⁴ – 8x ³ + 12x ² – 48x + 25 en [0, 3]

(iv) $f(x)=(x-2) \sqrt{x-1}$ en [1, 9]

Pregunta 2. Encuentra el valor máximo de 2x ³ – 24x + 107 en el intervalo [1, 3]. Encuentre el valor máximo de la misma función en [-3, -1].

Pregunta 3. Encuentra los valores máximos y mínimos absolutos de la función f dada por f(x) = cos ² x + senx, x ∈ [0, ].

Pregunta 4. Encuentra los valores absolutos máximo y mínimo de la función f dada por f(x) = 12x ^4/3 – 6x ^1/3 , x ∈ [−1, 1].

Pregunta 5. Encuentra los valores máximos y mínimos absolutos de la función f dada por f(x) = 2x ³ – 15x ² + 36x + 1 en el intervalo [1, 5].